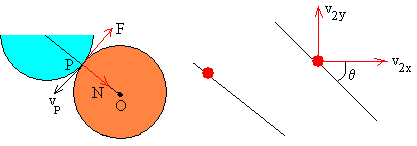
En la figura, se muestra un esquema de la colisión de dos discos de masas m₁ y m₂ y radios r₁ y r₂, respectivamente. El segundo disco está en reposo $\overrightarrow{u_2}=0$ , mientras que el primero lleva una velocidad $\overrightarrow{u_1}$ antes del choque. El choque está caracterizado por el denominado parámetro de impacto b, que es la distancia entre la dirección de la velocidad del primer disco y el centro del segundo disco en reposo.

Después del choque, el primer disco se mueve con velocidad $\overrightarrow{v_1}$ haciendo un ángulo φ₁ con eje horizontal (dirección de la velocidad $\overrightarrow{u_1}$ del disco incidente) y a su vez, gira alrededor de un eje perpendicular al disco y que pasa por su centro, con velocidad angular ω₁. El segundo disco, se mueve con velocidad $\overrightarrow{v_2}$ haciendo un ángulo φ₂ con el eje horizontal y a su vez, gira alrededor de de un eje perpendicular al disco y que pasa por su centro, con velocidad angular ω₂.

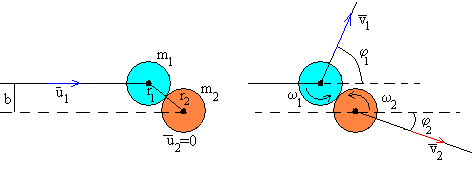
Tenemos que despejar seis incógnitas del sistema de ecuaciones que describe el choque entre dos discos:

• Los módulos de las velocidades de los c.m. de los discos después del choque v₁ y v₂, y sus direcciones φ₁ y φ₂
• Las velocidades angulares de rotación de cada uno de los discos alrededor de un eje perpendicular al disco y que pasa por el c.m. ω₁  y ω₂.

Choques frontales

Los choques frontales son las más fáciles de describir ya que solamente, precisan la aplicación del principio de conservación del momento lineal y la definición de coeficiente de restitución.

m₁u₁ =m₁v₁+m₂v₂           (1)

 -e·u₁=v₁-v_2p                 (2)

${\displaystyle v_1=\frac{(M-e)}{M+1}{u}_1{v}_2=\frac{M(1+e)}{M+1}{u}_{1}M=\frac{m_1}{m_2}}$

Choques oblicuos

Parámetro de impacto

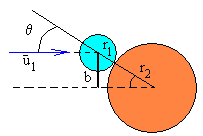
Se denomina parámetro de impacto b, a la distancia entre la dirección de la velocidad u₁ del primer disco y el centro del segundo disco en reposo. Relacionamos el parámetro de impacto b y el ángulo θ que forma la dirección de la velocidad u₁ del primer disco y la recta que pasa por los centros de ambos discos, cuando entran en contacto en el momento del choque, tal como se puede apreciar en la figura.

b=(r₁+r₂)·sinθ

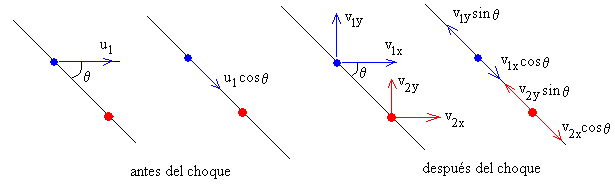
Conservación del momento lineal

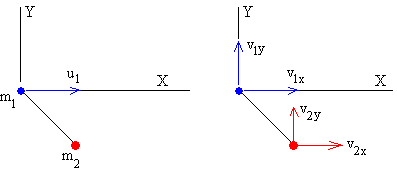
• a lo largo del eje X

m₁u₁ =m₁v_1x+m₂v_2x                (1)

• a lo largo del eje Y

0=m₁v_1y+m₂v_2y                       (2)

Conservación del momento angular

• Se conserva el momento angular del disco 1 respecto del punto de contacto P.



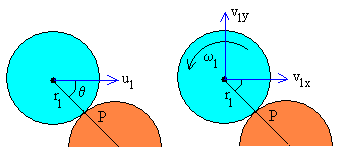
-m₁·r₁·u₁sinθ= I₁ω₁- m₁·r₁·(v_1xsinθ+ v_1ycosθ)                   (3)

• Se conserva el momento angular del disco 2 respecto del punto de contacto P.



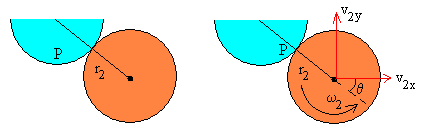
0=I₂ω₂ +m₂·r₂·(v_2xsinθ+ v_2ycosθ)                                    (4)

Balance energético. Coeficiente de restitución

La definición de coeficiente de restitución es

${\displaystyle e=-\frac{(v_{1x}\cos \theta -v_{1y}\text{sin}\theta )-(v_{2x}\cos \theta -v_{2y}\text{sin}\theta )}{u_1\cos \theta }}$                  (5)

Cuando los discos están en contacto

• No hay deslizamiento

Consideremos el caso de que no hay deslizamiento de un disco respecto del otro en el punto de contacto P. Las velocidades de los dos discos en el punto de contacto P serán iguales.



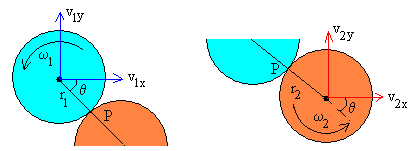
r₁ω₁+v_1xsinθ+ v_1ycosθ= -r₂ω₂ + v_2xsinθ+ v_2ycosθ                     (6)

• Hay deslizamiento



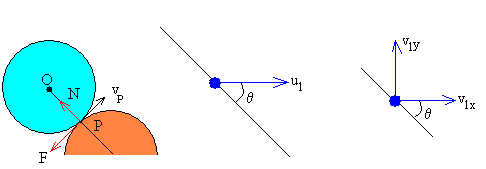
Las fuerzas sobre el disco azul en el punto de contacto son:

• La reacción N,
• La fuerza de rozamiento F

Si las superficie lateral del disco azul desliza sobre la del rojo, la relación entre ambas fuerzas es F=μ·N

La fuerza N actuando durante el pequeño intervalo de tiempo Δt en el que los discos están en contacto modifica la componente del momento lineal del disco en la dirección de dicha fuerza. Lo mismo cabe decir de la fuerza F.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\Delta t}{\int }}N·dt}=(m_1{v}_{1y}\text{sin}\theta -m_1{v}_{1x}\cos \theta )-(-m_1{u}_1\cos \theta )\\ {\displaystyle \underset{0}{\overset{\Delta t}{\int }}-F·dt}=(m_1{v}_{1x}\text{sin}\theta +m_1{v}_{1y}\cos \theta )-m_1{u}_1\text{sin}\theta \end{array}}$

μ(v_1ysinθ-v_1xcosθ+u₁cosθ)=- v_1xsinθ-v_1ycosθ+u₁sinθ              (6)

Las fuerzas sobre el disco rojo en el punto de contacto son:

• La reacción N,
• La fuerza de rozamiento F

iguales y de sentido contrario a las que se ejercen sobre el disco azul.



${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\Delta t}{\int }}N·dt}=(m_2{v}_{2x}\text{cos}\theta -m_2{v}_{2y}\text{sin}\theta )\\ {\displaystyle \underset{0}{\overset{\Delta t}{\int }}F·dt}=(m_2{v}_{2x}\text{sin}\theta +m_2{v}_{2y}\cos \theta )\end{array}}$

μ(v_2xcosθ-v_2ysinθ)=v_2xsinθ+v_2ycosθ                                    (7)

Resolución del sistema de ecuaciones

Llamamos M=m₁/m₂

El momento de inercia de un sólido rígido en rotación alrededor de un eje fijo es

I=kmr² con k=1/2 para un disco

El sistema de seis ecuaciones con seis incógnitas se escribe.

Mv_1x+v_2x= Mu₁+u₂         (1)

Mv_1y+v_2y=0                      (2)

v_1xsinθ+ v_1ycosθ-kr₁ω₁= u₁sinθ            (3)

v_2xsinθ+ v_2ycosθ +kr₂ω₂ =0                     (4)

-v_1xcosθ + v_1ysinθ+v_2xcosθ-v_2ysinθ=eu₁cosθ           (5)

v_1xsinθ+ v_1ycosθ - v_2xsinθ-v_2ycosθ +r₁ω₁+r₂ω₂ =0      (6)   No desliza

(- μcosθ+sinθ)v_1x+(μsinθ +cosθ) v_1y=u₁(sinθ- μcosθ)   (6) Desliza

Para resolver el sistema de ecuaciones lineales, cambiamos el orden de las ecuaciones para evitar que los elementos de la diagonal de la matriz cuadrada (más abajo) sean nulos

• No desliza

v_1xsinθ+ v_1ycosθ - v_2xsinθ- v_2ycosθ +r₁ω₁+r₂ω₂ =0      (6)  
Mv_1y+v_2y=0                                                                       (2)
Mv_1x+v_2x= Mu₁+u₂                                                           (1)
-v_1xcosθ + v_1ysinθ+v_2xcosθ-v_2ysinθ=eu₁cosθ                  (5)
v_1xsinθ+ v_1ycosθ-kr₁ω₁= -u₁sinθ                                     (3)
v_2xsinθ+ v_2ycosθ +kr₂ω₂=0                                              (4)

En forma matricial escribimos el sistema

${\displaystyle \left(\begin{array}{cccccc}\text{sin}\theta & \cos \theta & \text{-sin}\theta & -\cos \theta & 1& 1\\ 0& M& 0& 1& 0& 0\\ M& 0& 1& 0& 0& 0\\ -\cos \theta & \text{sin}\theta & \cos \theta & -\text{sin}\theta & 0& 0\\ \text{sin}\theta & \cos \theta & 0& 0& -k& 0\\ 0& 0& \text{sin}\theta & \cos \theta & 0& k\end{array}\right)\left(\begin{array}{c}{v}_{1x}\\ v_{1y}\\ v_{2x}\\ v_{2y}\\ r_1{\omega }_1\\ r_2{\omega }_2\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ M{u}_1\\ e{u}_1\cos \theta \\ u_1\text{sin}\theta \\ 0\end{array}\right)}$

Se resuelve el sistema de ecuaciones se evalúa el primer y segundo miembro de la ecuación (6) caso "desliza"

A=μ(v_1ysinθ-v_1xcosθ+u₁cosθ)
B=- v_1xsinθ-v_1ycosθ+u₁sinθ

Si A>B se mantiene el resultado, en caso contrario se resuelve el sistema alternativo

• Desliza

(- μcosθ+sinθ)v_1x+(μsinθ +cosθ) v_1y=u₁(sinθ- μcosθ)    (6)
Mv_1y+v_2y=0                                                                       (2)
Mv_1x+v_2x= Mu₁+u₂                                                           (1)
-v_1xcosθ + v_1ysinθ+v_2xcosθ-v_2ysinθ=eu₁cosθ                  (5)
v_1xsinθ+ v_1ycosθ-kr₁ω₁= -u₁sinθ                                     (3)
v_2xsinθ+ v_2ycosθ +kr₂ω₂ =0                                              (4)

En forma matricial escribimos el sistema

${\displaystyle \left(\begin{array}{cccccc}\text{-}\mu \text{cos}\theta +\text{sin}\theta & \mu \text{sin}\theta +\cos \theta & 0& 0& 0& 0\\ 0& M& 0& 1& 0& 0\\ M& 0& 1& 0& 0& 0\\ -\cos \theta & \text{sin}\theta & \cos \theta & -\text{sin}\theta & 0& 0\\ \text{sin}\theta & \cos \theta & 0& 0& -k& 0\\ 0& 0& \text{sin}\theta & \cos \theta & 0& k\end{array}\right)\left(\begin{array}{c}{v}_{1x}\\ v_{1y}\\ v_{2x}\\ v_{2y}\\ r_1{\omega }_1\\ r_2{\omega }_2\end{array}\right)=\left(\begin{array}{c}{u}_1(\text{sin}\theta -\mu \cos \theta )\\ 0\\ M{u}_1\\ e{u}_1\cos \theta \\ u_1\text{sin}\theta \\ 0\end{array}\right)}$

Comprobamos que la solución es correcta en este caso, verificándose la ecuación

μ(v_2xcosθ-v_2ysinθ)=v_2xsinθ+v_2ycosθ                       (7)

Procedimiento de cálculo

Llamamos M a la matriz, X al vector columna de las incógnitas y B al vector columna de los términos independientes

M·X=B

Despejamos el vector columna de las incógnitas

X=M^-1·B

M^-1 es la matriz inversa de M. En sintaxis de MATLAB

X=M\B

M=1; %cociente m1/m2 entre las masas de los discos
u1=3.5; %velocidad inicial del primer disco (el segundo en reposo)
e=0.94; %coeficiente de restitución
mu=0.1; %coeficiente de rozamiento
ang=48.6*pi/180; %ángulo incidente 
k=0.5; %momento de inercia de los discos (1/2)mr^2
if ang==0   %choques frontales
     v1=(M-e)*u1/(1+M);
     v2=M*(1+e)*u1/(1+M);
     fi1=.0;
     fi2=0.0;
     w1=0.0;
     w2=0.0;    
else
    matriz=[[sin(ang), cos(ang), -sin(ang), -cos(ang), 1, 1];
        [0, M, 0, 1, 0, 0];
        [M, 0, 1, 0, 0, 0];
        [-cos(ang), sin(ang), cos(ang), -sin(ang),0, 0];
        [sin(ang), cos(ang), 0, 0, -k, 0];
        [0, 0, sin(ang), cos(ang), 0, k]];    
    
    vector=[0,0,M*u1, e*u1*cos(ang),u1*sin(ang),0]';
    solucion=matriz\vector;
   
    V1x=solucion(1);
    V1y=solucion(2);
    V2x=solucion(3);
    V2y=solucion(4);
    w1=solucion(5);
    w2=solucion(6);
    A=mu*(V1y*sin(ang)-(V1x-u1)*cos(ang));
    B=u1*sin(ang)-V1x*sin(ang)-V1y*cos(ang);
    if A<B
          matriz(1,1)=sin(ang)-mu*cos(ang);
          matriz(1,2)=cos(ang)+mu*sin(ang);
          matriz(1,3)=0;
          matriz(1,4)=0;
          matriz(1,5)=0;
          matriz(1,6)=0;
          vector(1)=-mu*u1*cos(ang)+u1*sin(ang);
          solucion=matriz\vector;
          V1x=solucion(1);
          V1y=solucion(2);
          V2x=solucion(3);
          V2y=solucion(4);
          w1=solucion(5);
          w2=solucion(6);
    end
    v1=sqrt(V1x*V1x+V1y*V1y);
    fi1=atan2(V1y,V1x);
    v2=sqrt(V2x*V2x+V2y*V2y);
    fi2=atan2(V2y,V2x);
end
Q=M*v1*v1/2+M*k*w1*w1/2+v2*v2/2+k*w2*w2/2-M*u1*u1/2;
fprintf('Disco 1: velocidad v1=%1.3f, rotación w1=%1.3f, 
ángulo fi1=%2.2f\n',v1,w1,fi1*180/pi)  
fprintf('Disco 2: velocidad v2=%1.3f, rotación w2=%1.3f, 
ángulo fi2=%2.2f\n',v2,w2,fi2*180/pi)
fprintf('Energía perdida Q=%1.3f\n',Q)

Disco 1: velocidad v1=2.402, rotación w1=-0.449, ángulo fi1=39.74
Disco 2: velocidad v2=2.256, rotación w2=-0.449, ángulo fi2=-42.89
Energía perdida Q=-0.594

Ejemplo

Comprobaremos,  la conservación del momento lineal y del momento angular de los discos, a partir de los datos suministrados por el programa interactivo.

Datos relativos a los discos

• Las masas de los discos, m₁=1, m₂=1, por lo que M=m₁/m₂=1
• Los radios de los discos  r₁=1,  r₂=1
• Discos ambos de acero, e=0.94 y μ =0.10

Antes del choque

• Velocidad inicial u₁=3.5 del primer disco
• Parámetro de impacto b=1.5, por lo que sinθ=1.5/(1+1), θ=48.60º

Después del choque

• Velocidad del primer disco v₁=2.40, dirección φ₁=39.75º (por encima de la horizontal)
• Velocidad del segundo disco v₂=2.26, dirección φ₂=-42.88º (por debajo de la horizontal)
• Velocidad angular del primer disco r₁·ω₁=-0.45, o bien ω₁=-0.45 (gira en el sentido de las agujas del reloj)
• Velocidad angular del segundo disco r₂·ω₂=-0.45, o bien ω₂=-0.45

1. Conservación del momento lineal



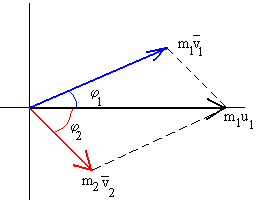
El momento lineal inicial del primer disco (el segundo está inicialmente en reposo) es igual a la suma vectorial de los momentos lineales de los discos después del choque.

m₁u₁=m₁v₁cosφ₁+m₂v₂cosφ₂
0=m₁v₁sinφ₁+m₂v₂sinφ₂

• Antes del choque

Eje X: 1·3.5=3.5
Eje Y: 0.0

• Después del choque

Eje X: 1·2.40·cos39.75+1·2.26·cos(-42.88)=3.49
Eje Y: 1·2.40·sin39.75+2·2.26·sin(-42.88)=0.003≈ 0.0

El momento lineal se conserva

2. Conservación del momento angular

• Se conserva el momento angular del disco 1 respecto del punto de contacto P.



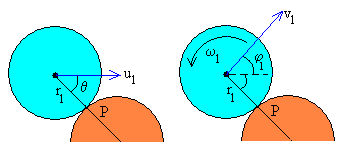
-m₁·r₁·u₁sinθ= I₁ω₁- m₁·r₁·v₁sin(θ+φ₁)
-1·1·3.5·sin48.60=1·1²·(-0.45)/2-1·1·2.40·sin(48.60+39.75)

(Las velocidades angulares son positivas en el sentido contrario al de las agujas del reloj)

• Se conserva el momento angular del disco 2 respecto del punto de contacto P.



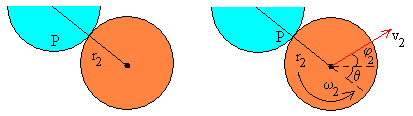
0=I₂ω₂ +m₂·r₂·v₂sin(θ+φ₁) 
0=1·1²·(-0.45)/2-1·1·2.26·sin(48.60+-42.88)

3. Balance energético

Energía inicial $E_i=\frac{1}{2}{m}_1{u}_1^2$

E_i=6.125

Energía final $E_f=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2+\frac{1}{2}{I}_1{\omega }_1^2+\frac{1}{2}{I}_2{\omega }_2^2$

E_f=5.535

Energía perdida en la colisión Q=E_f-E_i=-0.590

Ejemplo 2º Choques frontales

Datos relativos a los discos

• Masas de los discos m₂=1, m₁=0.5, por lo que M=m₁/m₂=0.5
• Discos ambos de acero, e=0.94

Antes del choque

• Velocidad inicial u₁=3.5 del primer disco
• Parámetro de impacto b=0.0, por lo que θ=0º

Después del choque

• Velocidad del primer disco v₁=-1.03
• Velocidad del segundo disco v₂=2.26,

1. Conservación del momento lineal
• Antes del choque

Eje X: 1.3.5=3.5

• Después del choque

Eje X: -1·1.03+2·2.26=3.49

Se conserva el momento lineal

2. Balance energético

Antes del choque

${\displaystyle E_i=\frac{1}{2}0.5·{3.5}^2=3.062}$

Después del choque

${\displaystyle E_f=\frac{1}{2}0.5·{1.03}^2+\frac{1}{2}1·{2.26}^2=2.819}$

Energía perdida en la colisión Q=E_f-E_i=-0.243