${\displaystyle \overrightarrow{M_{ext}}=\frac{d\overrightarrow{L}}{dt}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

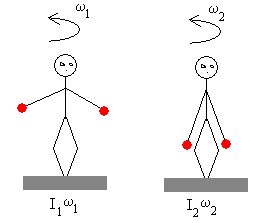
Para un sólido rígido que gira alrededor de un eje principal de inercia $\overrightarrow{L}=I\overrightarrow{\omega }$ .

El aumento de la velocidad angular se explica por la disminución del momento de inercia.

El principio de conservación del momento angular para el patinador se escribe I₁·ω₁=I₂·ω₂

Como el momento de inercia I₂<I₁ por estar los brazos  más cerca del eje de rotación del cuerpo, la velocidad angular se incrementa ω₂>ω₁.

Conservación del momento angular

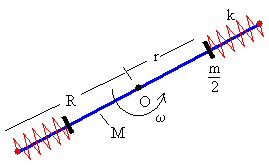
En la figura, vemos el sistema formado por

• Una varilla rígida delgada de masa M y longitud 2R

• Dos masas deslizantes iguales de masa m/2 cada una

• Dos muelles elásticos iguales de constante k, que se han construido de modo que su longitud sin deformar es igual a R. Cada muelle se sujeta a un extremo de la varilla, el otro se une a la masa deslizante.

Inicialmente, el sistema gira alrededor del eje que pasa por O, con velocidad angular constante ω₀. Un dispositivo mantiene sujetas las dos masas deslizantes a una distancia r₀ del eje. Vamos a determinar la velocidad angular de rotación cuando se liberan las dos masas deslizantes.

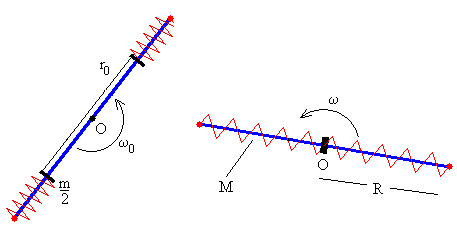
El momento angular inicial es

${\displaystyle L=\left(I_v+m{r}_0^2\right){\omega }_0}$

• el primer término entre paréntesis I_v, es el momento de inercia de la varilla I_v=M(2R)²/12= MR²/3,

• el segundo término, es el momento de inercia de las dos masas iguales m/2 que distan r₀ del eje de rotación.

El momento angular final, cuando las dos masas deslizantes se encuentran en el origen r=0, es

L=I_v·ω

Al disminuir el momento de inercia, aumenta la velocidad angular de rotación ω>ω₀.

${\displaystyle \omega =\frac{I_v+m{r}_0^2}{I_v}{\omega }_0}$

Movimiento de las masas deslizantes

Vamos a estudiar el movimiento de las dos masas deslizantes, desde el estado inicial al final.

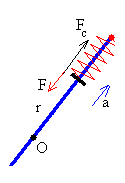
Nos situamos en el Sistema de Referencia no inercial que gira con la varilla con velocidad angular ω. Sobre cada una de las masas (m/2), situadas a una distancia r del eje de rotación, se ejercen las siguientes fuerzas:

• El muelle que está comprimido ejerce una fuerza F=-k·r

• La fuerza centrífuga F_c=(m/2)ω²r.

Bajo la acción de estas fuerzas la masa m/2 experimenta una aceleración a en la dirección radial, a lo largo de la varilla

La segunda ley de Newton se escribe

${\displaystyle \frac{m}{2}a=\frac{m}{2}{\omega }^{2}r-kr}$

Ahora bien, la velocidad angular de rotación ω, no es constante, su dependencia con r se obtiene de la conservación del momento angular L=(I_v+mr²)ω,

${\displaystyle \frac{m}{2}a=\frac{m}{2}\frac{L^2}{{(I_v+m{r}^2)}^2}r-kr}$

La ecuación diferencial que describe el movimiento de una masa en la dirección radial, es decir, en el Sistema de Referencia que se mueve con la varilla es

${\displaystyle \frac{d^{2}r}{d{t}^2}=\frac{r{L}^2}{{(I_v+m{r}^2)}^2}-\frac{2k}{m}r}$

Integramos esta ecuación diferencial mediante procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, la velocidad radial de la masa dr/dt=0, y su distancia al eje r=r₀.

r0=0.8; %posicón inicial de las masas deslizantes
w0=1;  %velocidad angular inicial
m=0.5; %masa de los dos bloques
Iv=1/12; %momento de inercia de la varilla
k=1; %constante del muelle
L=(m*r0*r0+Iv)*w0; %momento angular
x0=zeros(1,2);
x0(1)=r0;  %posición de partida
x0(2)=0;
f=@(t,x) [x(2);x(1)*L^2/(Iv+m*x(1)^2)^2-2*k*x(1)/m]; 
tspan=[0 4];
[t,x]=ode45(f,tspan,x0);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('r');
title('Posición radial en función del tiempo')
figure
plot(t,w0*(Iv+m*r0^2)./(Iv+m*x(:,1).^2))
grid on
xlabel('t')
ylabel('\omega');
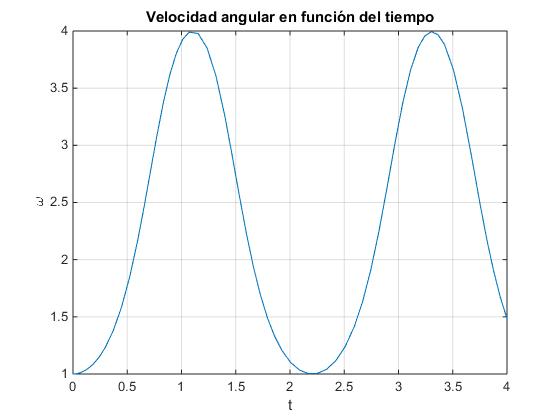
title('Velocidad angular en función del tiempo')

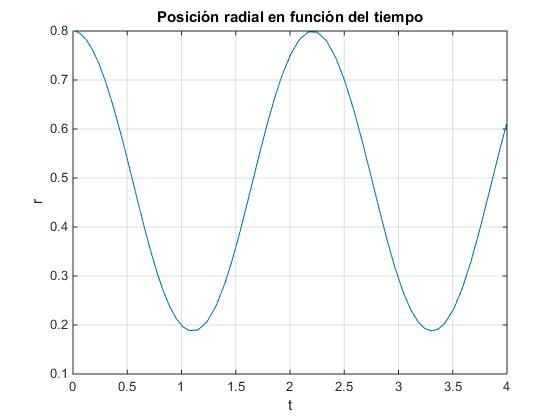
Conocida la distancia r de las masas deslizantes al eje de rotación en el instante t, se calcula la velocidad angular ω de rotación sabiendo que el momento angular L permanece constante.

${\displaystyle \left(I_v+m{r}^2\right)\omega =\left(I_v+m{r}_0^2\right){\omega }_0}$

Curvas de energía potencial

La energía inicial del sistema, cuando las masas se encuentran sujetas, es la suma de

• la energía cinética de las dos masas que se mueven con velocidad tangencial ω₀·r₀.

• la energía cinética de rotación de la varilla que se mueve con velocidad angular ω₀

• la energía elástica almacenada en los dos muelles comprimidos r₀.

La suma de los dos primeros términos, es la energía cinética de rotación del sistema formado por la varilla y las dos masas.

${\displaystyle E=2·\left(\frac{1}{2}\frac{m}{2}{\omega }_0^2{r}_0^2\right)+\frac{1}{2}{I}_v{\omega }_0^2+2\left(\frac{1}{2}k{r}_0^2\right)=\frac{1}{2}(m{r}_0^2+I_v){\omega }_0^2+k{r}_0^2}$

Cuando se liberan las dos masas y se encuentran a una distancia r del eje de rotación. La energía del sistema formado por la varilla, las dos masas y los dos muelles elásticos iguales, se escribe en coordenadas polares

${\displaystyle E=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)+\frac{1}{2}{I}_v{\omega }^2+k{r}^2}$

• El primer término, es la energía cinética de las dos masas, que consta  a su vez de dos términos:

• La primera derivada dr/dt es la velocidad en la dirección radial, la velocidad de la masa que desliza a lo largo de la varilla;

• La segunda derivada, es la velocidad en la dirección tangencial dθ/dt=ω, que es la velocidad angular de rotación de la varilla.

• El segundo término, es la energía cinética de rotación de la varilla

• El tercer término, es la energía elástica almacenada en los dos muelles

Teniendo en cuanta que el momento angular es constante, expresamos la energía E del sistema en función de r y de su derivada dr/dt,

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}(m{r}^2+I_v)\frac{L^2}{{(I_v+m{r}^2)}^2}+k{r}^2=\\ \frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}\frac{L^2}{I_v+m{r}^2}+k{r}^2\end{array}}$

Dividimos la energía E entre las dos masas iguales, podemos considerar que cada una de ellas se mueve en un potencial efectivo

${\displaystyle V_{ef}(r)=\frac{1}{4}\frac{L^2}{I_v+m{r}^2}+\frac{1}{2}k{r}^2}$

La fuerza resultante sobre cada una de las masas se obtiene derivando la energía potencial y cambiando de signo.

${\displaystyle f(r)=-\frac{d{V}_{ef}(r)}{dr}=\frac{m}{2}\frac{L^2}{{(I_v+m{r}^2)}^2}r-kr=\frac{m}{2}{\omega }^{2}r-kr}$

que como vemos es la diferencia entre la fuerza centrífuga y la fuerza que ejerce el muelle comprimido.

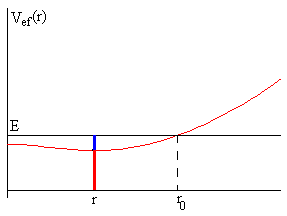
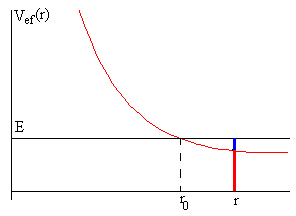
En la figura, tenemos la representación del potencial efectivo de las dos masas que salen de la posición inicial r₀, con velocidad radial dr/dt=0. Si su energía total es E (recta horizontal), las masas llegan al origen r=0 al cabo de un cierto tiempo.

Cuando las masas están a una distancia r del origen, se representa mediante un segmento vertical rojo su energía potencial efectiva y mediante un segmento de color azul, la energía cinética correspondiente a su movimiento en la dirección radial, a lo largo de la varilla.

Observaremos que la velocidad angular de rotación ω, crece hasta que se hace máxima cuando las masas se pegan al eje.

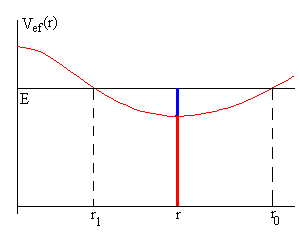
En la figura, tenemos una situación distinta, las masas salen de la posición inicial r₀, con velocidad radial dr/dt=0. Si su energía total es E, no alcanzan el eje de rotación, sino que se aproximan al mismo a una distancia r₁, cambian el sentido de la velocidad, se alejan del eje hasta que alcanzan la posición inicial de partida y así, continúan oscilando en la dirección radial.

Observaremos que la velocidad angular de rotación ω, crece hasta que se hace máxima cuando las masas se acercan al eje y luego, disminuye cuando se alejan del eje.

Calculamos la distancia r₁ poniendo dr/dt=0 en la expresión de la energía total E. Obtenemos una ecuación de cuarto grado en r que reducimos a una ecuación de segundo grado, cuyas soluciones son r₀ y r₁. Véase el ejemplo 2 más abajo.

Si la constante elástica, k es pequeña y las masas son grandes, cuando se liberan, se mueven alejándose del eje central hasta que llegan a los extremos de la varilla.

Ejemplos

Ejemplo 1:

• Masa de los dos bloques, m=0.5 kg

• Constante de cada muelle, k=1 N/m

• Distancia inicial al eje de rotación, r₀=0.6 m

• El momento de inercia de la varilla, I_v=1/12 kg·m²

• La velocidad angular inicial de rotación, ω₀= 1 rad/s

Observamos que al cabo de un cierto tiempo, las masas se quedan pegadas al eje de rotación

• El momento angular inicial es

L=(1/12+0.5·0.6²)·1=0.263 kg·m²/s

• El momento angular final es

L=(1/12)·ω

La velocidad angular final de rotación es ω=3.16 rad/s

Ejemplo 2:

Con los mismos datos del ejemplo anterior, cambiamos el momento angular, variando la distancia al eje de rotación de las dos masas r₀=0.9.

• El momento angular inicial es

L=(1/12+0.5·0.9²)·1=0.488 kg·m²/s

La energía del sistema formado por las dos masas, la varilla y los dos muelles es

${\displaystyle E=\frac{1}{2}(m{r}_0^2+I_v){\omega }_0^2+k{r}_0^2=\frac{1}{2}\left(0.5·{0.9}^2+\frac{1}{12}\right)·1^2+1·{0.9}^2=1.05\text{J}}$

Las dos masas se mueven hacia el origen, pero retroceden cambiando el sentido de su velocidad radial cuando se encuentran a la distancia r₁ que se calcula poniendo dr/dt=0 en la expresión de la energía total E en función de r.

${\displaystyle E=\frac{1}{2}\frac{L^2}{I_v+m{r}^2}+k{r}^2}$

Después de algunas operaciones, nos queda la ecuación

2mkr⁴+2(I_vk-mE)r²+L²-2I_vE=0

Con los datos de este ejemplo

r⁴-0.8875r²+0.0628=0

Sustituyendo x=r² tenemos una ecuación de segundo grado cuyas raíces son x₁=0.81, y x₂=0.0775, o sus correspondientes r₁=0.9, y r₂=0.28.

• La velocidad angular ω de rotación es máxima para r=0.28 m

L=(1/12+0.5·0.28²)·ω 

de la constancia del momento angular se obtiene ω=3.98 rad/s

Ejemplo 3:

• Masa de los dos bloques, m=2 kg

• Constante de cada muelle, k=0.2 N/m

• Distancia inicial al eje de rotación, r₀=0.6 m

Observamos que las dos masas se alejan del eje, hasta que llegan a los extremos de la varilla.

• El momento angular inicial es

L=(1/12+2·0.6²)·1=0.803 kg·m²/s

• El momento angular final para r=1 m

L=(1/12+2·1²)·ω

La velocidad angular final de rotación es menor que la inicial ω=0.39 rad/s

Actividades

Se introduce

• La masa m de los dos bloques en kg, en el control titulado Masa bloques.

• La constante elástica k de cada uno de los muelles en N/m, en el control titulado Cte. Muelle.

• La posición inicial r₀ de las dos masas, su distancia al eje de rotación, en el control titulado Posición bloques.

• El momento de inercia de la varilla delgada se ha fijado en I_v=1/12 kgm²

• La velocidad inicial de rotación se ha fijado en ω₀=1 rad/s

Se pulsa el botón titulado Nuevo.

Observamos la rotación del sistema, con velocidad angular ω₀=1 rad/s, las dos masas están separadas una distancia r₀ del eje de rotación mediante un dispositivo.

A la derecha, se representa la energía potencial efectiva V_ef(r) y la energía total E del sistema mediante una recta horizontal. La curva y la recta se encuentran en el punto de abscisa r₀.

Se pulsa el botón titulado Libera

Observamos el movimiento de las masas a lo largo de la varilla. En la parte superior izquierda, se proporciona los datos de sus distancias al eje y de la velocidad angular de rotación ω del sistema.

Referencias

Kalotas T. M. Lee A.R.. A simple device to illustrate angular momentum conservation and instability. Am. J. Phys. 58 (1) January 1990, pp. 80-81