Caída de una bola que gira sobre sí misma.
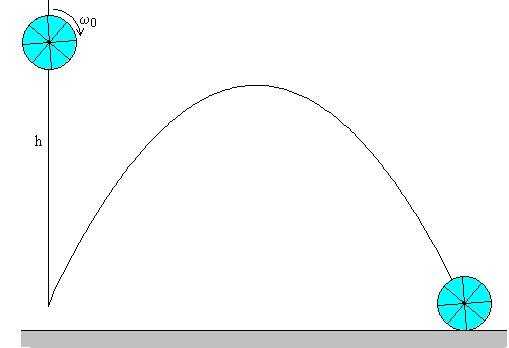
Caída de la bola
El centro de masas de la bola desciende una altura h, como consecuencia su velocidad al llegar al suelo y=0 es
Choque de la bola con el suelo
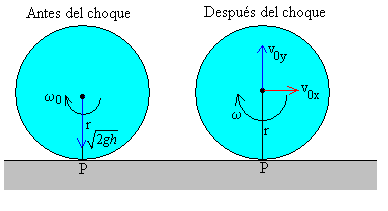
La bola antes del choque tiene una velocidad:
- angular de rotación, ω0
- de traslación de su c.m.,
Después del choque la bola tendrá una
- Velocidad angular de rotación, ω
- Las componentes de la velocidad de traslación de su c.m. serán: v0x y v0y
Coeficiente de restitución
De la definición de coeficiente de restitución e obtenemos la componente v0y de la velocidad después del choque vale
Conservación del momento angular
Como las fuerzas que ejerce la pared sobre bola actúan en el punto de contacto P. El momento de dichas fuerzas respecto de P es cero. El momento angular respecto de dicho punto será constante.
Para una bola de radio r y momento de inercia I=2mr2/5.
- El momento angular inicial respecto de P es
- El momento angular final respecto de P
-Iω0
-Iω-mv0xr
La conservación del momento angular se escribe
Iω0 =Iω+mv0xr
Fuerzas sobre la bola
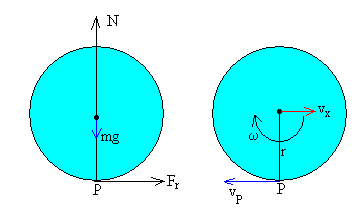
Las fuerzas sobre la bola en el momento del choque son:
- La reacción del suelo N
- El peso mg que es muy pequeño comparado con N, tal como se explicó en la página anterior.
- La fuerza de rozamiento que se opone a la velocidad del punto P de contacto de la bola con el suelo, como consecuencia disminuirá la velocidad de rotación ω e incrementará la velocidad vx de traslación del c.m.
vP=vx-ωr
La bola permanece en contacto con el suelo un tiempo pequeño Δt. Al final de este intervalo de tiempo pueden ocurrir dos casos:
- La bola rueda sin deslizar
- La bola desliza
- La reacción N actuando durante un intervalo de tiempo Δt, modifica la componente vertical de la velocidad de la bola.
- La fuerza de rozamiento Fr actuando durante un intervalo de tiempo Δt, modifica la componente horizontal de la velocidad de la bola.
Para que le bola ruede sin deslizar, la velocidad del punto P de contacto de la bola con el suelo deberá ser nula.
v0x= ωr
De la conservación del momento angular
Iω0 =Iω+mωr2
Las velocidades finales después del choque son
Si la fuerza de rozamiento no tiene tiempo suficiente para establecer el equilibrio entre rotación y traslación, es decir, vP<0, el punto de contacto P desliza sobre el suelo.
Como el punto P desliza sobre el suelo, Fr=μN
Llegamos a la relación
De la conservación del momento angular
Iω0 =Iω+mv0xr
Para que esta solución sea válida se tiene que cumplir que vP<0, es decir que ωr>v0x
Balance energético del choque entre la bola y el suelo rígido
La energía cinética inicial de la bola es
La energía cinética final de la bola es
En el primer caso,
En el segundo caso
Tiro parabólico
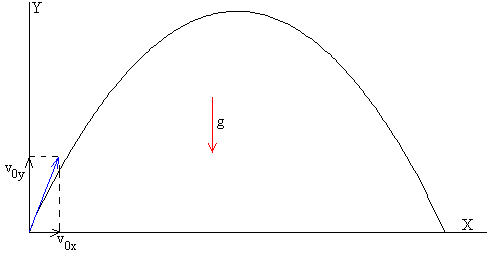
Una vez que la bola ha chocado con el suelo, describe una trayectoria parabólica. Las ecuaciones del movimiento son.
La altura máxima se calcula con vy=0
El alcance se calcula con y=0. Hay dos posibles resultados, dependiendo del valor de v0x
Ejemplos
Ejemplo 1.
- Coeficiente de rozamiento, μ=0.1
- Coeficiente de restitución, e=0.9
- Velocidad angular inicial de rotación, ω0=30 rad/s
- Radio de la esfera, r=0.1 m
- Altura de caída, h=1.0 m
Calculamos las componentes de la velocidad después del choque y la velocidad angular de rotación.
La componente vertical vale
Calculamos la velocidad angular inicial crítica
Como ω0>ω0c la componente horizontal de la velocidad v0x y la velocidad angular de rotación ω valen, respectivamente,
El alcance es
Ejemplo 2.
- Cambiamos la velocidad angular inicial de rotación, ω0=20 rad/s
Como ω0<ω0c la bola al final del choque rueda sin deslizar, la velocidad del punto de contacto P con el suelo es vP=0. La componente horizontal de la velocidad v0x y la velocidad angular de rotación ω valen, respectivamente
El alcance es
Actividades
Se introduce
- El coeficiente de rozamiento μ, en el control titulado Coef. rozamiento.
- El coeficiente de restitución e, en el control titulado Restitución
- La velocidad angular inicial de rotación de la bola ω0, en el control titulado V. angular.
- Se ha fijado el radio de la bola r=0.1 m=10 cm y la altura de caída del centro de la bola h=1.0 m
Se pulsa el botón titulado Nuevo
El programa interactivo calcula inmediatamente después del choque de la bola con el suelo
- La componente horizontal de la velocidad del c.m. de la bola, v0x
- La componente vertical de la velocidad del c.m. de la bola, v0y
- La velocidad angular de rotación, ω
Podemos observar el movimiento de la bola, medir su alcance y altura máxima. Detenemos la bola en el segundo rebote.

