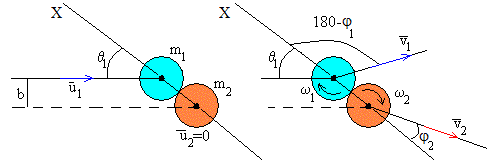
En la figura, se muestra un esquema de la colisión de dos discos de masas m₁ y m₂, y radios r₁ y r₂ respectivamente. El segundo disco está en reposo $\overrightarrow{u_2}=0$ , mientras que el primero lleva una velocidad $\overrightarrow{u_1}$ antes del choque. El choque está caracterizado por el denominado parámetro de impacto b, que es la distancia entre la dirección de la velocidad $\overrightarrow{u_1}$ del primer disco y el centro del segundo disco en reposo. Alternativamente, podemos caracterizarla por el ángulo θ₁ que forma la dirección de la velocidad $\overrightarrow{u_1}$ del primer disco y la recta (eje X) que pasa por los centros de ambos discos cuando entran en contacto en el momento del choque.

Después del choque, el primer disco se mueve con velocidad $\overrightarrow{v_1}$ haciendo un ángulo φ₁ con la parte positiva del eje X y a su vez, gira alrededor de un eje perpendicular al disco y que pasa por su centro con velocidad angular ω₁. El segundo disco se mueve con velocidad $\overrightarrow{v_2}$ haciendo un ángulo φ₂ con el eje X y a su vez, gira alrededor de de un eje perpendicular al disco y que pasa por su centro con velocidad angular ω₂.

Datos del problema

• Las masas de los discos m₁ y m₂ y sus radios r₁ y r₂
• La velocidad inicial u₁ del primer disco y su dirección θ₁. El segundo disco está en reposo $$\overrightarrow{u_2}=0$$

Incógnitas

• La velocidad del centro del primer disco después del choque v₁, su dirección φ₁, la velocidad angular de rotación ω_1.
• La velocidad del centro del segundo disco después del choque v₂, su dirección φ₂, la velocidad angular de rotación ω_2.

Parámetro de impacto

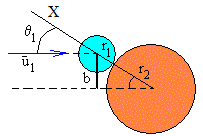
Se denomina parámetro de impacto b, a la distancia entre la dirección de la velocidad $\overrightarrow{u_1}$ del primer disco y el centro del segundo disco en reposo. La relación entre le parámetro de impacto b y el ángulo θ₁ que forma la dirección de la velocidad $\overrightarrow{u_1}$ del primer disco y la recta (eje X) que pasa por los centros de ambos discos, cuando entran en contacto en el momento del choque, se puede apreciar en la figura.

b=(r₁+r₂)·sinθ₁

Principios de conservación

1. Tenemos un sistema aislado de dos partículas interactuantes. Aplicamos el principio de conservación del momento lineal

${\displaystyle \overrightarrow{F_{ext}}=\frac{d\overrightarrow{P}}{dt}\overrightarrow{F_{ext}}=0\overrightarrow{P}=\text{cte}}$

Denominamos eje X a la recta que une los centros de los dos discos cuando entran en contacto en el momento del choque y eje Y a la dirección perpendicular.

En la figura, se han sustituido los vectores $\overrightarrow{u_1},\overrightarrow{v_1},\overrightarrow{v_2}$ por sus componentes a lo largo del eje X y del eje Y



• A lo largo del eje Y

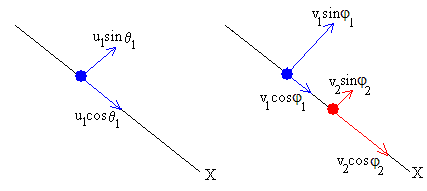
m₁u₁·sinθ₁=m₁v₁·sinφ₁+m₂v₂·sinφ₂                  (1)

• A lo largo del X

m₁u₁·cosθ₁= m₁v₁·cosφ₁+m₂v₂·cosφ₂              (2)

2. Constancia del momento angular de cada uno de los discos. El momento angular respecto del punto de contacto de los dos discos antes y después del choque es el mismo

${\displaystyle \overrightarrow{M_{ext}}=\frac{d\overrightarrow{L}}{dt}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

El momento angular de cada uno de los discos se mantiene constante. Ya que las fuerzas que ejerce un disco sobre el otro actúan en el punto de contacto P. El momento de dichas fuerzas respecto de P es cero.



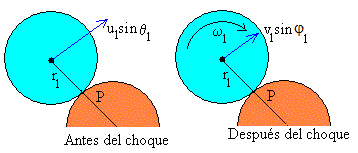
m₁·r₁·u₁sinθ₁=m₁·r₁·v₁sinφ₁+I₁ω₁



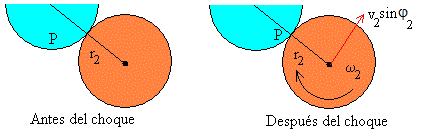
0=-m₂·r₂·v₂sinφ₂+I₂ω₂

Sabiendo que los momentos de inercia de cada uno de los discos respecto al ejes perpendicular al disco y que pasa por su centro son:

${\displaystyle I_1=\frac{1}{2}{m}_1{r}_1^2{I}_2=\frac{1}{2}{m}_2{r}_2^2}$

r₁ω₁ =2·u₁sinθ₁-2·v₁sinφ₁                   (3)
r₂ω₂ =2·v₂sinφ₂                                                (4)

Balance energético. Coeficiente de restitución

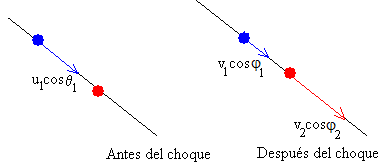
De la definición de coeficiente de restitución

${\displaystyle e=-\frac{v_1\cos {\phi }_1-v_2\cos {\phi }_2}{u_1\cos {\theta }_1}}$

e·u₁cosθ₁= -v₁cosφ₁+v₂cosφ₂                           (5)

Tenemos 6 incógnitas y tan solo 5 ecuaciones, precisamos una ecuación más para resolver el problema. Estudiamos ahora las fuerzas entre los discos cuando entran en contacto

Cuando los discos están en contacto

Supondremos que:

1. Que las fuerzas normales dependen de las propiedades elásticas de los cuerpos, mientras que las fuerzas tangenciales dependen del rozamiento entre los discos, las cuales dependen del estado de las superficies en contacto.
2. Que los coeficientes de restitución y de rozamiento son constantes y solamente dependen de la naturaleza de los materiales con los que están hechos los discos.

Se pueden presentar dos casos:

No hay deslizamiento

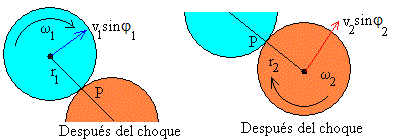
Consideremos el caso de que no hay deslizamiento de un disco respecto del otro en el punto de contacto P. Las velocidades de los dos discos en el punto de contacto P serán iguales.

v₁sinφ₁-r₁ω₁=v₂sinφ₂+r₂ω₂                   (6)

Hay deslizamiento

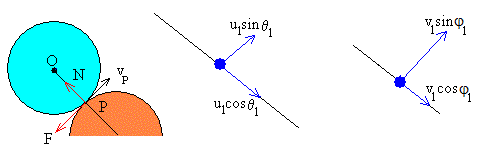
Las fuerzas sobre el disco azul en le punto de contacto son:

• La reacción N,
• La fuerza de rozamiento F

La fuerza N actuando durante el pequeño intervalo de tiempo Δt en el que los discos están en contacto modifica la componente del momento lineal del disco a lo largo de la dirección de dicha fuerza..

${\displaystyle -{\displaystyle \underset{0}{\overset{\Delta t}{\int }}N·dt}=m_1{v}_1\cos {\phi }_1-m_1{u}_1\cos {\theta }_1}$

De modo análogo, el impulso de la fuerza F modifica el momento lineal del disco. La fuerza de rozamiento F es de sentido contrario a la velocidad del disco en el punto de contacto P.

${\displaystyle -{\displaystyle \underset{0}{\overset{\Delta t}{\int }}F·dt}=m_1{v}_1\text{sin}{\phi }_1-m_1{u}_1\text{sin}{\theta }_1}$

De la relación entre ambas fuerzas F=μ·N, obtenemos

μ ·(v₁cosφ₁- u₁cosθ₁)= (v₁sinφ₁-u₁sinθ₁)                (6')

Las fuerzas sobre el disco rojo en el punto de contacto son:

• La reacción N,
• La fuerza de rozamiento F.

Las fuerzas en el punto de contacto P son iguales y de sentido contrario

La fuerza N actuando durante el pequeño intervalo de tiempo Δt en el que los discos están en contacto modifica la componente del momento lineal del disco en la dirección de dicha fuerza.

${\displaystyle {\displaystyle \underset{0}{\overset{\Delta t}{\int }}N·dt}=m_2{v}_2\cos {\phi }_2}$

De modo análogo, el impulso de la fuerza F modifica el momento lineal del disco. La fuerza de rozamiento F es de sentido contrario a la velocidad del disco en el punto de contacto P.

${\displaystyle {\displaystyle \underset{0}{\overset{\Delta t}{\int }}F·dt}=m_2{v}_2\text{sin}{\phi }_2}$

De la relación ente ambas fuerzas F=μ·N, obtenemos

μ ·v₂cos φ₂= v₂sinφ₂                         

tanφ₂ =μ                    (7')

Resolución de las ecuaciones

De los dos casos estudiados hay cinco ecuaciones comunes

m₁u₁·sinθ₁=m₁v₁·sinφ₁+m₂v₂·sinφ₂                (1)
m₁u₁·cosθ₁= m₁v₁·cosφ₁+m₂v₂·cosφ₂              (2)

r₁ω₁ =2·u₁sinθ₁-2·v₁sinφ₁                             (3)
r₂ω₂ =2·v₂sinφ₂                                                             (4)

e·u₁cosθ₁= -v₁cosφ₁+v₂cosφ₂                              (5)

Las ecuaciones específicas

Hay deslizamiento

• La ecuación (7') nos proporciona el ángulo φ₂  que hace la velocidad de la segunda partícula v₂ después del choque con la línea que une los centros de las dos partículas en el momento del choque

tanφ₂ =μ                    (7')

La ecuación (7') se puede escribir de forma alternativa

sinφ₂=μ·cosφ₂       (7')

• El módulo de la velocidad v₁ y el ángulo φ₁ que hace la dirección de dicha velocidad después del choque con la línea que une los centros de las dos partículas en el momento del choque

Se introduce (7') en la ecuación (1), se despeja v₂cosφ₂ de (5) y se sustituye en (1) y (2)

u₁·(m₁sinθ₁-μ ·e·m₂cosθ₁)=m₁v₁·sinφ₁+m₂v₁·μ ·cosφ₁
u₁·(m₁-m₂ ·e)·cosθ₁= (m₁+m₂)v₁·cosφ₁

Llamando M=m₁/m₂, despejamos v₁·cosφ₁ de la ecuación (2) y v₁·sinφ₁ de la ecuación (1)

${\displaystyle \begin{array}{l}{v}_1\text{sin}{\phi }_1=\left(\text{sin}{\theta }_1-\frac{\mu (1+e)}{M+1}\cos {\theta }_1\right)u_1\\ v_1\text{cos}{\phi }_1=\frac{M-e}{M+1}{u}_1\cos {\theta }_1\\ \tan {\phi }_1=\frac{M+1}{M-e}\tan {\theta }_1-\frac{\mu (1+e)}{M-e}\\ v_1^2=u_1^2\left\{{\text{sin}}^2{\theta }_1+{\left(\frac{\mu (1+e)}{M+1}\right)}^2{\cos }^2{\theta }_1-2\frac{\mu (1+e)}{M+1}\text{sin}{\theta }_1\cos {\theta }_1+{\left(\frac{M-e}{M+1}\right)}^2{\cos }^2{\theta }_1\right\}=\\ u_1^2{\cos }^2{\theta }_1\left\{{\tan }^2{\theta }_1+{\left(\frac{\mu (1+e)}{M+1}\right)}^2-2\frac{\mu (1+e)}{M+1}\tan {\theta }_1+{\left(\frac{M-e}{M+1}\right)}^2\right\}\end{array}}$

• Módulo de la velocidad de la segunda partícula v₂ después del choque

Se despeja v₁·cosφ₁ en la ecuación (5) y se sustituye en la ecuación (2)
m₁u₁·cosθ₁= m₁v₁·cosφ₁+m₂v₂·cosφ₂              (2)

${\displaystyle \begin{array}{l}{v}_2\cos {\phi }_2=\frac{m_1(1+e)}{(m_1+m_2)}{u}_1\cos {\theta }_1{v}_2\text{sin}{\phi }_2=\mu v_2\cos {\phi }_2=\frac{m_1(1+e)\mu }{(m_1+m_2)}{u}_1\cos {\theta }_1\\ v_2=\frac{M(1+e)}{(M+1)}\sqrt{1+{\mu }^2}{u}_1\cos {\theta }_1\end{array}}$

• Velocidades angulares de rotación de los discos ω₁ y ω₂

Despejamos v₁·sinφ₁ de la ecuación (1) y la sustituimos en la (3)

r₁ω₁ =2·u₁sinθ₁-2·v₁sinφ₁=2(m₂/m₁)v₂·sinφ₂         (3)

${\displaystyle r_1{\omega }_1=\frac{2\mu (1+e)}{M+1}{u}_1\cos {\theta }_1}$
r₂ω₂ =2·v₂sinφ₂                      (4)

${\displaystyle r_2{\omega }_2=M\frac{2\mu (1+e)}{M+1}{u}_1\cos {\theta }_1}$

Comprobación

No hemos empleado la ecuación (6'), pero comprobaremos que se cumple

μ ·(v₁cosφ₁- u₁cosθ₁)= v₁sinφ₁-u₁sinθ₁                  (6')

Introducimos las expresiones de v₁cosφ₁ y de v₁sinφ₁ previamente deducidas y comprobaremos que se cumple la igualdad.   

Balance energético

Se denomina Q de la colisión a la diferencia entre las energías cinéticas de los discos después del choque, y la energía cinética antes del choque

La energía cinética de los discos después del choque, es la suma de dos términos: la energía cinética de traslación del c.m. del disco y la energía cinética de rotación del disco alrededor de un eje que pasa por el c.m.

${\displaystyle Q=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2+\frac{1}{2}\left(\frac{1}{2}{m}_1{r}_1^2\right){\omega }_1^2+\frac{1}{2}\left(\frac{1}{2}{m}_2{r}_2^2\right){\omega }_2^2-\frac{1}{2}{m}_1{u}_1^2}$

Sustituimos las velocidades después del choque v₁, v₂, ω₁ y ω₂ en función de la velocidad del primer disco antes del choque u₁ y del ángulo θ₁.

${\displaystyle Q=\frac{1}{2}{m}_1{u}_1^2{\cos }^2{\theta }_1\left\{\begin{array}{l}{\left(\frac{M-e}{M+1}\right)}^2+{\tan }^2\theta +{\left(\frac{\mu (1+e)}{M+1}\right)}^2-2\frac{\mu (1+e)}{M+1}\tan \theta +\\ \frac{M{(1+e)}^2}{{(M+1)}^2}(1+{\mu }^2)+2{\left(\frac{\mu (1+e)}{M+1}\right)}^2+2M{\left(\frac{\mu (1+e)}{M+1}\right)}^2-\frac{1}{{\cos }^2{\theta }_1}\end{array}\right\}}$

Utilizando las relaciones sin2θ₁=2sinθ₁·cosθ₁ y 1+tan²θ₁=1/cos²θ₁ y después de varias operaciones algebraicas se llega al siguiente resultado

${\displaystyle Q=-\frac{\mu (1+e)\text{sin}(2{\theta }_1)+\left(1-e^2-3{\mu }^2{(1+e)}^2\right){\cos }^2{\theta }_1}{M+1}\frac{1}{2}{m}_1{u}_1^2}$

No hay deslizamiento

• Módulo de la velocidad de la segunda partícula v₂ después del choque y su dirección φ₂

Se sustituye r₁ω₁ y r₂ω₂  de las ecuaciones (3) y (4) en la ecuación (6) específica para este caso particular

r₁ω₁ =2·u₁sinθ₁-2·v₁sinφ₁                             (3)
r₂ω₂ =2·v₂sinφ₂                                                             (4)
v₁sinφ₁-r₁ ω₁=v₂sinφ₂+r₂ ω₂                              (6)

Introducimos las expresiones de r₁ω₁  y de r₂ω₂  en la ecuación (6)

3v₁sinφ₁-2·u₁sinθ₁=3v₂sinφ₂

Despejamos v₁sinφ₁ de esta ecuación y la sustituimos en la ecuación (1)

m₁u₁·sinθ₁=m₁v₁·sinφ₁+m₂v₂·sinφ₂                  (1)

(m₁/3)u₁·sinθ₁=(m₁+m₂)v₂·sinφ₂

${\displaystyle v_2\text{sin}{\phi }_2=\frac{M}{3(M+1)}{u}_1\text{sin}{\theta }_1}$

Despejamos v₁cosφ₁ de la ecuación (5) y la sustituimos en la ecuación (2)

m₁u₁·cosθ₁= m₁v₁·cosφ₁+m₂v₂·cosφ₂              (2)
e·u₁cosθ₁= -v₁cosφ₁+v₂cosφ₂                               (5)

${\displaystyle v_2\text{cos}{\phi }_2=\frac{(1+e)M}{(M+1)}{u}_1\cos {\theta }_1}$

Estas dos ecuaciones nos dan la velocidad de la segunda partícula después del choque v₂ y su dirección φ₂

${\displaystyle \tan {\phi }_2=\frac{\text{1}}{3(1+e)}\tan {\theta }_1{v}_2=\frac{M}{M+1}{u}_1\sqrt{\frac{1}{9}{\text{sin}}^2{\theta }_1+{(1+e)}^2{\cos }^2{\theta }_1}}$

• Módulo de la velocidad de la primer disco v₁ después del choque y su dirección φ₁

En la ecuación (1) sustituimos v₂·sinφ₂ y despejamos v₁·sinφ₁

${\displaystyle v_1\text{sin}{\phi }_1=\frac{3M+2}{3(M+1)}{u}_1\text{sin}{\theta }_1}$

En la ecuación (2) sustituimos v₂·cosφ₂  y despejamos v₁·cosφ₁

${\displaystyle v_1\cos {\phi }_1=-\frac{M-e}{M+1}{u}_1\cos {\theta }_1}$

Estas dos ecuaciones nos dan la velocidad de la primera partícula después del choque v₁ y su dirección φ₁

$$\begin{gathered} {\displaystyle \tan {\phi }_1=\frac{\text{3}M+\text{2}}{3(M-e)}\tan {\theta }_1 \\ {v}_1=\frac{1}{M+1}{u}_1\sqrt{\frac{{(3M+2)}^2}{9}{\text{sin}}^2{\theta }_1+{(M-e)}^2{\cos }^2{\theta }_1}} \end{gathered}$$

• Velocidades angulares de rotación de los discos ω₁ y ω₂

En las ecuaciones (3) y (4) sustituimos v₁sinφ₁ y v₂sinφ₂  por las expresiones calculadas previamente

${\displaystyle r_1{\omega }_1=\frac{2}{3(M+1)}{u}_1\text{sin}{\theta }_1{r}_2{\omega }_2=\frac{2M}{3(M+1)}{u}_1\text{sin}{\theta }_1}$

Balance energético

Se denomina Q de la colisión a la diferencia entre las energías cinéticas de los discos después del choque, y la energía cinética antes del choque

La energía cinética de los discos después del choque, es la suma de dos términos: la energía cinética de traslación del c.m. del disco y la energía cinética de rotación del disco alrededor de un eje que pasa por el c.m.

${\displaystyle Q=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2+\frac{1}{2}\left(\frac{1}{2}{m}_1{r}_1^2\right){\omega }_1^2+\frac{1}{2}\left(\frac{1}{2}{m}_2{r}_2^2\right){\omega }_2^2-\frac{1}{2}{m}_1{u}_1^2}$

Sustituimos las velocidades después del choque v₁, v₂, ω₁ y ω₂ en función de la velocidad del primer disco antes del choque u₁ y de su dirección θ₁.

$$\begin{gathered} {\displaystyle Q=\frac{1}{2}{m}_1{u}_1^2 \\ \left\{\begin{array}{l}{\left(\frac{3M+2}{3(M+1)}\right)}^2{\text{sin}}^2{\theta }_1+{\left(\frac{M-e}{M+1}\right)}^2{\cos }^2{\theta }_1+\frac{1}{M}{\left(\frac{M}{3(M+1)}\right)}^2{\text{sin}}^2{\theta }_1+\frac{1}{M}{\left(\frac{M(1+e)}{M+1}\right)}^2{\cos }^2{\theta }_1\\ +\frac{1}{2}{\left(\frac{2}{3(M+1)}\right)}^{\text{2}}{\text{sin}}^{\text{2}}{\theta }_1+\frac{1}{2}\frac{1}{M}{\left(\frac{2M}{3(M+1)}\right)}^{\text{2}}{\text{sin}}^{\text{2}}\theta -1\end{array}\right\}} \end{gathered}$$

Haciendo algunas operaciones llegamos al resultado

${\displaystyle Q=-\frac{1-e^2+\left(e^2-\frac{2}{3}\right){\text{sin}}^2{\theta }_1}{M+1}\frac{1}{2}{m}_1{u}_1^2}$

Caso particular: choques frontales

Cuando el parámetro de impacto b=0, o θ₁=0, el choque se denomina frontal

• Los ángulos que forman las velocidades con la recta que une los centros de los discos son φ₁=0 y φ₂ =0.
• Las velocidades angulares de rotación de los discos son ω₁=0 y ω₂ =0
• Las velocidades v₁ y v₂ de los centros de los discos después del choque son:

${\displaystyle v_1=\frac{(M-e)}{M+1}{u}_1{v}_2=\frac{M(1+e)}{M+1}{u}_1}$

que son las ecuaciones que se han obtenido para los choques frontales cuando la segunda partícula está en reposo u₂=0 antes del choque y se define M=m₁/m₂.

La energía perdida en el choque es

${\displaystyle Q=-\frac{\left(1-e^2\right)}{M+1}\frac{1}{2}{m}_1{u}_1^2}$

es decir, la fracción (1-e²)/(M+1) de la energía cinética de del disco incidente.

Ángulo crítico

Comparemos los valores de los ángulos de los discos después del choque φ₁ y φ₂ en los dos casos estudiados

• Hay deslizamiento

tanφ₂ =μ

${\displaystyle \tan {\phi }_1=\frac{M+1}{M-e}\tan {\theta }_1-\frac{\mu (1+e)}{M-e}}$

• No hay deslizamiento

${\displaystyle \tan {\phi }_1=\frac{\text{3}M+\text{2}}{3(M-e)}\tan {\theta }_1\tan {\phi }_2=\frac{\text{1}}{3(1+e)}\tan {\theta }_1}$

• Comprobamos que para el ángulo crítico θ_c

tanθ_c=3(1+e)μ

Las expresiones de los ángulos φ₁ y φ₂ coinciden

${\displaystyle \tan {\phi }_1=\frac{\text{3}M+\text{2}}{(M-e)}(1+e)}$

tanφ₂ =μ

• Si θ₁<θ_c utilizamos las fórmulas deducidas en el apartado no hay deslizamiento

• Si θ₁>θ_c utilizamos las fórmulas deducidas en el apartado hay deslizamiento

Medida de los ángulos en el laboratorio

En el laboratorio se mide el parámetro de impacto b, que está relacionado con el ángulo θ₁, que forma la dirección del la velocidad $\overrightarrow{u_1}$ del disco incidente con la línea que une los centros de los dos discos.

b=(r₁+r₂)·sinθ₁

y los ángulos ø₁ y ø₂ que forman las velocidades $\overrightarrow{v_1}$ y $\overrightarrow{v_2}$ de los discos después del choque con la dirección de la velocidad del primer disco $\overrightarrow{u_1}$. Estos ángulos, como puede fácilmente deducirse de la figura son

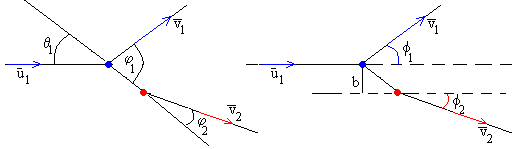
ø₁=φ₁-θ₁
ø₂=θ₁-φ₂

Ejemplos

Ejemplo 1:

Datos relativos a los discos

• Cociente M=m₁/m₂=1 entre las masa de los discos,
• Radios de los discos r₂=1 y r₁=1
• Discos ambos de acero, e=0.94 y μ =0.10

Antes del choque

• Velocidad inicial u₁=3.5 del primer disco
• Parámetro de impacto b=1.5.

Dado el parámetro de impacto calculamos el ángulo θ₁

1.5=(1+1)·sinθ₁               θ₁ =48.6º

El ángulo crítico es

tanθ_c=3(1+0.94)0.1          θ_c=30.2º

Estamos en el caso hay deslizamiento

Después del choque

• Módulo de la velocidad de la primer disco v₁ después del choque y su dirección φ₁

${\displaystyle \begin{array}{l}{v}_1\text{sin}{\phi }_1=\left(\text{sin48}\text{.6}-\frac{0.1(1+0.94)}{1+1}\cos 48.6\right)3.5=2.400\\ v_1\text{cos}{\phi }_1=\frac{1-0.94}{1+1}3.5\cos 48.6=0.069\end{array}}$

v₁=2.40, φ₁=88.3º

Ángulo medido en el laboratorio ø₁=88.3-48.6=39.7º (por encima de la horizontal)

• Módulo de la velocidad de la segundo disco v₂ después del choque y su dirección φ₂

tanφ₂ =0.1                 φ₂ =5.7º

${\displaystyle v_2=\frac{1(1+0.94)}{(1+1)}\sqrt{1+{0.1}^2}3.5\cos 48.6v_2=2.26}$

Ángulo medido en el laboratorio ø₂=48.6-5.7=42.9º (por debajo de la horizontal)

• Velocidades angulares de rotación de los discos ω₁ y ω₂

${\displaystyle \begin{array}{l}{r}_1{\omega }_1=\frac{2·0.1(1+0.94)}{1+1}3.5\cos 48.6r_1{\omega }_1=0.45\\ r_2{\omega }_2=0.45\end{array}}$

(Las velocidades angulares son positivas en el sentido de las agujas del reloj)

• Energía perdida en la colisión

${\displaystyle Q=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2+\frac{1}{2}\left(\frac{1}{2}{m}_1{r}_1^2\right){\omega }_1^2+\frac{1}{2}\left(\frac{1}{2}{m}_2{r}_2^2\right){\omega }_2^2-\frac{1}{2}{m}_1{u}_1^2}$

Q=-0.594

Mediante la fórmula

$$\begin{gathered} {\displaystyle Q=-\frac{0.1(1+0.94)\text{sin}(2·48.6)+\left(1-{0.94}^2-3·{0.1}^2{(1+0.94)}^2\right){\cos }^{2}48.6}{1+1} \\ \frac{1}{2}1·{3.5}^2=-0.594} \end{gathered}$$

Ejemplo 2º.

Datos relativos a los discos

• Masas de los discos m₁=0.5, m₂=1
• Radios de los discos r₁=2, r₂=1
• Discos ambos de acero, e=0.94 y μ =0.10

Antes del choque

• Velocidad inicial u₁=3.5 del primer disco
• Parámetro de impacto b=0.4.

0.4=(2+1)·sinθ₁               θ₁ =7.7º

El ángulo crítico es

tanθ_c=3(1+0.94)0.1          θ_c=30.2º

Estamos en el caso no hay deslizamiento

Después del choque

• Módulo de la velocidad de la segundo disco v₂ después del choque y su dirección φ₂

${\displaystyle \begin{array}{l}{v}_2\text{sin}{\phi }_2=\frac{0.5}{3(0.5+1)}\text{3}\text{.5·sin7}\text{.7}=0.052\\ v_2\text{cos}{\phi }_2=\frac{(1+0.94)0.5}{0.5+1}\text{3}\text{.5·cos7}\text{.7}=\text{2}\text{.243}\end{array}}$

v₂=2.244         φ₂ =1.3

Ángulo medido en el laboratorio ø₂=7.7-1.3=6.4º (por debajo de la horizontal)

• Módulo de la velocidad de la primer disco v₁ después del choque y su dirección φ₁

${\displaystyle \begin{array}{l}{v}_1\text{sin}{\phi }_1=\frac{3·0.5+2}{3(0.5+1)}\text{3}\text{.5·sin7}\text{.7}=\text{0}\text{.363}\\ v_1\text{cos}{\phi }_1=\frac{0.5-0.94}{(0.5+1)}\text{3}\text{.5·cos7}\text{.7}=\text{-1}\text{.017}\end{array}}$

v₁=1.080         φ₁ =160.4º

Ángulo medido en el laboratorio ø₁=160.4-7.7=152.7º (por encima de la horizontal)

• Velocidades angulares de rotación de los discos ω₁ y ω₂

${\displaystyle \begin{array}{l}{r}_1{\omega }_1=\frac{2}{3(0.5+1)}\text{3}\text{.5·sin7}\text{.7}=\text{0}\text{.207}\\ r_2{\omega }_2=\frac{2·0.5}{3(0.5+1)}\text{3}\text{.5·sin7}\text{.7}=\text{0}\text{.104}\end{array}}$

(Las velocidades angulares son positivas en el sentido de las agujas del reloj)

• Energía perdida en la colisión

${\displaystyle Q=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2+\frac{1}{2}\left(\frac{1}{2}{m}_1{r}_1^2\right){\omega }_1^2+\frac{1}{2}\left(\frac{1}{2}{m}_2{r}_2^2\right){\omega }_2^2-\frac{1}{2}{m}_1{u}_1^2}$

Q=-0.246

Mediante la fórmula

${\displaystyle Q=-\frac{1-{0.94}^2+\left({0.94}^2-\frac{2}{3}\right){\text{sin}}^{2}7.7}{0.5+1}\frac{1}{2}0.5·{3.5}^2=-0.246}$

Actividades

En la tabla tenemos los datos correspondientes al coeficiente de rozamiento μ y al coeficiente de restitución e.

Fuente: Doménech A, Doménech M.T. Colisiones inelásticas de esferas. Revista Española de Física 4, 3 (1990) págs. 52-56.

Se introduce

• La masa m₁ del primer disco, en el control titulado Masa m₁
• El radio r₁ del primer disco, en el control titulado Radio r₁
• Materiales de los que están hechos los discos, en el control titulado Materiales de los discos
• Velocidad inicial u₁ del primer disco, en el control titulado Velocidad inicial
• El segundo disco está inicialmente en reposo u₂=0 en el origen su masa m₂=1 y su radio r₂=1
• Parámetro de impacto, b, un número comprendido entre 0 y (r₁+r₂),en el control titulado P. impacto. El valor 0 es para los choques frontales.
• La velocidad angular inicial de los discos es nula ω₁=ω₂=0

Se pulsa el botón titulado Nuevo.

Observamos el movimiento de los discos antes y después del choque en el Sistema de Referencia del Laboratorio

El programa interactivo calcula:

• Las velocidades lineales v₁ y v₂ de los discos después del choque
• Los ángulos de desviación ø₁ y ø₂ de los discos respecto de la dirección del disco incidente.
• Las velocidades angulares ω₁ y ω₂ de los discos después del choque
• La energía Q perdida en la colisión

Con los datos introducidos y calculados por el programa, verificaremos los principios de conservación del momento lineal y angular tal como se ha efectuado en los ejemplos.

Referencias

Doménech A, Doménech M.T. Analysis of two-disc collisions. Eur. J. Phys. 14 (1993) pp. 177-183.