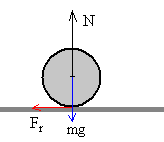
Las fuerzas que actúan sobre la pelota son: el peso mg, la fuerza normal o reacción del suelo N, y la fuerza de rozamiento F_r=μN. Durante el choque el peso mg es despreciable frente a la fuerza normal N.

Consideremos una pelota de tenis que se deja caer desde un metro de altura, que tiene un coeficiente de restitución de e=0.78 y que el tiempo de contacto de la pelota con el suelo es de Δt=0.005 s. La velocidad de la pelota antes del choque es u_y y la velocidad de la pelota después del choque es v_y=–e·u_y. La aceleración es

${\displaystyle a_y=\frac{u_y-(-e{u}_y)}{\Delta t}=\frac{\sqrt{2gh}(1+e)}{\Delta t}=1600{\text{m/s}}^{\text{2}}}$

mucho mayor que la aceleración de la gravedad g=9.8 m/s² . Como

ma_y=N-mg

Por tanto, el peso mg se puede despreciar frente a la fuerza normal N.

En general, es bastante complicado el análisis del choque de una pelota con el suelo, ya que la pelota modifica en mayor o menor grado su forma esférica durante el choque. Por otra parte, una pelota no es un cuerpo homogéneo, sino una capa esférica delgada hecha de goma en cuyo interior hay aire a presión. Para evitar estas complicaciones, en esta página vamos a estudiar el choque de un disco indeformable con una pared rígida.

Modelo simple de choque de un disco con una pared rígida

Definimos el coeficiente de restitución e como

${\displaystyle e=-\frac{v_1-v_2}{u_1-u_2}}$

donde v₁ y v₂ son las velocidades del las partículas después del choque y u₁ y u₂ las velocidades antes del choque.

La partícula 2 es ahora la pared cuya velocidad antes y después del choque es cero u₂=v₂=0

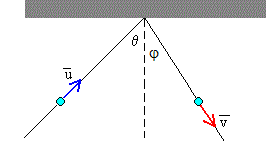
El disco se acerca hacia la pared con una velocidad u₁=u·cosθ y se aleja de la pared con una velocidad v₁=-v·cosφ .

La relación entre velocidades será

u·sinθ =v·sinφ
u·e·cosθ =v·cosφ .

La relación entre los ángulos de incidencia θ y reflexión φ  es 

tanθ =e·tanφ

Conocido el coeficiente de restitución e y el ángulo de incidencia θ, calculamos el ángulo de reflexión φ. Conocida la velocidad de la partícula incidente u, obtenemos la velocidad de la partícula reflejada v.

Choque de un disco con una pared rígida

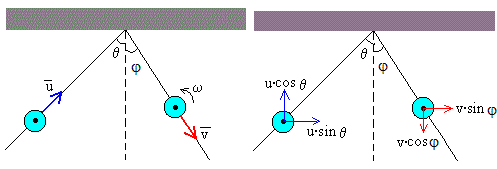
1. De la definición de coeficiente de restitución tenemos

e·u·cosθ =v·cosφ  (1)

2. Momento angular respecto de P, punto de contacto con la pared rígida.



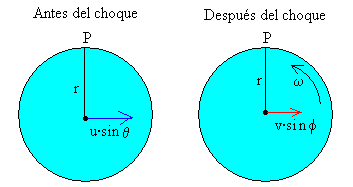
Como las fuerzas que ejerce la pared sobre el disco actúan en P. El momento de dichas fuerzas respecto de P es cero. El momento angular respecto de dicho punto será constante.

${\displaystyle \overrightarrow{M_{ext}}=\frac{d\overrightarrow{L}}{dt}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

La constancia del momento angular para un disco de momento de inercia I=mr²/2, que gira con velocidad angular ω en el sentido indicado después del choque, se escribe

r·mv·sinφ +I·ω =r·mu·sinθ   

rω=2u·sinθ  -2v·sinφ   (2)

Tenemos dos ecuaciones y tres incógnitas

• La velocidad del centro del disco después del choque v y su dirección φ
• La velocidad angular de rotación del disco, ω

Precisamos una ecuación más para resolver el problema.

Fuerzas sobre el disco

El disco permanece en contacto con la pared un tiempo pequeño Δt. Las fuerzas sobre el disco son:

• La reacción N de la pared rígida
• La fuerza de rozamiento que se opone a la velocidad del punto P de contacto de la bola con el suelo.

v_P=v_x-ω r

Inicialmente la velocidad de traslación del c.m. es v_x=u·sinθ y la velocidad angular de rotación es ω=0. La fuerza de rozamiento disminuirá la velocidad de traslación del c.m. e incrementará la velocidad de rotación. Al final del intervalo de tiempo Δt pueden ocurrir dos casos:

1. El disco no desliza

La velocidad del punto P de contacto entre el disco y la pared es cero.

v_P=v·sinφ-ωr=0   (3)

Resolviendo un sistema de tres ecuaciones con tres incógnitas

Estas tres ecuaciones nos permiten determinar la velocidad del disco después del choque v, su velocidad angular de rotación ω y el ángulo φ que forma con la dirección normal a la pared, con los datos de la velocidad inicial u y del ángulo de incidencia θ .

Despejamos rω de la ecuación (3) y sustituimos en la ecuación (2)

v·sinφ  =(2/3)·u·sinθ
v·cosφ  =e·u·cosθ

${\displaystyle \tan \phi =\frac{2\tan \theta }{3e}}$

La velocidad angular de rotación ωr se despeja en las ecuación (3)

ω r=(2/3)u·sinθ .

Balance energético

La energía cinética inicial del disco es

${\displaystyle E_i=\frac{1}{2}m{u}^2}$

La energía cinética final del disco es

${\displaystyle E_f=\frac{1}{2}m{v}^2+\frac{1}{2}I{\omega }^2=\frac{1}{2}m{v}^2+\frac{1}{4}m{\left(\omega r\right)}^2}$

La energía Q perdida en la colisión es

${\displaystyle Q=E_f-E_i=\frac{1}{2}m{u}^2\left(e^2-1+\left(\frac{2}{3}-e^2\right){\text{sin}}^2\theta \right)}$

2. El disco desliza



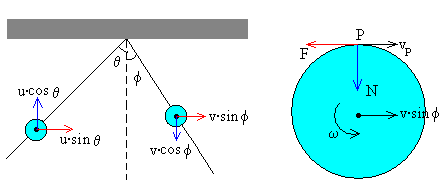
La pared ejerce sobre el disco dos fuerzas, la reacción N y la fuerza F que se opone a que el disco deslice sobre la pared y que es de sentido contrario a v_P>0, la velocidad del punto de contacto entre el disco y la pared. La fuerza de rozamiento F disminuirá la velocidad de traslación del c.m. y aumentará la velocidad angular de rotación. En este caso, el intervalo de tiempo Δt que dura el choque no es suficiente para que se establezca el equilibrio entre traslación y rotación v_P=0.

La fuerza N actuando durante el pequeño intervalo de tiempo Δt que el disco está en contacto con la pared modifica la componente normal del momento lineal del disco. De modo análogo, el impulso de la fuerza F modifica la componente paralela al plano del momento lineal del disco.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\Delta t}{\int }}N·dt}=mv\cos \phi -(-mu\cos \theta )\\ -{\displaystyle \underset{0}{\overset{\Delta t}{\int }}F·dt}=mv\text{sin}\phi -mu\text{sin}\theta \end{array}}$

Teniendo en cuenta la relación entre ambas fuerzas, F=μ·N, obtenemos la ecuación que sustituye a (3)

-mv·sinφ +mu·sinθ =μ (mv·cosφ +mu·cosθ )   (3)

Resolviendo un sistema de tres ecuaciones con tres incógnitas

Sustituimos v·cosφ de la ecuación (1) en la (3)

v·sinφ =u·sinθ -μ u(1+e)·cosθ
v·cosφ =e·u·cosθ

Dividiendo miembro a miembro por la ecuación (1), nos permite establecer la relación entre el ángulo de incidencia θ , y el reflejado φ

${\displaystyle \tan \phi =\frac{1}{e}\left(\tan \theta -\mu (1+e)\right)}$

Una vez calculado el ángulo φ,  despejamos la velocidad angular del disco rω de la ecuación (2)

rω=2u·sinθ  -2v·sinφ =2μ (1+e)·u·cosθ

Balance energético

La energía perdida en la colisión Q vale

$$\begin{gathered} {\displaystyle Q=\frac{1}{2}m{v}^2+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\omega }^2-\frac{1}{2}m{u}^2= \\ \frac{1}{2}m{u}^2\left(\left(e^2+3{\mu }^2{(1+e)}^2-1\right){\cos }^2\theta -\mu (1+e)\text{sin}2\theta \right)} \end{gathered}$$

Ángulo crítico

Cuando el disco no desliza v_P=0, la relación entre la fuerza F y la reacción N es desconocida. La relación entre el ángulo reflejado y el incidente como hemos visto es

${\displaystyle \tan \phi =\frac{2}{3e}\tan \theta }$

Cuando el disco desliza v_P≠ 0, la relación entre ambas fuerzas es F=μ·N,

${\displaystyle \tan \phi =\frac{1}{e}\left(\tan \theta -\mu (1+e)\right)}$

El ángulo crítico incidente θ_c será aquél en la que el disco comienza a deslizar cumpliéndose ambas condiciones a la vez (supondremos que el coeficiente de rozamiento estático y dinámico son iguales). Por tanto,

tanθ_c=3μ (1+e)

• Si θ<θ_c utilizamos las fórmulas deducidas en el apartado el disco no desliza

• Si θ>θ_c utilizamos las fórmulas deducidas en el apartado disco desliza

Caso particular: Choque elásticos

Cuando μ =0 y e=1,

El ángulo crítico θ_L=0. Para cualquier ángulo incidente θ estamos en el caso el disco desliza

• Se cumple que el ángulo incidente es igual al reflejado φ=θ
• El disco no gira después del choque rω=0
• La energía perdida en el choque Q=0

Ejemplos

En la tabla tenemos los datos correspondientes al coeficiente de rozamiento μ y al coeficiente de restitución e.

Fuente: Doménech A, Doménech M.T. Colisiones inelásticas de esferas. Revista Española de Física 4, 3 (1990) págs. 52-56.

Elegimos, acero-acero

• μ =0.1
• e=0.94

El ángulo crítico es

tanθ_c=3μ (1+e)       θ_c=8.8º

• Ángulo incidente, θ=45º

• Velocidad del disco antes del choque, u=3.5

El ángulo θ >θ_c el disco desliza

1. El ángulo después del choque se obtiene con la fórmula

${\displaystyle \tan \phi =\frac{1}{e}\left(\tan \theta -\mu (1+e)\right)}$

El valor de φ=40.61º

2. Calculamos la velocidad v después del choque mediante

v·cosφ =e·u·cosθ

Se despeja v=3.06

3. La velocidad angular de rotación ω (o mejor rω ), se obtiene mediante la relación

rω =2μ (1+e)·u·cosθ

Se obtiene rω=0.96

La velocidad del punto P de contacto entre el disco y la pared es v_P=v·sinφ -rω>0, por tanto, el disco desliza.

4. La energía perdida en el choque es la diferencia entre la energía final (de traslación y de rotación) y la inicial (de traslación).

Q=-1.2m

El ángulo θ <θ_c el disco no desliza.

• Ángulo incidente, θ=5º

1. El ángulo después del choque se obtiene con la fórmula

${\displaystyle \tan \phi =\frac{2}{3e}\tan \theta }$

El valor de φ=3.55º

2. Calculamos la velocidad después del choque mediante el coeficiente de restitución

v·cosφ =e·u·cosθ

Se despeja v=3.28

3. La velocidad angular de rotación ω (o mejor rω ), se obtiene mediante la relación

rω =(2u/3)·sinθ

rω =0.203

La velocidad del punto P de contacto entre el disco y la pared es v_P=v·sinφ-rω=0, por tanto, el disco no desliza.

4. La energía perdida en la colisión es

Q=-072·m

Actividades

Se introduce

• Los materiales de los que está hechos el disco que choca con la pared, en el control Materiales
• El ángulo incidente, en el control titulado Ángulo.
• La velocidad del disco antes del choque, en el control titulado Velocidad inicial.

Se pulsa el botón titulado Nuevo

El programa interactivo calcula la velocidad del disco después del choque v, su velocidad angular de rotación ω y el ángulo φ que forma con la dirección normal a la pared, con los datos de la velocidad inicial u y del ángulo incidente θ .

Referencias

Doménech A, Doménech M.T. Analysis of two-disc collisions. Eur. J. Phys. 14 (1993), pp. 177-183.