Movimiento en el cono

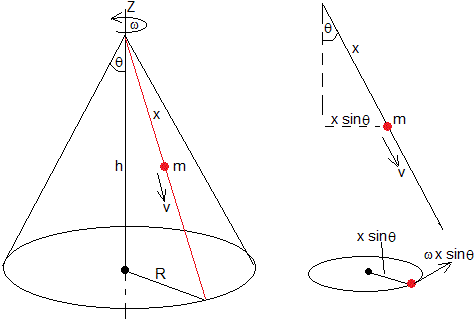
Sea un cono de altura h y radio de la base R. Supongamos que se ha hecho una ranura a lo largo del cono, desde el vértice a la base, señalada por la línea de color rojo en la figura.

El cono gira alrededor del eje Z con velocidad angular ω₀. Una partícula de masa m se suelta en el vértice deslizando por la ranura sin rozamiento alguno, tal como se indica en la figura. Vamos a estudiar el movimiento de la partícula y del cono y calcularemos la velocidad angular del cono cuando la partícula llege a su base

El momento de inercia del cono macizo alrededor del eje Z es I₀=3MR²/10. Siendo M la masa del cono

En el instante t=0, la partícula de masa m se encuentra en el vértice del cono que gira con velocidad angular ω₀. El momento angular es I₀ω₀ y la energía inicial del sistema es

${\displaystyle E=\frac{1}{2}{I}_0{\omega }_0^2}$

En el instante t, la velocidad angular de rotación alrededor del eje Z del cono es ω. La partícula se ha desplazado x a lo largo de la ranura, su distancia al eje de rotación es xsinθ. Su velocidad tiene dos componentes: una v paralela a la ranura, y otra ωxsinθ correspondiente a la rotación alrededor del eje Z con velocidad angular ω.

Se conserva el momento angular del sistema formado por el cono y la partícula

${\displaystyle I_0{\omega }_0=\left(I_0+m{x}^2{\sin }^2\theta \right)\omega }$

Se conserva la energía (suma de la energía cinética de la partícula, de rotación del cono y la energía potencial correspondiente a una altura xcosθ)

${\displaystyle \frac{1}{2}{I}_0{\omega }_0^2=\frac{1}{2}m\left(v^2+{\omega }^2{x}^2{\sin }^2\theta \right)+\frac{1}{2}{I}_0{\omega }^2-mgx\cos \theta }$

Cuando la partícula llega a la base del cono, xsinθ=R, xcosθ=h, la velocidad angular ω del cono es

${\displaystyle \omega =\frac{I_0{\omega }_0}{I_0+m{R}^2}}$

La velocidad final v de la partícula a lo largo de la ranura es

${\displaystyle v^2=\frac{I_0{\omega }_0^2{R}^2}{I_0+m{R}^2}+2gh}$

Ecuación del movimiento

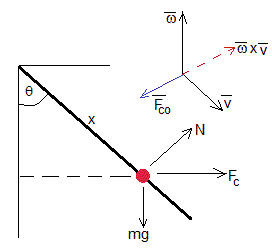
En el sistema de referencia no inercial en rotación del cono. Las fuerzas que actúan sobre la partícula son:

• El peso, mg
• La reacción de la ranura, N
• La fuerza centrífuga, $\overrightarrow{F_c}=-m\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)$, cuyo módulo es mω²xsinθ.
• La fuerza de Coriolis, $\overrightarrow{F_{co}}=-2m\overrightarrow{\omega }\times \overrightarrow{v}$, es perpendicular al plano del dibujo y dirigida hacia el lector. No contribuye al movimiento de la partícula. Se anula con la fuerza de reacción de sentido contrario, proporcionada por la ranura

La ecuación del movimiento a lo largo de la ranura es

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=mg\cos \theta +\left(m{\omega }^{2}x\sin \theta \right)\sin \theta \\ \frac{d^{2}x}{d{t}^2}=g\cos \theta +{\left(\frac{I_0{\omega }_0}{I_0+m{x}^2{\sin }^2\theta }\right)}^{2}x{\sin }^2\theta \end{array}}$

El ángulo girado por el cono φ en función del tiempo es

${\displaystyle \frac{d\phi }{dt}=\frac{I_0{\omega }_0}{I_0+m{x}^2{\sin }^2\theta }}$

Tenemos que resolver un sistema de dos ecuaciones diferenciales, con las siguientes condiciones iniciales: en el instante t=0, x=0 y dx/dt=0, la partícula parte del vértice del cono en reposo. El ángulo inicial girado por el cono, φ=0

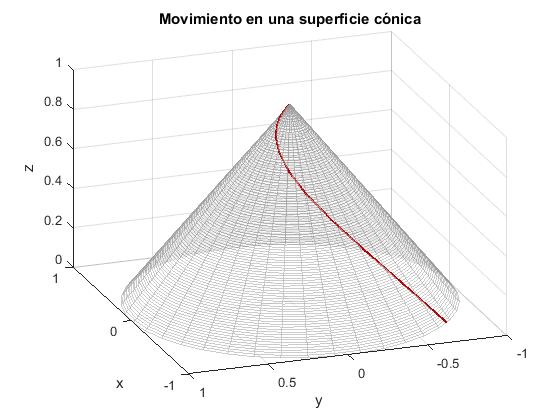
Considermos un cono de masa M=1, altura h=1 y ángulo θ=45°. El cono gira inicialmente con velocidad angular ω₀=10 rad/s, cuando la partícula de masa m=0.5 kg se encuentra en el vértice del cono. La partícula empieza a deslizar sin rozamiento por la ranura. Representamos el cono y la trayectoria de la partícula sobre su suerficie, resolviendo el sistema de dos ecuaciones diferenciales mediante la función ode45 de MATLAB

theta=pi/4; %ángulo del cono
h=1;  %altura del cono
I0=3*h^2*tan(theta)^2/10; %momento de inercia del cono, M=1
m=0.5; %masa partícula
w0=10; %velocidad angular inicial de rotación

opts=odeset('events',@(t,x) cono_gira_ode45(t,x,h,theta));
fg=@(t,x)[x(2); 9.8*cos(theta)+x(1)*sin(theta)^2*
(I0*w0/(I0+m*x(1)^2*sin(theta)^2))^2; I0*w0/(I0+m*x(1)^2*sin(theta)^2)];
[t,x]=ode45(fg,[0,10],[0,0,0], opts);
xp=x(:,1).*cos(x(:,3))*sin(theta);
yp=x(:,1).*sin(x(:,3))*sin(theta);
zp=h-x(:,1)*cos(theta);
fprintf('tiempo: %1.2f, velocidad angular: %1.2f, velocidad partícula: 
%1.2f\n',t(end),I0*w0/(I0+m*x(end,1)^2*sin(theta)^2),x(end,2))

hold on
view(250,30)
%superficie cónica
phi=linspace(0,2*pi,40);
r=linspace(0,h/cos(theta));
[phi,r]=meshgrid(phi,r);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=h-r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6], 'FaceAlpha',0.5,'EdgeAlpha',0.5)

%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
 
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en una superficie cónica')

Cuando la partícula llega a la base del cono

tiempo: 0.47, velocidad angular: 3.75, velocidad partícula: 7.56

Definimos una función para que interrumpa el proceso de integración cuando la partícula llegue a la base del cono x=h/cosθ

function [detect,stopin,direction]=cono_gira_ode45(~,x, h, theta)
    detect=x(1)-h/cos(theta); 
    stopin=1;
    direction=1; 
end

Actividades

Se introduce

• El ángulo θ del cono, en el control titulado Angulo
• La masa m de la partícula, en el control titulado Masa
• La masa del cono se ha fijado en M=1 kg
• la altura del cono se ha fijado en h=1 m
• La velocidad angular inicial de rotación se ha fijado en ω₀=10 rad/s

Observamos el movimiento de la partícula sobre la superficie del cono

En la parte izquierda se proporcionan los datos de

• El tiempo t
• El desplazamiento x de la partícula a lo largo de la ranura en la superficie del cono
• La velocidad v de la partícula en su movimiento a lo largo de la ranura
• La velocidad angular ω de rotación del cono
• La energía del sistema que deberá permanecer constante e igual a la energía inicial

Movimiento en la esfera

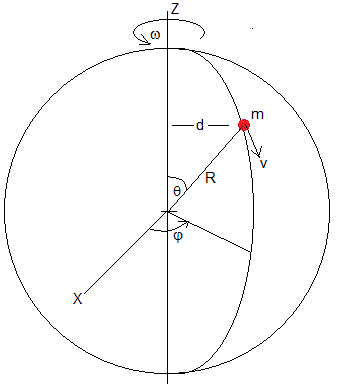
Una esfera de masa M y radio R gira alrededor de un eje fijo Z con velocidad angular ω₀. Una partícula de masa m se desplaza con velocidad v constante a lo largo de un meridiano.

En el instante inicial t=0, la partícula se encuentra en el polo norte θ=0, cuando la velocidad angular de rotación de la esfera es ω₀.

Vamos a calcular el ángulo de girado por la esfera φ, cuando la partícula llega al polo Sur, θ=π

Aplicamos el principio de conservación del momento angular

${\displaystyle \left(\frac{2}{5}M{R}^2\right){\omega }_0=\left(\frac{2}{5}M{R}^2+m{d}^2\right)\omega }$

La distancia de la partícula al eje de rotación es d=Rsinθ. La velocidad angular de rotación ω=dφ/dt. En el instante t la partícula se encuentra sobre el meridiano en la posición Rθ=v·t.

${\displaystyle \omega =\frac{2}{2+5\frac{m}{M}{\sin }^2\theta }{\omega }_0}$

Representamos la velocidad angular de rotación ω para m/M=1/2 y ω₀=1

w0=1; %velocidad angular inicial de rotación
m_M=1/2; %relación entre masas
w=@(x) 2*w0./(2+5*m_M*sin(x).^2);
fplot(w,[0,pi])
grid on
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
xlabel('\theta')
ylabel('\omega')
title('Velocidad angular de rotación')

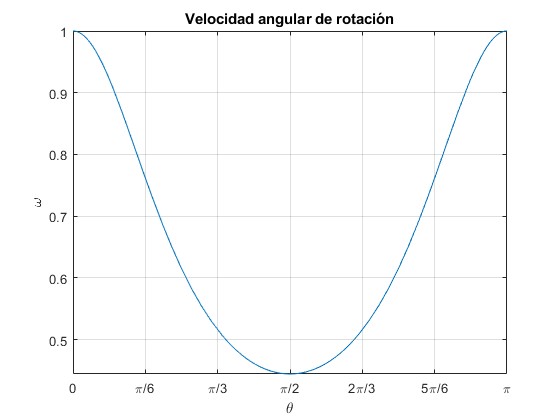
El momento de inercia es máximo en el ecuador θ=π/2 y mínimo en los polos, θ=0, π. La velocidad angular de rotación ω le ocurre la inversa, es máxima en los polos y mínima en el ecuador

La conservación del momento angular se escribe

${\displaystyle \frac{2}{5}M{\omega }_0=\left(\frac{2}{5}M+m{\sin }^2\left(\frac{vt}{R}\right)\right)\frac{d\phi }{dt}}$

La partícula llega al polo sur θ=π en el instante T=πR/v. El ángulo girado φ por la esfera es

${\displaystyle \phi ={\displaystyle \underset{0}{\overset{T}{\int }}\frac{2{\omega }_0}{2+5\frac{m}{M}{\sin }^2\left(\frac{vt}{R}\right)}dt}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}x=\frac{2vt}{R},dx=\frac{2v}{R}dt\\ \phi =\frac{R{\omega }_0}{v}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{dx}{2+5\frac{m}{M}{\sin }^2\left(\frac{x}{2}\right)}}\end{array}}$

Empleamos la relación trigonométrica

${\displaystyle \begin{array}{l}\cos x={\cos }^2\left(\frac{x}{2}\right)-{\sin }^2\left(\frac{x}{2}\right)=1-2{\sin }^2\left(\frac{x}{2}\right)\\ \phi =\frac{R{\omega }_0}{v}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{dx}{2+5\frac{m}{M}\left(\frac{1-\cos x}{2}\right)}}=\frac{R{\omega }_0}{v}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{dx}{\left(2+\frac{5}{2}\frac{m}{M}\right)-\frac{5}{2}\frac{m}{M}\cos x}}\end{array}}$

Efectuamos un nuevo cambio de variable para calcular la integral

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dx}{a-b\cos x}}\\ \tan \left(\frac{x}{2}\right)=t,\frac{1}{2}\frac{dx}{{\cos }^2\left(\frac{x}{2}\right)}=dt,\left(1+{\tan }^2\left(\frac{x}{2}\right)\right)dx=dt,dx=\frac{2dt}{1+t^2}\\ \cos x={\cos }^2\left(\frac{x}{2}\right)-{\sin }^2\left(\frac{x}{2}\right)=\frac{1}{1+t^2}-\frac{t^2}{1+t^2}=\frac{1-t^2}{1+t^2}\\ {\displaystyle \int \frac{\frac{2dt}{1+t^2}}{a-b\frac{1-t^2}{1+t^2}}}={\displaystyle \int \frac{2dt}{a\left(1+t^2\right)-b\left(1-t^2\right)}}={\displaystyle \int \frac{2dt}{\left(a+b\right)t^2+\left(a-b\right)}}=\frac{2}{a+b}{\displaystyle \int \frac{dt}{t^2+\frac{a-b}{a+b}},a>b}\\ =\frac{2}{a+b}\frac{1}{\sqrt{\frac{a-b}{a+b}}}\arctan \left(\frac{t}{\sqrt{\frac{a-b}{a+b}}}\right)=\frac{2}{\sqrt{a^2-b^2}}\arctan \left(t\sqrt{\frac{a+b}{a-b}}\right)=\frac{2}{\sqrt{a^2-b^2}}\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan \left(\frac{x}{2}\right)\right)\end{array}}$

La integral definida es

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{dx}{a-b\cos x}=}\frac{2}{\sqrt{a^2-b^2}}\left\{\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan \pi \right)-\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan 0\right)\right\}=\frac{2\pi }{\sqrt{a^2-b^2}}}$

No parece muy claro que el resultado entre las llaves sea π, por lo que representamos el integrando para m/M=1/2, es decir, para a=13/4 y b=5/4. Comparamos el resultado obtenido con la integración por el procedimiento numérico integral de MATLAB

%m/M=1/2; %relación entre masas
a=13/4;
b=5/4;
f=@(x) 1./(a-b*cos(x));
fplot(f,[0,2*pi])
grid on
set(gca,'XTick',0:pi/4:2*pi)
set(gca,'XTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi',
'5\pi/4','3\pi/2','7\pi/4','2\pi'})
xlabel('\theta')
ylabel('f(\theta)')
title('Integral')

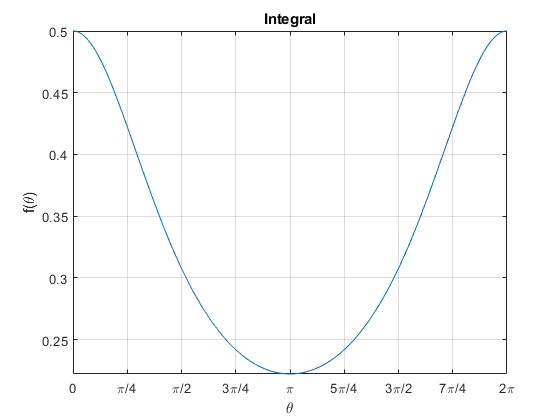
>> integral(f,0,2*pi)
ans =    2.0944
>> 2*pi/sqrt(a^2-b^2)
ans =   2.0944

Los resultados coinciden

Finalmente, el ángulo girado φ por la esfera alrededor del eje Z, cuando la partícula se mueve a lo largo de un meridiano partiendo del polo norte y llegando al sur

${\displaystyle \begin{array}{l}\phi =\frac{R{\omega }_0}{v}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{dx}{\left(2+\frac{5}{2}\frac{m}{M}\right)-\frac{5}{2}\frac{m}{M}\cos x}}=\frac{R{\omega }_0}{v}\frac{2\pi }{\sqrt{{\left(2+\frac{5}{2}\frac{m}{M}\right)}^2-{\left(\frac{5}{2}\frac{m}{M}\right)}^2}}\\ \phi =\frac{R{\omega }_0}{v}\frac{2\pi }{\sqrt{4+10\frac{m}{M}}}=\frac{\pi R{\omega }_0}{v}\sqrt{\frac{2M}{2M+5m}}\end{array}}$

Trayectoria de a partícula en el Sistema Inercial

La trayectoria de la partícula en el Sistema de Referencia en rotación es media circunferencia (un meridiano)

Vamos a representar la trayectoria vista por un observador inercial, fuera de la esfera. Partimos del resultado

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{a-b\cos x}=}\frac{2}{\sqrt{a^2-b^2}}\left\{\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan \left(\frac{x}{2}\right)\right)-\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan 0\right)\right\}\\ =\frac{2}{\sqrt{a^2-b^2}}\left\{\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan \left(\frac{x}{2}\right)\right)\right\},x=\frac{2vt}{R}\end{array}}$

El ángulo girado φ en el instante t es

${\displaystyle \phi (t)=\frac{R{\omega }_0}{v}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{a-b\cos x}=}\frac{R{\omega }_0}{v}\frac{2}{\sqrt{a^2-b^2}}\left\{\arctan \left(\sqrt{\frac{a+b}{a-b}}\tan \left(\frac{vt}{R}\right)\right)\right\}}$

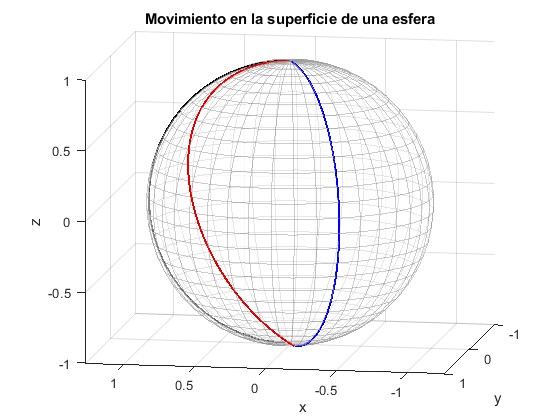
Representamos la trayectoria para

• radio de la esfera, R=1
• velocidad angular inicial de rotación, ω₀=1
• velocidad cosntante partícula, v=1
• cociente entre de la masa de la partícula y de la de la esfera, m/M=1/2

En color negro, la posición inicial del meridiano y en azul la final, el ángulo girado por la esfera es φ=2.0944·180/π=120°

%m/M=1/2; %relación entre masas
a=13/4;
b=5/4;
R=1; %radio esfera
w0=1; %velocidad angular inicial de rotación
v=1; %velocidad partícula
T=pi*R/v; %tiempo de viaje
tt=linspace(0,T,100);
phi=zeros(1,length(tt));
k=1;
f=@(x) 1./(a-b*cos(x));
for t=tt
    temp=atan(sqrt((a+b)/(a-b))*tan(v*t/R));
   if temp<0
       temp=pi+temp;
   end
    phi(k)=R*w0*2*temp/(v*sqrt(a^2-b^2));
     temp1=(R*w0/v)*integral(f,0,2*v*t/R);
     disp([phi(k), temp1])
     k=k+1;
end
th=v*tt/R;
xp=R*sin(th).*cos(phi);
yp=R*sin(th).*sin(phi);
zp=R*cos(th);
desplaza=phi(end);

%esfera
theta=linspace(0,pi,30);
phi=linspace(0,2*pi,40);
[theta, phi]=meshgrid(theta,phi);
x=R*sin(theta).*cos(phi);
y=R*sin(theta).*sin(phi);
z=R*cos(theta);
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5)
%meridianos inicial y final
theta=linspace(0,pi,30);
x=R*sin(theta);
y=zeros(1, length(x));
z=R*cos(theta);
h1=line(x,y,z);
set(h1,'Color','k','LineWidth',1.5)
x=R*sin(theta).*cos(desplaza);
y=R*sin(theta).*sin(desplaza);
z=R*cos(theta);
h1=line(x,y,z);
set(h1,'Color','b','LineWidth',1.5)

%trayectoria
 h1=line(xp,yp,zp);
set(h1,'Color',[.9,0,0],'LineWidth',1.5)
axis equal
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en la superficie de una esfera')
view (-170,10)

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1174, pp. 283-284

Sidney B. Cahn, Boris E. Nadgorny. A guide to physics problems, part 1. Mechanics, Relativity, and Electrodynamics.. Kluwer Academic Publishers, 2004. Problem 1.40