Choque de una bala con una varilla sujeta por una cuerda

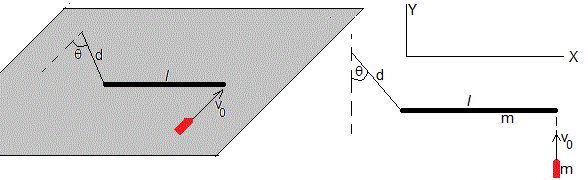
Sistema aislado, bala-varilla

Supongamos que la cuerda no existe, el sistema bala-varilla es aislado.

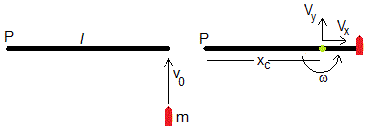
La velocidad de la bala es v₀, se incrusta en el extremo derecho de la varilla. Lo que hace que el centro de masas del conjunto se traslade con velocidad V y gire alrededor del centro de masas con velocidad angular ω

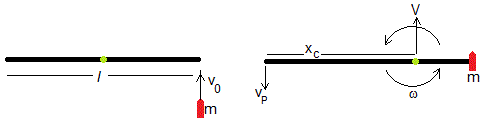
Conservación del momento lieal

$\begin{array}{l} m v_{0} = 2 m V \\ V = \frac{v_{0}}{2} \end{array}$

Conservación del momento angular

La posición del centro de masas del sistema bala-varilla es x_c

$x_{c} = \frac{m \frac{l}{2} + m l}{2 m} = \frac{3}{4} l$

El momento de inercia respecto a un eje perpendicular al plano horizontal y que pasa por el c. m. es

$I_{c m} = \frac{1}{12} m l^{2} + m {(x_{c} - \frac{l}{2})}^{2} + m {(l - x_{c})}^{2} = \frac{5}{24} m l^{2}$

La conservación del momento angular se expresa

$\begin{array}{l} m v_{0} (l - x_{c}) = I_{c m} ω \\ m v_{0} \frac{l}{4} = \frac{5}{24} m l^{2} ω \\ ω = \frac{6}{5} \frac{v_{0}}{l} \end{array}$

Velocidad del punto P situado en el extremo izquierdo de la varilla

La velocidad del punto P es la suma de la velocidad del centro de masas $\vec{V}$ y la velocidad del extremo del vector que une el centro de masas con el punto P, $\vec{r_{P}} - \vec{r_{c m}}$ cuya longitud es fija, su único movimiento es una rotación alrededor de une eje vertical con velocidad angular $\vec{ω}$

$\begin{array}{l} \vec{v_{P}} = \vec{V} + \vec{ω} \times (\vec{r_{P}} - \vec{r_{c m}}) \\ {\begin{cases} \vec{V} = \frac{v_{0}}{2} \hat{j} \\ \vec{ω} = \frac{6}{5} \frac{v_{0}}{l} \hat{k} \\ \vec{r_{P}} - \vec{r_{c m}} = - \frac{3}{4} l \hat{i} \end{cases} \\ \vec{v_{P}} = \frac{v_{0}}{2} \hat{j} - \frac{6}{5} \frac{v_{0}}{l} \frac{3}{4} l \hat{j} = - \frac{2}{5} v_{0} \hat{j} \end{array}$

Esto indica que el punto P gira en sentido contrario a las agujas del reloj, por lo que la cuerda permanecerá tensa inmediatamente después del choque. La tensión T de la cuerda ejercerá un impulso en el momento del choque.

Sistema no aislado bala-varilla

Consideramos el efecto de la cuerda tensa

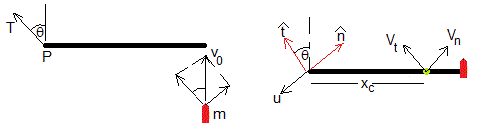
Sea $\hat{t}$ el vector unitario en la dirección de la cuerda tensa, y $\hat{n}$ el vector unitario en la dirección perpendicular. Descomponemos la velocidad $\vec{V}$ del centro de masas en ambas direcciones y también la velocidad $\vec{v_{0}}$ de la bala antes del choque

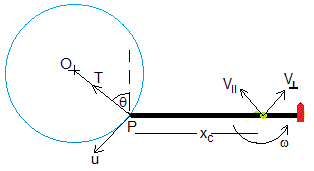
$\begin{array}{l} \hat{t} = - \sin θ \cdot \hat{i} + \cos θ \cdot \hat{j} \\ \hat{n} = \cos θ \cdot \hat{i} + \sin θ \cdot \hat{j} \\ \vec{V} = V_{t} \hat{t} + V_{n} \hat{n} \\ \vec{v_{0}} = v_{0} \cos θ \cdot \hat{t} + v_{0} \sin θ \cdot \hat{n} \end{array}$

Como la cuerda está tensa, el punto P describe un movimiento circular alrededor del punto fijo O, la sujeción del extremo de la cuerda tensa.

La velocidad u es perpendicular a la dirección radial, a la cuerda

Conservación del momento lineal

En la dirección $\hat{n}$ perpendicular a la tensión de la cuerda no hay fuerza externa, por lo que el momento lineal se conserva

$\begin{array}{l} m v_{0} \sin θ = 2 m V_{n} \\ V_{n} = \frac{1}{2} v_{0} \sin θ \end{array}$

Calculamos la velocidad u del punto P como en el apartado anterior

$\begin{array}{l} \vec{v_{P}} = \vec{V} + \vec{ω} \times (\vec{r_{P}} - \vec{r_{c m}}) \\ - u \hat{n} = V_{t} \hat{t} + V_{n} \hat{n} + | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 0 & ω \\ - x_{c} & 0 & 0 \end{matrix} | \\ - u \hat{n} = V_{t} \hat{t} + V_{n} \hat{n} - ω x_{c} \hat{j} \end{array}$

Multiplicando escalarmente por el vector $\hat{n}$

$\begin{array}{l} - u \hat{n} \cdot \hat{n} = V_{t} \hat{t} \cdot \hat{n} + V_{n} \hat{n} \hat{\cdot n} - ω x_{c} \hat{j} \cdot \hat{n} \\ - u = V_{n} - ω \frac{3 l}{4} \sin θ \\ V_{n} = \frac{3 l}{4} ω \sin θ - u \\ \frac{1}{2} v_{0} \sin θ = \frac{3 l}{4} ω \sin θ - u \end{array}$

Multiplicando escalarmente por el vector $\hat{t}$

$\begin{array}{l} - u \hat{n} \cdot \hat{t} = V_{∥} \hat{t} \cdot \hat{t} + V_{⊥} \hat{n} \hat{\cdot t} - ω x_{c} \hat{j} \cdot \hat{t} \\ 0 = V_{t} - ω \frac{3 l}{4} \cos θ \\ V_{t} = \frac{3 l}{4} ω \cos θ \end{array}$

Conservación del momento angular

El momento de las fuerzas respecto del punto P es nulo (La tensión T tiene como origen P), el momento angular respecto de P se mantiene constante

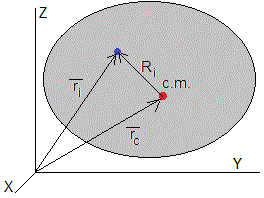
Vamos a demostrar que el momento angular respecto de P es la suma del momento angular del centro de masas y del momento angular de rotación alrededor de un eje que pasa por el c.m.

Posición y velocidad de la partícula i

$\begin{array}{l} {\vec{r}}_{i} = \vec{r_{c}} + \vec{R_{i}} \\ \vec{v_{i}} = \vec{V_{c}} + \vec{ω} \times \vec{R_{i}} \end{array}$

Centro de masas de un sistema de partículas

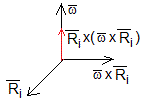
$\begin{array}{l} \vec{r_{c}} = \frac{\sum m_{i} \vec{r_{i}}}{\sum m_{i}} = \frac{\sum m_{i} \vec{r_{i}}}{M} \\ \sum m_{i} \vec{R_{i}} = 0 \end{array}$

Momento angular

$\begin{array}{l} \vec{L} = \sum m_{i} ({\vec{r}}_{i} \times \vec{v_{i}}) = \sum m_{i} ((\vec{r_{c}} + \vec{R_{i}}) \times (\vec{V_{c}} + \vec{ω} \times \vec{R_{i}})) = \\ (\vec{r_{c}} \times \vec{V_{c}}) \sum m_{i} + \vec{r_{c}} \times \vec{ω} \times (\sum m_{i} \vec{R_{i}}) + \vec{V_{c}} \times (\sum m_{i} \vec{R_{i}}) + \sum m_{i} (\vec{R_{i}} \times (\vec{ω} \times \vec{R_{i}})) = \\ \vec{L} = M (\vec{r_{c}} \times \vec{V_{c}}) + (\sum m_{i} R_{i}^{2}) \vec{ω} \\ \vec{L} = M (\vec{r_{c}} \times \vec{V_{c}}) + I_{c m} \vec{ω} \end{array}$

El momento angular inicial de la bala respecto de P es

$L_{P} = m v_{0} l$

El momento angular final respecto de P es

$\begin{array}{l} L_{P} = (2 m) x_{c} V_{y} + I_{c m} ω \\ L_{P} = (2 m) (\frac{3}{4} l) V_{y} + \frac{5}{24} m l^{2} ω \end{array}$

V_y es la componente de la velocidad de traslación del centro de masas

$\begin{array}{l} V_{y} = \vec{V} \cdot \hat{j} = \vec{V} = (V_{t} \hat{t} + V_{n} \hat{n}) \cdot \hat{j} = V_{t} \cos θ + V_{n} \sin θ = (\frac{3 l}{4} ω \cos θ) \cos θ + (\frac{3 l}{4} ω \sin θ - u) \sin θ \\ V_{y} = \frac{3 l}{4} ω - u \sin θ \end{array}$

La conservación del momento angular es

$\begin{array}{l} m v_{0} l = (2 m) (\frac{3}{4} l) V_{y} + \frac{5}{24} m l^{2} ω \\ v_{0} = \frac{3}{2} (\frac{3 l}{4} ω - u \sin θ) + \frac{5}{24} l ω \end{array}$

Tenemos dos relaciones

$\begin{array}{l} \frac{1}{2} v_{0} \sin θ = \frac{3 l}{4} ω \sin θ - u \\ v_{0} = \frac{3}{2} (\frac{3 l}{4} ω - u \sin θ) + \frac{5}{24} l ω \end{array}$

Con los datos de θ y v₀ despejamos u y la velocidad angular ω

$\begin{array}{l} \cos θ = \frac{1}{3}, \sin θ = \frac{2}{3} \sqrt{2} \\ {\begin{cases} \frac{1}{2} v_{0} \frac{2 \sqrt{2}}{3} = \frac{3 l}{4} ω \frac{2 \sqrt{2}}{3} - u \\ v_{0} = \frac{3}{2} (\frac{3 l}{4} ω - u \frac{2 \sqrt{2}}{3}) + \frac{5}{24} l ω \end{cases} \\ ω = \frac{v_{0}}{l}, u = \frac{\sqrt{2}}{6} v_{0} \end{array}$

Impulso lineal e impulso angular

El impulso lineal lo descomponemos en dos, a lo largo del eje X (varilla) y a lo largo del eje Y

$\begin{array}{l} {\begin{cases} \int_{0}^{Δ t} T_{y} d t = (2 m) V_{y} - m v_{0} \\ \int_{0}^{Δ t} T_{x} d t = (2 m) V_{x} \end{cases} \\ {\begin{cases} J \cos θ = (2 m) V_{y} - m v_{0}, J = \int_{0}^{Δ t} T d t \\ - J \sin θ = (2 m) V_{x} \end{cases} \end{array}$

El impulso angular es

$\begin{array}{l} - \int_{0}^{Δ t} (T_{y} x_{c}) d t + m v_{0} (l - x_{c}) = I_{c m} ω \\ - J \frac{3 l}{4} \cos θ + m v_{0} \frac{l}{4} = \frac{5}{24} m l^{2} ω \end{array}$

Ya hemos calculado la velocidad del punto P (extremo izquierdo de la varilla). De otra forma

$\begin{array}{l} \vec{v_{P}} = \vec{V} + \vec{ω} \times (\vec{r_{P}} - \vec{r_{c m}}) \\ - u (\cos θ \hat{i} + \sin θ \hat{j}) = V_{x} \hat{i} + V_{y} \hat{j} + | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 0 & ω \\ - x_{c} & 0 & 0 \end{matrix} | \\ {\begin{cases} - u \cos θ = V_{x} \\ - u \sin θ = V_{y} - \frac{3 l}{4} ω \end{cases} \end{array}$

Con los datos de θ y v₀ despejamos u y el impulso J de la tensión T

$\begin{array}{l} {\begin{cases} J \cos θ = (2 m) (\frac{3 l}{4} ω - u \sin θ) V_{y} - m v_{0} \\ - J \sin θ = (2 m) (- u \cos θ) \end{cases} \\ \cos θ = \frac{1}{3}, \sin θ = \frac{2}{3} \sqrt{2} \\ {\begin{cases} \frac{1}{3} J = (2 m) (\frac{3 l}{4} ω - u \frac{2}{3} \sqrt{2}) - m v_{0} \\ - \frac{2}{3} \sqrt{2} J = (2 m) (- \frac{1}{3} u) \end{cases} \\ J = \frac{m u}{\sqrt{2}}, v_{0} = \frac{3 l}{2} ω - \frac{3 \sqrt{2}}{2} u \end{array}$

Sustituimos en la ecuación del impulso angular

$\begin{array}{l} - \frac{m u}{\sqrt{2}} \frac{3 l}{4} \frac{1}{3} + m v_{0} \frac{l}{4} = \frac{5}{24} m l^{2} (v_{0} + \frac{3 \sqrt{2}}{2} u) \frac{2}{3 l} \\ - \frac{u}{\sqrt{2}} + v_{0} = \frac{5}{3} (v_{0} + \frac{3 \sqrt{2}}{2} u) \frac{1}{3} \\ u = \frac{v_{0}}{3 \sqrt{2}} = \frac{\sqrt{2}}{6} v_{0}, J = \frac{m}{\sqrt{2}} \frac{v_{0}}{3 \sqrt{2}} = \frac{1}{6} m v_{0} \end{array}$

Otras incógnitas son, la velocidad del centro de masas, o sus componentes V_x y V_y, y la velocidad angular de rotación ω

$\begin{array}{l} \frac{3 l}{2} ω = v_{0} + \frac{3 \sqrt{2}}{2} u = v_{0} + \frac{3 \sqrt{2}}{2} \frac{v_{0}}{3 \sqrt{2}}, ω = \frac{v_{0}}{l} \\ {\begin{cases} V_{x} = - u \cos θ = - \frac{v_{0}}{3 \sqrt{2}} \frac{1}{3} = - \frac{v_{0}}{9 \sqrt{2}} \\ V_{y} = \frac{3 l}{4} ω - u \sin θ = \frac{3 l}{4} \frac{v_{0}}{l} - \frac{v_{0}}{3 \sqrt{2}} \frac{2}{3} \sqrt{2} = \frac{19}{36} v_{0} \end{cases} \end{array}$

Segunda ley de Newton

La aplicación de la segunda ley de Newton nos permite calcular la tensión T de la cuerda

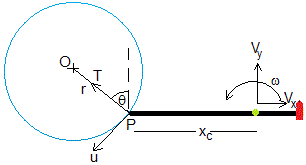
El punto P describe un movimiento circular alrededor del punto fijo O, la sujeción del extremo de la cuerda tensa

La aceleración centrípeta es paralela al vector unitario $\hat{t}$

$\frac{d \vec{v_{P}}}{d t} = \frac{u^{2}}{r} \hat{t}$

La velocidad del punto P es

$\vec{v_{P}} = \vec{V} + \vec{ω} \times (\vec{r_{P}} - \vec{r_{c m}}) = \vec{V} + \vec{ω} \times \vec{r_{P c}}$

Derivamos respecto del tiempo, teniendo en cuenta que el vector $\vec{r_{P c}}$ , tiene longitud fija

$\begin{array}{l} \frac{d \vec{v_{P}}}{d t} = \frac{d \vec{V}}{d t} + \frac{d \vec{ω}}{d t} \times \vec{r_{P c}} + \vec{ω} \times \frac{d \vec{r_{P c}}}{d t} \\ \frac{d \vec{v_{P}}}{d t} = \frac{d \vec{V}}{d t} + \frac{d \vec{ω}}{d t} \times \vec{r_{P c}} + \vec{ω} \times (\vec{ω} \times \vec{r_{P c}}), \vec{r_{P c}} = - x_{c} \hat{i} = - \frac{3 l}{4} \hat{i} \end{array}$

Calculamos las aceleraciones

Aceleración del centro de masa

La aceleración del centro de masa es el cociente entre la fuerza externa T sobre el sistema (varilla-bala) y la masa 2m

$\frac{d \vec{V}}{d t} = \frac{T}{2 m} \hat{t}$

La dirección es la de la cuerda, vector unitario $\hat{t}$

Aceleración angular, $\frac{d \vec{ω}}{d t}$

El momento de a fuerzas externas es igual al momento de inercia por la aceleración angular

$\vec{M} = - T \cos θ \cdot x_{c} \hat{k} = - \frac{3 l}{4} T \cos θ \hat{k}$

El momento de inercia respecto de un eje perpendicular al plano horizontal que pasa por el centro de masa ya se ha calculado

$I_{c m} = \frac{1}{12} m l^{2} + m {(x_{c} - \frac{l}{2})}^{2} + m {(l - x_{c})}^{2} = \frac{5}{24} m l^{2}$

Aplicamos la ecuación de la dinámica de rotación

$\begin{array}{l} \vec{M} = I_{c m} \frac{d \vec{ω}}{d t} \\ - \frac{3 l}{4} T \cos θ \hat{k} = \frac{5}{24} m l^{2} \frac{d \vec{ω}}{d t} \\ \frac{d \vec{ω}}{d t} = - \frac{18}{5} \frac{T \cos θ}{m l} \hat{k} \end{array}$

Aceleración centrífuga

$\vec{ω} \times (\vec{ω} \times \vec{r_{P c}}) = ω \hat{k} \times (ω \hat{k} \times (- x_{c} \hat{i})) = ω \hat{k} \times (- x_{c} ω \hat{j}) = ω^{2} x_{c} \hat{i}$

Reunimos todos los términos

$\begin{array}{l} \frac{d \vec{v_{P}}}{d t} = \frac{d \vec{V}}{d t} + \frac{d \vec{ω}}{d t} \times (- x_{c} \hat{i}) + ω^{2} x_{c} \hat{i} \\ \frac{u^{2}}{r} \hat{t} = \frac{T}{2 m} \hat{t} - \frac{18}{5} \frac{T \cos θ}{m l} \hat{k} \times (- \frac{3 l}{4} \hat{i}) + \frac{3 l}{4} ω^{2} \hat{i} \\ \frac{u^{2}}{r} \hat{t} = \frac{T}{2 m} \hat{t} + \frac{18}{5} \frac{T \cos θ}{m l} \frac{3 l}{4} \hat{j} + \frac{3 l}{4} ω^{2} \hat{i} \end{array}$

Multiplicamos por el vector unitario $\hat{t}$

$\begin{array}{l} \frac{u^{2}}{r} \hat{t} \cdot \hat{t} = \frac{T}{2 m} \hat{t} \cdot \hat{t} + \frac{18}{5} \frac{T \cos θ}{m l} \frac{3 l}{4} \hat{j} \cdot \hat{t} + \frac{3 l}{4} ω^{2} \hat{i} \cdot \hat{t} \\ \frac{u^{2}}{r} = \frac{T}{2 m} + \frac{18}{5} \frac{T \cos θ}{m l} \frac{3 l}{4} \cos θ - \frac{3 l}{4} ω^{2} \sin θ \\ \frac{T}{m} = \frac{\frac{u^{2}}{r} + \frac{3 l}{4} ω^{2} \sin θ}{\frac{1}{2} + \frac{27}{10} \cos^{2} θ} \end{array}$

Conocido el ángulo θ, u y la velocidad angular ω, determinamos la tensión T

$\begin{array}{l} \cos θ = \frac{1}{3}, \sin θ = \frac{2}{3} \sqrt{2}, u = \frac{\sqrt{2}}{6} v_{0}, ω = \frac{v_{0}}{l} \\ \frac{T}{m} = \frac{\frac{1}{18} \frac{v_{0}^{2}}{r} + \frac{3 l}{4} \frac{v_{0}^{2}}{l^{2}} (\frac{2}{3} \sqrt{2})}{\frac{1}{2} + \frac{27}{10} \frac{1}{9}} = \frac{5}{4} (\frac{1}{18 r} + \frac{\sqrt{2}}{2 l}) v_{0}^{2} \end{array}$

Referencias

Vivek Lohani, Nishant Abhangi, Sitikantha Das, Amitabh Virmani. A Jarring Bullet: An Indian National Physics Olympiad 2020 Problem. Resonance. August 2021, pp. 1153-1168