Una pelota que rebota en el suelo
Choque elástico
Consideremos una pelota de masa m y radio R, su momento de inercia es es I=γmR2 respecto de un eje que pasa por el centro y es perpendicular al plano de la trayectoria (de la figura) del centro de masas.
Inmediatamente antes del choque, el centro de la pelota tiene una velocidad cuya componente horizontal es V0x y cuya componente vertical es V0y. La velocidad angular de rotación de la pelota es ω0.
Inmediatamente después del choque, el centro de la pelota tendrá una velocidad cuya componente horizontal es V1x y cuya componente vertical es V1y. La velocidad angular de rotación de la pelota será ω1.
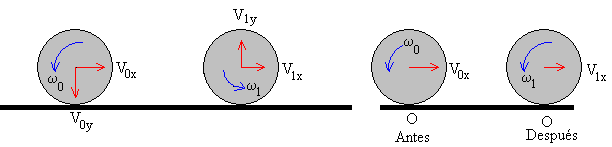
Supondremos que:
La componente vertical de la velocidad no cambia de módulo pero cambia de sentido después del choque.
En el momento del choque, la fuerza que ejerce la pared sobre la pelota actúa en el punto de contacto O. Por lo que el momento angular de la pelota respecto de dicho punto permanece constante.
Se conserva la energía cinética (choque elástico)
V1y=-V0y
Despejamos V1x y ω1 en el sistema de dos ecuaciones con dos incógnitas
Después del primer choque, obtenemos V1x y Rω1 en términos de las velocidades iniciales V0x y Rω0
(1)
Choque inelástico
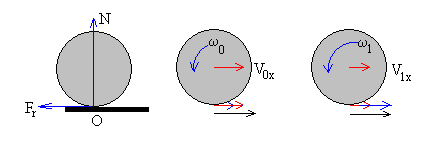
Como consecuencia de la conservación de la energía cinética en un choque elástico.
El cambio en la velocidad del punto de contacto de la pelota con la superficie horizontal es el análogo tangencial del cambio en la velocidad perpendicular a la superficie de la bola durante el rebote
V1y=-V0y
En una colisión inelástica la conservación de la energía no se puede aplicar. Para dar cuenta de las pérdidas de energía asociadas con el cambio de velocidad en la dirección perpendicular a la superficie, se introduce el coeficiente de restitución normal ε
V1y=-εV0y
Donde 0≤ε≤1. La introducción de este coeficiente de restitución sugiere una modificación similar para el cambio de la velocidad en la dirección tangencial.
V1x+ω1R=-β(V0x+ω0R)
Donde -1≤β≤1 es el coeficiente de restitución tangencial.
La introducción de este coeficiente de restitución es una forma simplificada de describir el deslizamiento del punto de contacto de la pelota con la superficie horizontal, tal como veremos con detalle en las próximas páginas y en la sección movimiento general de un sólido rígido.
Como las fuerzas que actúan sobre la bola son la fuerza normal N y la fuerza de rozamiento Fr y ambas pasan por el punto de contacto O, el momento angular respecto de este punto se conserva. Por tanto, las ecuaciones que describen el choque inelástico de una pelota con una pared horizontal son
V1y=-εV0y
V1x+ω1R=-β(V0x+ω0R)
V1x- V0x=-γR(ω0- ω1)
Después del primer choque, obtenemos V1x y Rω1 en términos de las velocidades iniciales V0x y Rω0
Caso particular
Cuando β=1 y ε=1, las ecuaciones se reducen al choque elástico.
Una situación particular interesante se produce cuando la velocidad V1x después del choque con el suelo es igual y de sentido contrario a la velocidad inicial antes del choque V0x.
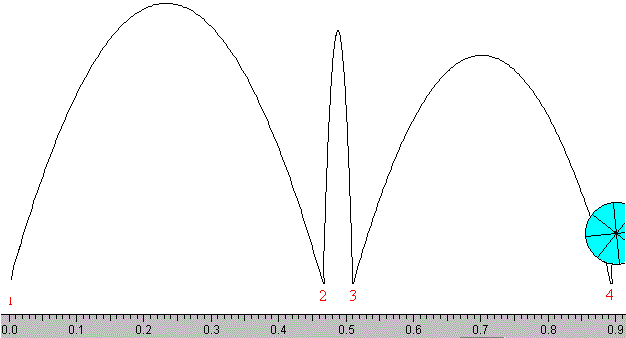
En la figura, se muestra la trayectoria del centro de la pelota cuando β=1, ε=1, V0x=1.0, Rω0=5/2. La pelota rebota en dos posicones situadas a uno y otro lado del origen.
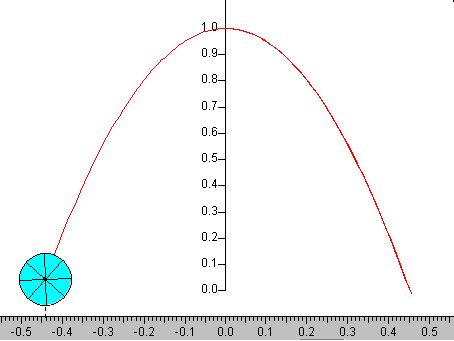
Ejemplo.
- Coeficiente de restitución normal, ε=0.95
- Coeficiente de restitución tangencial, β=0.9
- Se deja caer la pelota desde una altura de h=1 m, partiendo del reposo V0x=0.0.
- La velocidad angular inicial de rotación es ω0R=-1.0
- La pelota es una esfera homogénea de radio R, por lo que γ=2/5
Velocidad de la pelota al llegar al suelo
Velocidades
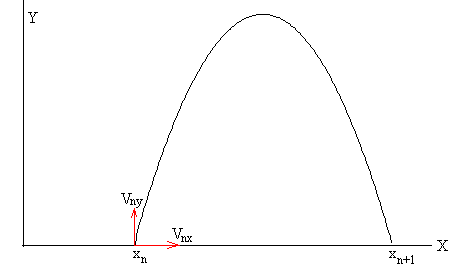
Ecuaciones del tiro parabólico
Retorna al suelo cuando y=0, la posición del próximo n+1 rebote es
En la siguiente tabla figuran los resultados del cálculo
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Vy | 4.21 | 4.0 | 3.8 | 3.61 | 3.43 |
| Vx | 0.54 | 0.05 | 0.49 | 0.1 | 0.45 |
| Rω | 0.36 | -0.846 | 0.24 | -0.75 | 0.14 |
| x | 0 | 0.47 | 0.51 | 0.89 | 0.97 |
Actividades
Se introduce
- El coeficiente de restitución normal ε, en el control titulado Restitución.
- El coeficiente de restitución tangencial β, en el control titulado Coef. beta.
- La velocidad angular inicial de rotación ω0R, en el control titulado Rotación ω·R
- La altura inicial desde la que se deja caer la pelota se ha fijado en h=1.0 m
- La pelota es una esfera homogénea cuyo momento de inercia es I=(2/5)mR2, por lo que γ=2/5.
Se pulsa el botón titulado Nuevo
Observar la trayectoria seguida por el centro de la pelota, y calcular las posiciones xn de rebote.
Referencias
Hefner B. T. The kinematics of a superball bouncing between two vertical surfaces. Am. J. Phys. 72 (7) July 2004, pp. 875-883

