Comenzaremos con una aplicación del principio de conservación del momento angular

Un disco de masa m_d y radio R, puede girar con velocidad angular ω₀ alrededor de un eje perpendicular al plano del disco y que pasa por su centro.

Tiene un dispositivo situado a una distancia r del eje que dispara un proyectil de masas m con velocidad u (relativa al disco) haciendo un ángulo θ con la dirección radial.

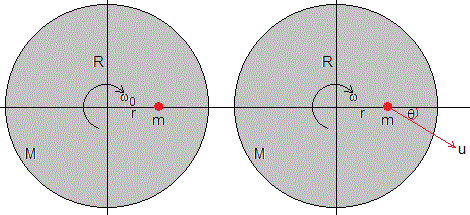
Calcular la velocidad angular ω del disco inmediatamente después del disparo

Tomamos el sentido de las agujas del reloj como positivo.

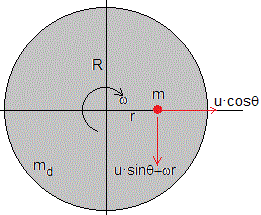
El momento angular inicial es

${\displaystyle L=\left(\frac{1}{2}{m}_d{R}^2+m{r}^2\right){\omega }_0}$

En la figura, se muestra las componentes de la velocidad del proyectil respecto del laboratorio

El momento angular final

${\displaystyle L=\left(\frac{1}{2}{m}_d{R}^2\right)\omega +mr\left(u+\omega r\sin \theta \right)}$

Igualando el momento angular inicial al final, despejamos la velocidad angular ω final

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_d{R}^2+m{r}^2\right){\omega }_0=\left(\frac{1}{2}{m}_d{R}^2\right)\omega +mr\left(u\sin \theta +\omega r\right)\\ \omega ={\omega }_0-\frac{mru\sin \theta }{\frac{1}{2}{m}_d{R}^2+m{r}^2}\end{array}}$

El disco se frena. El ángulo θ=90°, es el óptimo para que se frene el disco. En cambio, si θ=0° el disco no disminuye su velocidad. Por otra parte, la distancia r=R, situando el dispositivo en el borde del disco, es la opción mas favorable

${\displaystyle \omega ={\omega }_0-\frac{m}{\frac{1}{2}{m}_d+m}\frac{u}{R}}$

Actividades

Se introduce

• El ángulo θ de la velocidad del proyectil respecto de la dirección radial, en el control titulado Angulo
• La velocidad u de disparo, respecto del disco, en el control titulado Velocidad
• El cociente m_d/m entre la masa del disco y la del proyectil, en el control titulado Cociente
• La distancia r del dispositivo de disparo al eje del disco, en el control titulado Distancia
• El radio del disco se ha fijado, R=1 m
• La velocidad angular inicial, se ha fijado en ω₀= 1 rad/s

Se pulsa el botón titulado Nuevo

En la parte superior izquierda, se proporciona el dato de la velocidad angular final del disco ω

Formulación discreta de las ecuación del movimiento del cohete

Un cohete en rotación, expulsa una fracción m de su combustible a intervalos de tiempos fijos (por ejemplo, cada segundo), con una velocidad u respecto del cohete. Consideraremos que la velocidad u es constante en el sistema de referencia que se mueve con el cohete

Para calcular la velocidad angular del cohete a medida que va expulsando el combustible aplicamos el principio de conservación del momento angular.

• Primer disparo



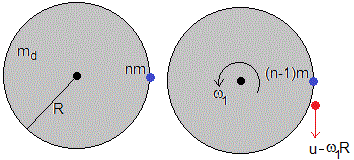
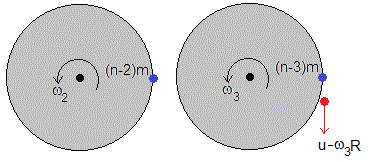
En el borde del disco de masa m_d y radio R, hay n proyectiles de masa m cada uno, que se van disparando con velocidad u relativa al disco en la dirección perpendicular a la radial

En la figura, se muestra la situación inicial y final tras el primer disparo. Aplicando el principio de conservación del momento angular

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_d{R}^2+\left((n-1)m\right)R^2\right){\omega }_1+mR\left(R{\omega }_1-u\right)=0\\ {\omega }_1=\frac{m}{\frac{1}{2}{m}_d+n·m}\frac{u}{R}=\frac{m}{M_0}\frac{u}{R}\end{array}}$

Donde M₀=m_d/2+n·m

• Segundo disparo



${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_d{R}^2+\left((n-2)m\right)R^2\right){\omega }_2+mR\left(R{\omega }_2-u\right)=\left(\frac{1}{2}{m}_d{R}^2+\left((n-1)m\right)R^2\right){\omega }_1\\ \left(\frac{1}{2}{m}_d{R}^2+\left((n-1)m\right)R^2\right){\omega }_2-mRu=\left(\frac{1}{2}{m}_d{R}^2+\left((n-1)m\right)R^2\right){\omega }_1\\ {\omega }_2={\omega }_1+\frac{m}{M_0-m}\frac{u}{R}=\frac{m}{M_0}\frac{u}{R}+\frac{m}{M_0-m}\frac{u}{R}\\ {\omega }_2=m\frac{u}{R}\left(\frac{1}{M_0}+\frac{1}{M_0-m}\right)\end{array}}$

• Tercer disparo



${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_d{R}^2+\left((n-3)m\right)R^2\right){\omega }_3+mR\left(R{\omega }_3-u\right)=\left(\frac{1}{2}{m}_d{R}^2+\left((n-2)m\right)R^2\right){\omega }_2\\ \left(\frac{1}{2}{m}_d{R}^2+\left((n-2)m\right)R^2\right){\omega }_3-mRu=\left(\frac{1}{2}{m}_d{R}^2+\left((n-2)m\right)R^2\right){\omega }_2\\ {\omega }_3={\omega }_2+\frac{m}{M_0-2m}\frac{u}{R}=\frac{u}{R}\left(\frac{m}{M_0}+\frac{m}{M_0-m}\right)+\frac{m}{M_0-2m}\frac{u}{R}\\ {\omega }_3=m\frac{u}{R}\left(\frac{1}{M_0}+\frac{1}{M_0-m}+\frac{1}{M_0-2m}\right)\end{array}}$

• Ultimo disparo, n. Velocidad angular final del disco

${\displaystyle \begin{array}{l}{\omega }_n=m\frac{u}{R}\left(\frac{1}{M_0}+\frac{1}{M_0-m}+\frac{1}{M_0-2m}+\mathrm{...}+\frac{1}{M_0-\left(n-1\right)m}\right)\\ {\omega }_n=m\frac{u}{R}{\displaystyle \sum _{i=1}^n\frac{1}{M_0-\left(i-1\right)m}}\end{array}}$

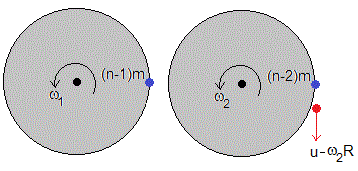
De la descripción discreta a la continua.

Podemos escribir, la velocidad angular final ω_n de esta forma más conveniente

${\displaystyle {\omega }_n=m\frac{u}{R}{\displaystyle \sum _{i=1}^n\frac{1}{M_0-nm+im}}=\frac{u}{R}{\displaystyle \sum _{i=1}^n\frac{m}{M_f+im}}}$

Donde M_f=m_d/2

En el límite, cuando el cohete pierde masa de forma continua, n es grande y m es una cantidad infinitesimal, por ejemplo, dx. La velocidad angular final es

${\displaystyle \omega =\frac{u}{R}{\displaystyle \underset{0}{\overset{M_0-M_f}{\int }}\frac{dx}{M_f+x}}=\frac{u}{R}\ln \left(\frac{M_0}{M_f}\right)}$

La diferencia entre M₀ y M_f es el combustible quemado por el cohete

Un cohete de empuje constante

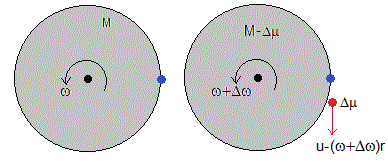
Consideremos un cohete de masa inicial M que lleva una velocidad angular ω. En el instante t+Δt, se expulsa una masa Δμ con una velocidad constante u relativa al cohete, como consecuencia la masa restante (M-Δμ) del cohete se incrementa su velocidad angular en ω+Δω.

${\displaystyle \begin{array}{l}L(t)=\left(\frac{1}{2}{m}_d+m\right)R^2\omega \\ L(t+\Delta t)=\left(\frac{1}{2}{m}_d+m-\Delta \mu \right)R^2\left(\omega +\Delta \omega \right)+R·\Delta \mu \left(R\left(\omega +\Delta \omega \right)-u\right)=\\ \left(\frac{1}{2}{m}_d+m\right)R^2\omega +\left(\frac{1}{2}{m}_d+m\right)R^2\Delta \omega -R^2\omega \Delta \mu +R^2\omega \Delta \mu +R^2\Delta \mu ·\Delta \omega -uR·\Delta \mu =\\ \left(\frac{1}{2}{m}_d+m\right)R^2\omega +\left(\frac{1}{2}{m}_d+m\right)R^2\Delta \omega -uR·\Delta \mu \end{array}}$

Se ha despreciado el producto Δμ·Δω

El momento angular en el instante t es igual al momento angular en el instante t+Δt

${\displaystyle \Delta L=L(t+\Delta t)-L(t)=\left(\frac{1}{2}{m}_d+m\right)R^2\Delta \omega -uR·\Delta \mu =0}$

En el límite cuando Δt→0

${\displaystyle M\frac{d\omega }{dt}-\frac{u}{R}\frac{d\mu }{dt}=0}$

La masa del sistema formado por el cohete M y el combustible expulsado μ es constante M₀=M+μ, por lo que dμ+dM=0. La masa del cohete disminuye en dM y aumenta la masa del combustible expulsado en la misma cantidad.

${\displaystyle M\frac{d\omega }{dt}+\frac{u}{R}\frac{dM}{dt}=0}$

Eliminando dt de la ecuación diferencial

${\displaystyle \begin{array}{l}d\omega =-\frac{u}{R}\frac{dM}{M}\\ \omega =-\frac{u}{R}{\displaystyle \underset{M_0}{\overset{M_f}{\int }}\frac{dM}{M}}=-\frac{u}{R}\ln \frac{M_f}{M_0}=\frac{u}{R}\ln \frac{M_0}{M_f}\end{array}}$

Obtenemos el mismo resultado que con la formación discreta

Referencias

Carl E Mungan. The rotational rocket. Phys. Educ. 58 (2023) 033001