Transferencia de la velocidad en un choque por medio de una varilla interpuesta (I)

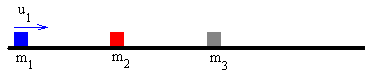
La máxima transferencia de velocidad entre la primera y la tercera partícula se produce cuando la partícula intermedia tiene una masa $m_{2} = \sqrt{m_{1} m_{3}}$

Conservación del momento angular

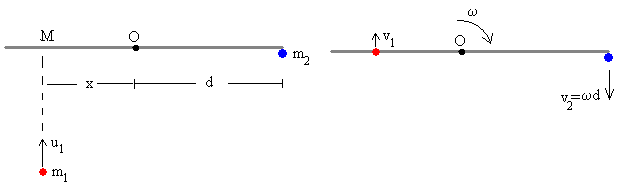
En la figura, observamos el dispositivo antes del choque. Una partícula de masa m₁ que lleva una velocidad constante u₁ choca contra una varilla de masa M y de longitud 2d que está inicialmente en reposo y que puede girar alrededor de un eje fijo, perpendicular a la varilla y que pasa por su centro. Una partícula de masa m₂ permanece en reposo en el extremo de la varilla.

Al chocar la partícula de masa m₁ con la varilla a una distancia x de su eje, la varilla gira y mueve a la partícula de masa m₂. La varilla es el mecanismo intermedio que permite transferir parte de la energía de la primera partícula a la segunda

El sistema formado por las dos partículas y la varilla no es aislado, ya que la varilla está sujeta por su eje central. El momento de las fuerzas exteriores respecto del eje de rotación O es nulo, por lo que se conserva el momento angular

$\frac{d \vec{L}}{d t} = \vec{M_{e x t}} \vec{M_{e x t}} = 0 \vec{L} = cte$

Antes del choque la varilla y la partícula de masa m₂ están en reposo. El momento angular inicial respecto de O es

L_i=m₁u₁·x

Después de la colisión, la partícula incidente se mueve con velocidad v₁, la velocidad angular de rotación de la varilla es ω, y la velocidad de la segunda partícula es v₂=ω·d. El momento angular final respecto de O es

$L_{f} = m_{1} v_{1} \cdot x + m_{2} v_{2} \cdot d + \frac{1}{3} M d^{2} ω$

El momento de inercia de la varilla respecto de su eje central es M(2d)²/12=Md²/3.

La conservación del momento angular nos proporciona la primera ecuación

$m_{1} u_{1} \cdot x = m_{1} v_{1} \cdot x + m_{2} ω d^{2} + \frac{1}{3} M d^{2} ω$

La definición de coeficiente de restitución e, aplicada al choque entre la primera partícula y un punto de la varilla situado a una distancia x del eje de rotación, nos proporciona la segunda ecuación.

v₁-ωx=-e(u₁-0)

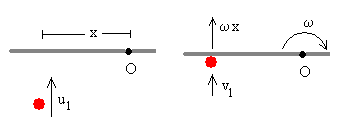
Despejamos la velocidades después del choque v₁ y v₂

$\begin{array}{l} v_{2} = ω d = \frac{(1 + e) m_{1} \cdot x \cdot d}{m_{1} x^{2} + m_{2} d^{2} + M d^{2} / 3} u_{1} \\ v_{1} = ω x - e u_{1} = \frac{m_{1} \cdot x^{2} - e m_{2} d^{2} - e M d^{2} / 3}{m_{1} x^{2} + m_{2} d^{2} + M d^{2} / 3} u_{1} \end{array}$

La no conservación del momento lineal

Si la masa de la varilla es despreciable M=0

$v_{2} = \frac{(1 + e) \cdot m_{1} x d}{m_{1} x^{2} + m_{2} d^{2}} u_{1} v_{1} = \frac{m_{1} x^{2} - e m_{2} d^{2}}{m_{1} x^{2} + m_{2} d^{2}} u_{1}$

Comprobamos haciendo algunas operaciones, que se cumple la siguiente relación entre los momentos de las partículas antes y después del choque.

$\frac{d}{x} m_{2} v_{2} + m_{1} v_{1} = m_{1} u_{1}$

Como vemos no se conserva el momento lineal en la colisión, incluso si la masa de la varilla es despreciable.

Máxima transferencia de la velocidad en el choque

La máxima transferencia de velocidad no se produce para x=d cuando el brazo del momento angular es máximo como cabría esperar a primera vista.

La transferencia máxima de velocidad se realiza para un valor de x tal que hace que la velocidad v₂ de la segunda partícula después del choque sea máxima. Derivando v₂ respecto de x e igualando a cero obtenemos

$\frac{d v_{2}}{d x} = 0 m_{1} x^{2} = m_{2} d^{2} + \frac{1}{3} M d^{2}$

Las velocidades de las partículas después del choque son, respectivamente,

$v_{2} = \frac{(1 + e) d}{2 x} u_{1} v_{1} = \frac{(1 - e)}{2} u_{1}$

En un choque perfectamente elástico e=1, la partícula incidente permanece en reposo v₁=0 después del choque.

En el caso de que la varilla tenga una masa despreciable M=0, el valor de x se obtiene de la relación de proporcionalidad

$\frac{x^{2}}{d^{2}} = \frac{m_{2}}{m_{1}}$

Ejemplos

Choque elástico y varilla de masa despreciable

Masa de la varilla M=0
Masa de la partícula m₂=0.25 kg
Coeficiente de restitución e=1.
Masa de la partícula incidente m₁=1 kg
Velocidad inicial de la partícula incidente u₁=1 m/s
Posición de la partícula incidente x=0.5.

Observamos que

la partícula incidente queda en reposo después del choque, v₁=0
la segunda partícula adquiere una velocidad de v₂=2 m/s.

Toda la energía de la partícula incidente se ha convertido en energía cinética de la segunda partícula. Como la varilla no tiene masa, su energía de rotación es cero.

Choque inelástico y varilla de masa despreciable

Masa de la varilla M=0
Masa de la partícula m₂=0.25
Coeficiente de restitución e=0.8.
Masa de la partícula incidente m₁=1 kg
Velocidad inicial de la partícula incidente u₁=1 m/s
Posición de la partícula incidente x=0.5.

Observamos que

La velocidad de la partícula incidente después del choque es v₁=0.1 m/s
La velocidad de la segunda partícula después del choque es, v₂=1.8 m/s

Comprobamos la relación ente los momentos inicial y final de las partículas

$\frac{1}{0.5} 0.25 \cdot 1.8 + 1 \cdot 0.1 = 1 \cdot 1$

Una parte de la energía de la partícula incidente se ha convertido en energía cinética de la segunda partícula, otra parte, se ha perdido en el choque, y el resto es la energía cinética de la primera partícula después del choque. Como la varilla no tiene masa, su energía de rotación es cero.

La partícula incidente permanece en reposo para un valor de x tal que

m₁·x²=e·m₂d²

Con estos datos para x=0.447≈0.45, la partícula incidente permanece en reposo después del choque, v₁=0.

La velocidad de la segunda partícula después del choque es v₂=1.61 m/s, que como apreciamos no corresponde a la máxima transferencia de velocidad.

Una parte de la energía de la partícula incidente se ha convertido en energía cinética de la segunda partícula, el resto se ha perdido en el choque.

Choque elástico y masa de la varilla no nula.

Masa de la varilla M=1.5 kg
Masa de la partícula m₂=0.25
Coeficiente de restitución e=1.0.
Masa de la partícula incidente m₁=1 kg
Velocidad inicial de la partícula incidente u₁=1 m/s
Posición de la partícula incidente x=0.866.

La máxima transferencia de velocidad se produce para esta posición

La partícula incidente después del choque permanece en reposo v₁=0 m/s
La velocidad de la segunda partícula después del choque es, v₂=1.155 m/s

La energía de la partícula incidente se ha repartido en energía de rotación de la varilla (en color gris) y energía cinética de la segunda partícula (en color azul).

Actividades

Se introduce

La masa m₂ de la segunda partícula, en el control titulado Masa partícula.
La masa de la varilla M, en el control titulado Masa varilla
El coeficiente de restitución e, en el control titulado Coeficiente de restitución.
La posición de la partícula de color rojo en el control Posición.
La longitud de la varilla 2d se mantiene fija e igual a 2 m.
La masa de la partícula incidente m₁ se mantiene fija e igual a 1 kg
La velocidad u₁ de la partícula incidente se mantiene fija e igual a 1 m/s.

Se pulsa el botón titulado Nuevo

La partícula incidente se mueve hacia la varilla, choca y observamos el movimiento de la partícula incidente (de color rojo) después del choque, la rotación de la varilla y el movimiento de la segunda partícula (de color azul).

En la parte superior izquierda, se nos proporciona los datos relativos a las velocidades de los tres elementos que intervienen antes y después del choque.

En la parte superior derecha, se representa un diagrama en forma de tarta que muestra como se distribuye la energía después del choque entre los tres elementos. Los sectores representan:

La energía cinética de la partícula incidente después del choque $E_{1} = \frac{1}{2} m_{1} v_{1}^{2}$ (en color rojo).
La energía de la segunda partícula $E_{2} = \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} m_{2} ω^{2} d^{2}$ (en color azul).
La energía cinética de rotación de la varilla $E_{3} = \frac{1}{2} (\frac{1}{3} M d^{2}) ω^{2}$

Coeficiente restitución :
Masa varilla (kg) Masa partícula (kg)
Posición

Referencias

MacInnes I. The lever as an impedance matching device. Physics Education, 7, November 1972, pp 509-511.