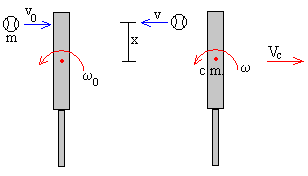
En la figura, se muestra el esquema del choque entre un bate y una pelota de béisbol. La pelota de masa m y velocidad u, choca contra un bate de masa M y de momento de inercia I respecto de un eje que pasa por su centro de masa. V_c es la velocidad final del c.m. de bate, ω y ω₀ son las velocidades angulares inicial y final del bate, x es la distancia desde el c.m. del bate y el punto donde choca la pelota.

Hacemos una primera aproximación, suponiendo que el bate es una varilla rígida delgada de masa M y longitud L que está suspendida libremente e inicialmente en reposo, y la pelota se comporta como una partícula de masa m que lleva una velocidad u, y que choca con el bate a una altura x medida desde su centro de masas.

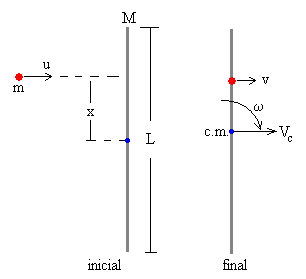
En la figura de la izquierda, se muestra la situación inicial y en la de la derecha la situación final: la partícula lleva una velocidad v, y la varilla describe un movimiento de rotación alrededor de su centro de masas con velocidad angular ω y su centro de masas se traslada con velocidad V_c.

El sistema formado por la partícula y la varilla es aislado, la resultante de las fuerzas exteriores es cero, por lo que son aplicables los principios de conservación del momento lineal y angular.

• Principio de conservación del momento lineal

${\displaystyle \overrightarrow{F_{ext}}=\frac{d\overrightarrow{P}}{dt}\overrightarrow{F_{ext}}=0\overrightarrow{P}=\text{cte}}$

mu=MV_c+mv

• Principio de conservación del momento angular

${\displaystyle \overrightarrow{M_{ext}}=\frac{d\overrightarrow{L}}{dt}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

mu·x=I_cω+mv·x

donde I_c=ML²/12 es momento de inercia de la varilla respecto de un eje perpendicular a la varilla y que pasa por el c.m.

Tenemos dos ecuaciones y tres incógnitas v, ω y V_c.

• El balance energético de la colisión

${\displaystyle \frac{1}{2}m{u}^2+Q=\frac{1}{2}m{v}^2+\frac{1}{2}M{V}_c^2+\frac{1}{2}{I}_c{\omega }^2}$

Es la diferencia entre las energías cinética final e inicial. Q es la energía perdida en la colisión, una cantidad negativa que indica que la energía final es menor que la inicial.

Si el choque es perfectamente elástico Q=0, disponemos de una tercera ecuación que nos permite despejar las tres incógnitas: v, ω y V_c conocida la velocidad u de la partícula incidente. En los demás casos desconocemos el valor de Q.

Definición de coeficiente de restitución

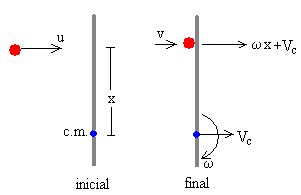
La definición de coeficiente de restitución e nos proporciona la tercera ecuación

Suponemos que la partícula de masa m y velocidad u choca contra una hipotética partícula inicialmente en reposo situada en el bate a una altura x. Después del choque la primera partícula lleva una velocidad v y la segunda una velocidad V_c+ ω·x, la suma de la velocidad de traslación y rotación.

• la velocidad relativa de acercamiento es u-0
• la velocidad relativa de alejamiento es v-(V_c+ ω·x)

El coeficiente de restitución e se define

v-(V_c+ ω·x)=-e(u-0)

Si conocemos el dato del coeficiente de restitución e, disponemos de tres ecuaciones con tres incógnitas. Después de algunas operaciones obtenemos

• La velocidad angular ω de rotación de la varilla alrededor de un eje que pasa por el c.m.

${\displaystyle \omega =\frac{Mmu·x(1+e)}{(M+m)·I_c+mM·x^2}}$  

• La velocidad V_c de traslación del c.m. de la varilla

${\displaystyle V_c=\frac{m(1+e)u-m\omega x}{m+M}}$

• La velocidad v de la partícula después del choque

v=-eu+V_c+ω·x

Choque elástico

• Conservación del momento lineal

mu=MV_c+mv

• Conservación del momento angular

mu·x=I_cω+mv·x

• No hay pérdida de energía en el choque

${\displaystyle \frac{1}{2}m{u}^2=\frac{1}{2}m{v}^2+\frac{1}{2}M{V}_c^2+\frac{1}{2}{I}_c{\omega }^2}$

Despejamos la velocidad del c.m. de la varilla V_c y la velocidad angular de rotación de la varilla ω.

${\displaystyle \omega =\frac{2Mm·x}{(M+m)·I_c+mM·x^2}u{V}_c=\frac{2m{I}_c}{(M+m)·I_c+mM·x^2}u}$

que es el mismo resultado que hemos obtenido anteriormente con el coeficiente de restitución e=1.

La velocidad angular de rotación es

${\displaystyle \omega =\frac{2x}{a+x^2}ua=\left(\frac{M}{m}+1\right)\frac{1}{12}{L}^2}$

El valor máximo de la velocidad angular de rotación ω de la varilla no lo obtenemos cuando el parámetro de impacto es el mayor posible x=L/2. El máximo de la función ω(x) se obtiene para

${\displaystyle x_m=\sqrt{a}=\frac{L}{2}\sqrt{\frac{1}{3}\left(1+\frac{M}{m}\right)}}$

• Si M>2m entonces x_m>L/2 lo que no es posible. La velocidad angular ω crece con x alcanzando el valor mayor cuando x=L/2 (curva de color rojo en la figura).

• Si M<2m entonces el máximo se produce para x_m<L/2, (curva de color azul)

Representamos la función ω(x) para M=2.5m y M=0.5 m.

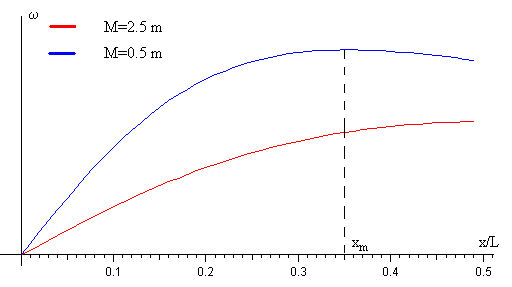
En el segundo caso la función presenta un máximo para

${\displaystyle x_m=\frac{1}{2\sqrt{2}}L=0.35L}$

Ejemplos

• Velocidad inicial de la partícula u=1.0 m/s
• Masa de la partícula m=0.25 kg
• Masa de la varilla M=1.5 kg
• Longitud de la varilla L=1.0 m
• Coeficiente de restitución e=0.7
• Parámetro de impacto de la partícula x=0.3

El momento de inercia de la varilla respecto de un eje perpendicular a la varilla que pasa por su c.m. es

${\displaystyle I_c=\frac{1}{12}M{L}^2=\frac{1}{12}{1.51}^2=0.125{\text{kgm}}^{\text{2}}}$

Ecuaciones

1. Principio de conservación del momento lineal

0.25·1.0=1.5·V_c+0.25·v

2. Principio de conservación del momento angular

0.25·1.0·0.3=0.125ω+0.25v·0.3

3. Coeficiente de restitución

v-(V_c+ ω·0.3)=-0.7(1.0-0)

Resolvemos el sistema de tres ecuaciones con tres incógnitas y calculamos después del choque:

• la velocidad de la partícula  v=-0.262 m/s,
• la velocidad del centro de masas de la varilla  V_c=0.210 m/s,
• la velocidad angular de rotación de la varilla alrededor de un eje perpendicular a la varilla que pasa por su c.m, ω=0.757 rad/s

Balance energético de la colisión

${\displaystyle \begin{array}{l}\frac{1}{2}0.25·{1.0}^2+Q=\frac{1}{2}0.25·{0.262}^2+\frac{1}{2}1.5·{0.210}^2+\frac{1}{2}0.125·{0.757}^2\\ Q=-0.047\text{J}\end{array}}$

Ejemplo 2:

Cambiamos el coeficiente de restitución e=1

v=-0.485 m/s, V_c=0.247 m/s,  ω=0.891 rad/s

Balance energético de la colisión, Q=0 

Actividades

Se introduce

• La masa m de la partícula, en el control titulado Masa partícula.
• La masa de la varilla M, en el control titulado Masa varilla
• El coeficiente de restitución e, en el control titulado Coef. de restitución.
• La longitud de la varilla L se mantiene fija e igual a 1 m.
• La velocidad u de la partícula incidente se mantiene fija e igual a 1 m/s.
• el parámetro de impacto x en el control titulado Distancia.

Se pulsa el botón titulado Nuevo

La partícula incidente se mueve hacia la varilla. Choca y observamos el movimiento de la partícula incidente (de color rojo) después del choque, y el movimiento de traslación y de rotación de la varilla.

En la parte superior derecha, se nos proporciona los datos relativos a las velocidades

• v de la partícula después del choque
• V_c de traslación del c.m. de la varilla
• ω de rotación de la varilla alrededor de un eje que pasa por el c.m.

En la parte inferior izquierda, se representa un diagrama en forma de tarta que muestra como se distribuye la energía después del choque. Los sectores representan:

• La energía cinética de la partícula incidente después del choque $E_1=\frac{1}{2}m{v}^2$ (en color rojo).

• La energía cinética de traslación del c.m. de la varilla $E_2=\frac{1}{2}M{V}_c^2$ (en color azul).

• La energía cinética de rotación de la varilla $E_3=\frac{1}{2}{I}_c{\omega }^2$ (en color gris)

Si el choque es elástico, la energía inicial es igual a la final. Si el choque no es elástico la energía inicial es mayor que la final. Un círculo de mayor radio de color gris claro indica la energía inicial y el de menor radio dividido en sectores la energía final.

Referencias

Cross R. Impact of a ball with a bat or racket. Am. J. Phys. 67 (8) August 1999, pp. 692-694

Lemos N. A. Failure of intuition in elementary rigid body mechanics. Eur. J. Phys. 29 (2008) N1-N4