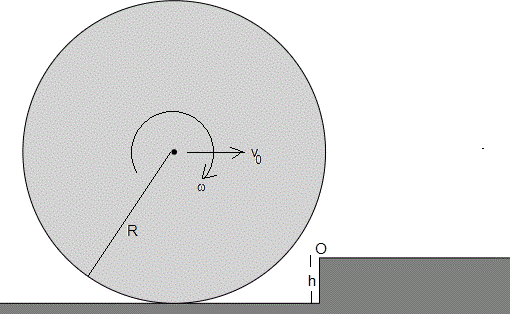
La esfera rueda sin deslizar por el plano horizontal, la velocidad de traslación del centro de masa v₀ y la velocidad angular de rotación ω alrededor de un eje que pasa por el centro de masa están relacionados, v₀=ω·R

La energía inicial de la esfera es la suma de la energía cinética de traslación del centro de masa con velocidad v₀ y la energía cinética de rotación alrededor de un eje que pasa por el centro de masa con velocidad angular, v₀/R

${\displaystyle E_1=\frac{1}{2}m{v}_0^2+\frac{1}{2}\left(\frac{2}{5}m{R}^2\right)\frac{v_0^2}{R^2}=\frac{7}{10}m{v}_0^2}$

Sabiendo que el momento de inercia de una esfera respecto de un eje que pasa por su centro es I_cm=2mR²/5, el momento angular de la esfera (que se traslada y gira) respecto del vértice O en el escalón, es

${\displaystyle L=m{v}_0(R-h)+\left(\frac{2}{5}m{R}^2\right)\omega =\frac{7}{5}m{v}_{0}R-m{v}_{0}h}$

Choque con el escalón

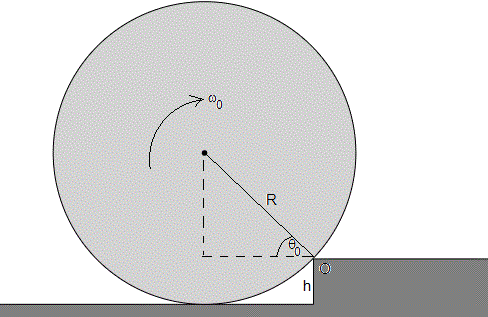
Cuando la esfera choca con el escalón, el centro de la esfera empieza a girar con velocidad angular ω₀ alrededor de un eje perpendicular al plano de la figura y que pasa por el punto de impacto O en el escalón.

Aplicando Steiner, el momento de inercia de la esfera respecto de un eje perpendicular al plano de la figura que para por O es

${\displaystyle I_O=\frac{2}{5}m{R}^2+m{R}^2=\frac{7}{5}m{R}^2}$

El momento angular de la esfera respecto de O es

${\displaystyle L=\frac{7}{5}m{R}^2{\omega }_0}$

Aplicamos el principio de conservación del momento angular ya que el momento de las fuerzas externas aplicadas a la esfera en el punto de impacto son cero. De este modo, obtenemos la velocidad angular inicial de rotación de la esfera alrededor de un eje perpendicular al plano de la figura y que pasa por el punto de impacto O.

${\displaystyle {\omega }_0=\left(1-\frac{5}{7}\frac{h}{R}\right)\frac{v_0}{R}}$

La energía de la esfera después del choque es

${\displaystyle E_2=\frac{1}{2}\left(\frac{7}{5}m{R}^2\right){\omega }_0^2=\frac{7}{10}m{\left(1-\frac{5}{7}\frac{h}{R}\right)}^2{v}_0^2}$

La energía disipada en la colisión es la diferencia ΔE=E₂-E₁

Movimiento de rotación

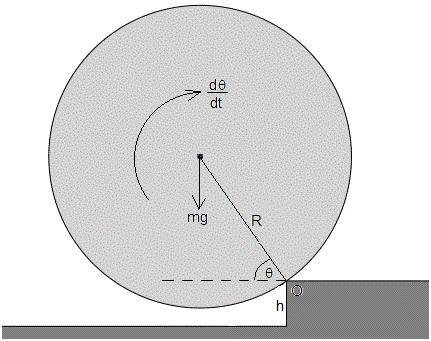
Aplicamos la ecuación de la dinámica de rotación a la esfera en su movimiento de rotación alrededor de un eje perpendicular al plano de la figura y que pasa por O

${\displaystyle \begin{array}{l}\left(\frac{7}{5}m{R}^2\right)\frac{d^2\theta }{d{t}^2}=-mgR\cos \theta \\ \frac{d^2\theta }{d{t}^2}=-\frac{5}{7}\frac{g}{R}\cos \theta \end{array}}$

Integramos esta ecuación diferencial, con las condiciones iniciales siguientes: θ=θ₀, dθ/dt=ω₀.

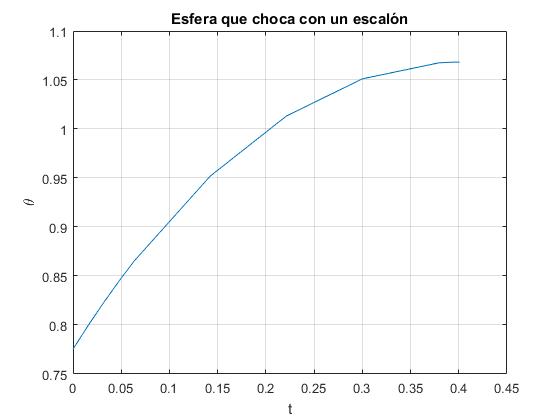
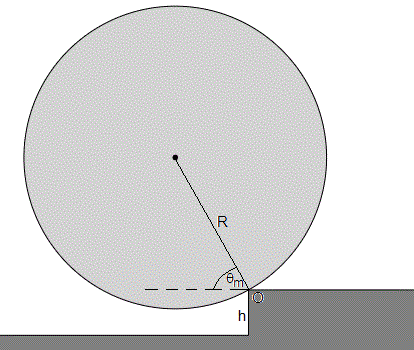
Consideremos una esfera de radio R=1 que se mueve con velocidad v₀=2, choca con un escalón de altura h=0.3. Resolvemos mediante ode45 de MATLAB la ecuación diferencial. La esfera gira alrededor de la esquina del escalón hasta alcanzar la posición angular máxima θ_m=1.07 (61.2°), con velocidad angular cero, regresa a la posición angular de partida θ₀ con la misma velocidad angular ω₀ pero cambiada de signo

h=0.3;  %altura escalón
R=1; %radio esfera
v0=2; %velocidad incial
w0=(1-5*h/(7*R))*v0/R; %velocidad angular inicial
th_0=asin((R-h)/R); %ángulo inicial
x0=[th_0,w0];
f=@(t,x) [x(2); -5*9.8*cos(x(1))/(7*R)]; 
opts=odeset('events',@stop_esfera_escalon);
[t,x, te, xe,ie]=ode45(f,[0,50],x0,opts);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Esfera que choca con un escalón')

En la ventana de comandos, la variable xe nos proporciona la posición angular final y la velocidad angular final

>> xe
xe =    1.0682   -0.0000

La integración numérica de la ecuación diefrencial se detiene cuando la velocidad angular es cero o bien, cuando la posición angular alcanza π/2 (90°) y la esfera continua su movimiento. Definimos la función stop_esfera_escalon y se la pasamos al procedimiento ode45

function [value,isterminal,direction]=stop_esfera_escalon(t,x)
    value=[x(2), x(1)-pi/2];  %x(2) es velocidad, x(1) es posición
    isterminal=[1, 1];
    direction=[-1,1]; 
end

Cambiamos la velocidad inicial de la esfera v₀=3, y la integración de la ecuación diferencial se detiene cuando la posición angular es π/2. La variable xe nos proporciona la posición angular y la velocidad angular final

>> xe
xe =    1.5708    1.1643

Conservación de la energía

Durante el movimiento de rotacón alrededor de la esquina del escalón, la energía se conserva

${\displaystyle \begin{array}{l}\frac{1}{2}\left(\frac{7}{5}m{R}^2\right){\left(\frac{d\theta }{dt}\right)}^2+mg\sin \theta =\frac{1}{2}\left(\frac{7}{5}m{R}^2\right){\omega }_0^2+mg\sin {\theta }_0\\ {\left(\frac{d\theta }{dt}\right)}^2={\omega }_0^2-\frac{10}{7}\frac{g}{R}(\sin \theta -\sin {\theta }_0)\end{array}}$

Velocidad inicial crítica

Calculamos la velocidad angular mínima ω₀ para que la esfera justamente suba el escalón, es decir para que θ=π/2, dθ/dt=0.

${\displaystyle {\omega }_0^2=\frac{10}{7}\frac{g}{R}\left(1-\sin {\theta }_0\right)=\frac{10}{7}\frac{g}{R^2}h}$

La velocidad inicial crítica v_c con la que tenemos que lanzar la esfera por el plano horizontal para que justamente suba el escalón de altura h es

${\displaystyle v_c=\frac{R\sqrt{70gh}}{7R-5h}}$

• Si v₀<v_c entonces la esfera alcanzará el ángulo máximo θ_m<π/2 y retornará al plano horizontal con la misma velocidad v₀ pero de sentido contrario.



${\displaystyle \begin{array}{l}{\omega }_0^2=\frac{10}{7}\frac{g}{R}(\sin {\theta }_m-\sin {\theta }_0)\\ \sin {\theta }_m=\frac{7R}{10g}{\omega }_0^2+\frac{R-h}{R}\end{array}}$

• Si v₀>v_c la esfera subirá el escalón, θ=π/2, la velocidad de traslación de su centro será R(dθ/dt), con

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2={\omega }_0^2-\frac{10}{7}\frac{g}{R}(1-\sin {\theta }_0)\\ {\left(\frac{d\theta }{dt}\right)}^2={\omega }_0^2-\frac{10}{7}\frac{g}{R^2}h\end{array}}$

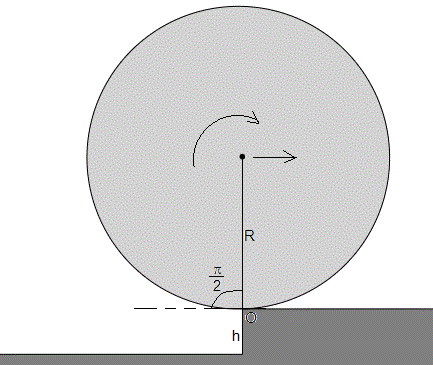
Movimiento sobre el escalón

La esfera rodará sin deslizar, la velocidad de traslación de su centro de masa será R(dθ/dt), y la velocidad angular de rotación alrededor de un eje que pasa por el centro de masas, dθ/dt.

Comprobamos que la energía cinética de la esfera después del impacto, E₂ se convierte en energía potencial mgh, en energía cinética de traslación del c.m. y en energía cinética de rotación alrededor de un eje que pasa por el c.m.

${\displaystyle \begin{array}{l}\frac{1}{2}\left(\frac{7}{5}m{R}^2\right){\omega }_0^2=mgh+\frac{1}{2}m{\left(R^2\frac{d\theta }{dt}\right)}^2+\frac{1}{2}\left(\frac{2}{5}m{R}^2\right){\left(\frac{d\theta }{dt}\right)}^2\\ \frac{7}{5}m{R}^2{\omega }_0^2=2mgh+\frac{7}{5}m{R}^2\left({\omega }_0^2-\frac{10}{7}\frac{g}{R^2}h\right)\\ \frac{7}{5}m{R}^2{\omega }_0^2=2mgh+\frac{7}{5}m{R}^2{\omega }_0^2-2mgh\end{array}}$

Ejemplos

• Radio de la esfera, R=1 m
• Altura del escalón, h=0.3 m

La velocidad inicial crítica v_c para que justamente la esfera suba el escalón, es

${\displaystyle v_c=\frac{R\sqrt{70gh}}{7R-5h}=\frac{1\sqrt{70·9.8·0.3}}{7·1-5·0.3}=2.608\text{m/s}}$

• Sea la velocidad de la esfera v₀=2 m/s menor que la crítica v_c

La velocidad angular inicial ω₀ después del choque con el escalón es

${\displaystyle {\omega }_0=\left(1-\frac{5}{7}\frac{h}{R}\right)\frac{v_0}{R}=\left(1-\frac{5}{7}\frac{0.3}{1}\right)\frac{2}{1}=1.57\text{rad/s}}$

El ángulo máximo θ_m que gira el centro de la esfera alrededor del eje que pasa por el punto O de impacto en el escalón, es

${\displaystyle \begin{array}{l}\sin {\theta }_m=\frac{7R}{10g}{\omega }_0^2+\frac{R-h}{R}\\ \sin {\theta }_m=\frac{7·1}{10·9.8}{1.57}^2+\frac{1-0.3}{1}\end{array}}$

θ_m=61.2°. La esfera regresa al plano horizontal con la misma velocidad v₀=2 m/s pero en sentido contrario

• Sea la velocidad de la esfera v₀=4 m/s mayor que la crítica v_c

${\displaystyle {\omega }_0=\left(1-\frac{5}{7}\frac{h}{R}\right)\frac{v_0}{R}=\left(1-\frac{5}{7}\frac{0.3}{1}\right)\frac{4}{1}=3.14\text{rad/s}}$

La velocidad de traslación del c.m. de la esfera, R(dθ/dt) cuando ha subido el escalón, es

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2={\omega }_0^2-\frac{10}{7}\frac{g}{R^2}h\\ R\frac{d\theta }{dt}=2.38\text{m/s}\end{array}}$

Actividades

Se ha fijado el radio de la esfera R=1 m. El dato de la masa m de la esfera no es necesario para este problema

Se introduce

• La altura h<R/2 del escalón en m, en el control titulado Altura escalón <0.5 m
• La velocidad de traslación del centro de la esfera v₀, sobre la plano horizontal, en el control titulado Velocidad de la esfera

Se pulsa el botón titulado Nuevo

Fuerzas en el punto de impacto en el escalón

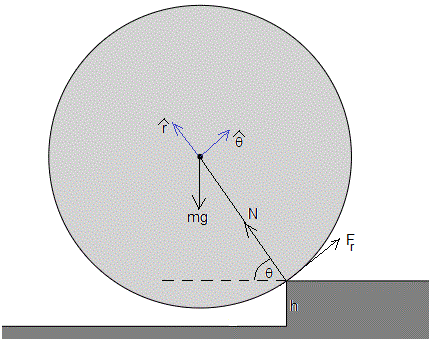
Las fuerzas que actúan sobre la esfera son:

• El peso, mg
• La fuerza que ejerce el punto de impacto sobre la esfera, la fuerza normal N
• La fuerza de rozamiento entre dicho punto y la esfera, F_r, tangente a la esfera en el punto de contacto

Para calcular la fuerza normal N y la fuerza de rozamiento F_r mientras la esfera gira alrededor de un eje que pasa por el punto de impacto en el escalón, adoptamos coordenadas polares.

En otras páginas hemos deducido la expresión del vector velocidad y el vector aceleración en coordenadas polares.

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\hfill \\ \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Teniendo en cuenta que r=R es constante, las ecuaciones del movimiento del c.m. en la dirección radial, $\widehat{r}$

${\displaystyle -mR{\left(\frac{d\theta }{dt}\right)}^2=N-mg\sin \theta }$

Esta es la ecuación de la dinámica del movimiento circular del c.m. de la esfera que describe un arco de circunferencia de radio R

Conocido el cuadrado del la velocidad angular de rotación (conservación de la energía), despejamos la fuerza normal N

${\displaystyle \begin{array}{l}-mR\left\{{\omega }_0^2-\frac{10}{7}\frac{g}{R}(\sin \theta -\sin {\theta }_0)\right\}=N-mg\sin \theta \hfill \\ N=\frac{17}{7}mg\sin \theta -mR{\omega }_0^2-\frac{10}{7}mg\sin {\theta }_0\hfill \end{array}}$

La ecuación del movimiento en la dirección $\widehat{\theta }$

${\displaystyle mR\frac{d^2\theta }{d{t}^2}=F_r-mg\cos \theta }$

La ecuación de la dinámica de rotación alrededor de un eje que pasa por el c.m. es

${\displaystyle \left(\frac{2}{5}m{R}^2\right)\frac{d^2\theta }{d{t}^2}=-F_{r}R}$

Combinado estas dos últimas ecuaciones, obtenemos

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{5}{7}\frac{g}{R}\cos \theta }$

Que es la ecuación de la dinámica de rotación alrededor de un eje que pasa por el punto de impacto en el escalón, que hemos deducido en apartados anteriores. Conocida la aceleración angular, la fuerza de rozamiento vale

${\displaystyle F_r=\frac{2}{7}mg\cos \theta }$

en el sentido indicado en la figura.

Supondremos en este problema que la fuerza de rozamiento F_r se mantiene siempre inferior a su máximo valor μN, por tanto, la esfera no desliza sobre el punto de impacto O en el escalón

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1202, pp. 327-328