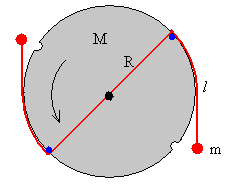
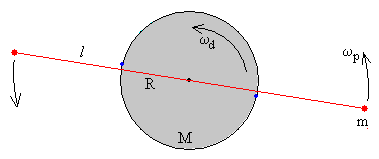
Consideremos un disco de masa M y de radio R, que gira alrededor de un eje que pasa por su centro. Dos partículas iguales de masa m, están sujetas en los extremos de uno de sus diámetros. Se pone el disco en rotación, a continuación se liberan las partículas de su sujeción pero permanecen unidas al eje del disco mediante dos hilos inextensibles de longitud (l+R) tal como se muestra en la figura.

Choques frontales elásticos

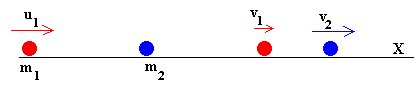
Sea un choque frontal elástico entre dos partículas, estando inicialmente en reposo la segunda u₂=0

1. Sea aplica el principio de conservación del momento lineal

m₁u₁ =m₁v₁+m₂v₂

2. La energía cinética inicial es igual a la final

${\displaystyle \frac{1}{2}{m}_1{u}_1^2=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2}$

Dadas las velocidades u₁ y u₂ de las partículas m₁ y m₂ antes del choque, calculamos las velocidades de las partículas v₁ y v₂ después del choque, resolviendo este sistema de dos ecuaciones con dos incógnitas.

${\displaystyle v_1=\frac{m_1-m_2}{m_1+m_2}{u}_1{v}_2=\frac{2m_1{u}_1}{m_1+m_2}}$

Después del choque, la primera partícula:

• Puede permanecer en reposo, si m₁=m₂

• Llevar el mismo sentido de la velocidad inicial, si m₁>m₂

• Cambiar el sentido de la velocidad inicial, si m₁<m₂

La situación inicial y final del sistema

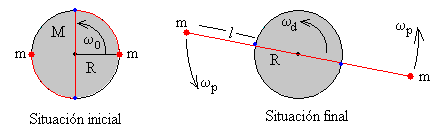
A medida que las partículas describen un movimiento en espiral hacia fuera, la velocidad angular de rotación del disco disminuye, hasta que finalmente:

• Alcanza una velocidad angular constante en el mismo sentido

• Se detiene

• Invierte el sentido de la velocidad angular final constante.

Las dos partículas se mueven en el sentido inicial en una trayectoria circular de radio (R+l).

En este apartado, vamos a comparar la situación inicial y la final y luego, analizaremos la evolución desde el estado inicial al final

Situación inicial

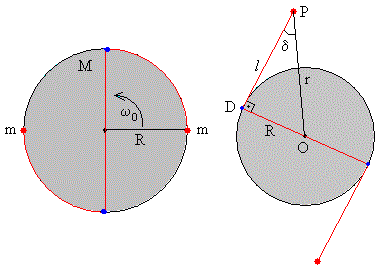
Las dos partículas de masa m están sujetas al borde del disco de masa M y radio R. Sea ω₀ la velocidad angular inicial de rotación alrededor del eje que pasa por el centro del disco

• El momento angular L del sistema es

${\displaystyle L=\left(\frac{1}{2}M{R}^2\right){\omega }_0+2·m{R}^2{\omega }_0}$

• La energía E del sistema es

${\displaystyle E=\frac{1}{2}\left(\frac{1}{2}M{R}^2\right){\omega }_0^2+2·\frac{1}{2}m{R}^2{\omega }_0^2}$

Situación final

El disco gira con velocidad angular ω_d, y las dos partículas describen una trayectoria circular de radio l+R, con velocidad angular ω_p.

• El momento angular L del sistema es

${\displaystyle L=\left(\frac{1}{2}M{R}^2\right){\omega }_d+2·m{(R+l)}^2{\omega }_p}$

• La energía E del sistema es

${\displaystyle E=\frac{1}{2}\left(\frac{1}{2}M{R}^2\right){\omega }_d^2+2·\frac{1}{2}m{(R+l)}^2{\omega }_p^2}$

Las fuerzas exteriores actúan en el eje del disco. El sistema no es aislado, pero el momento de las fuerzas exteriores respecto del eje de rotación es cero. El momento angular respecto del eje de rotación permanece constante.

${\displaystyle \overrightarrow{M_{ext}}=\frac{d\overrightarrow{L}}{dt}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

Como no hay trabajo de las fuerza interiores (se supone que la cuerda que une las partículas es inextensible y está tensa en todo momento), la energía inicial es igual a la final.

Tenemos un sistema de dos ecuaciones con dos incógnitas similar al que describe un choque frontal elástico.

${\displaystyle \begin{array}{l}c{\omega }_0=a{\omega }_d+b{\omega }_{p}a=\frac{1}{2}M{R}^{2}b=2m{\left(R+l\right)}^2\\ c{\omega }_0^2=a{\omega }_d^2+b{\omega }_p^{2}c=\frac{1}{2}M{R}^2+2m{R}^2\end{array}}$

La solución de este sistema de dos ecuaciones es

${\displaystyle {\omega }_d=\frac{ca-\sqrt{abc(a+b-c)}}{a(a+b)}{\omega }_0{\omega }_p=\frac{cb+\sqrt{abc(a+b-c)}}{b(a+b)}{\omega }_0}$

• la velocidad angular de las partículas ω_p es siempre positiva.

• la velocidad angular del disco ω_d puede ser positiva, negativa o nula,

Estudiamos este último caso: ω_d es nula cuando c²a²=abc(a+b-c), despejamos b de la ecuación de segundo grado

b²-b(c-a)-ca=0

La solución positiva es b=c, o bien

${\displaystyle \frac{4m}{M}=\frac{R^2}{{(R+l)}^2-R^2}}$

Esta es la relación entre las magnitudes que describen el sistema, para que el disco se detenga ω_d=0 en la situación final.

• Masa m de cada una de las partículas

• Masa del disco M

• Radio del disco R

• Longitud de la cuerda (R+l) que une cada partícula al eje del disco

Evolución desde el estado inicial al final

En la figura, se muestra las distintas etapas del movimiento, desde la situación inicial a la final, que iremos analizando a lo largo de este apartado.

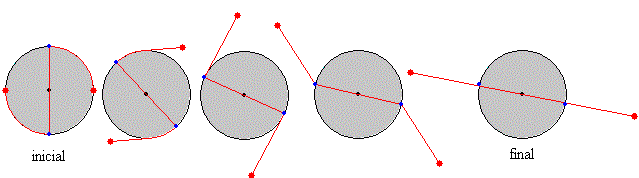
La fuerza centrífuga hace que las partículas, una vez liberadas de su sujeción en el borde del disco, describan un movimiento en forma de espiral.

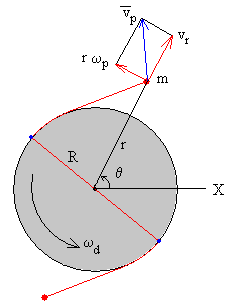
Analizamos el sistema en el instante t en el que una de las partículas está en la posición dada por la distancia radial r, y por el ángulo θ que hace con el eje X (coordenadas polares). La otra partícula está en la posición opuesta tal como se aprecia en la figura.

Descomponemos el vector velocidad de la partícula $\overrightarrow{v_p}$ en la dirección radial v_r y en la dirección tangencial v_θ=r·ω_p. Donde v_r=dr/dt y v_θ=r·dθ/dt. Supongamos que la velocidad angular del disco en este instante es ω_d.

• El momento angular se expresa para esta situación

${\displaystyle L=\left(\frac{1}{2}M{R}^2\right){\omega }_d+2·m{r}^2{\omega }_p}$     (1)

• La energía del sistema es

${\displaystyle E=\frac{1}{2}\left(\frac{1}{2}M{R}^2\right){\omega }_d^2+2·\frac{1}{2}m{v}_p^2=\frac{1}{2}\left(\frac{1}{2}M{R}^2\right){\omega }_d^2+2·\frac{1}{2}m\left(v_r^2+r^2{\omega }_p^2\right)}$        (2)

Primera etapa del movimiento

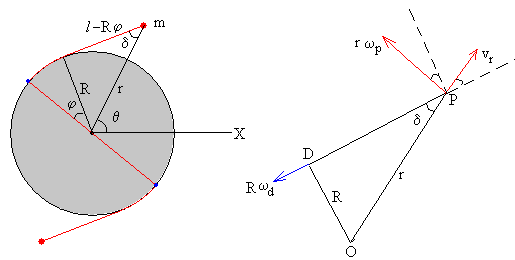
El punto D del borde del disco y la partícula situada en P están unidos por una porción de cuerda inextensible. Sabiendo que la velocidad del punto D del borde del disco es R·ω_d, relacionamos la velocidad angular del disco ω_d con las componentes de la velocidad $\overrightarrow{v_p}$ de la partícula. Para ello, proyectamos las velocidades del punto P y del punto D a lo largo de la recta que une el punto P y D

R·ω_d=r·ω_p·sinδ-v_r·cosδ,   (3)

donde sinδ=R/r

Tenemos tres ecuaciones con tres incógnitas:

• las componentes radial v_r=dr/dt, y tangencial v_θ=r·ω_p=r·dθ/dt de la velocidad de cada partícula

• la velocidad angular de rotación del disco ω_d.

Se despeja ω_p y ω_d de la primera y tercera ecuación, en función de r y v_r

${\displaystyle {\omega }_p=\frac{d\theta }{dt}=\frac{2L+MR·v_r·\cos \delta }{r(4mr+MR\text{sin}\delta )}{\omega }_d=\frac{2L\text{sin}\delta -4mr·v_r·\cos \delta }{R(4mr+MR\text{sin}\delta )}}$

Se introduce las expresiones de ω_p y de ω_d en la segunda ecuación, y después de un intenso trabajo realizando operaciones algebraicas, despejamos v_r.

${\displaystyle v_r=\frac{dr}{dt}=\sqrt{\frac{2E(4m{r}^2+M{R}^2)-2L^2}{2m{r}^2(M+4m)}}}$

Para calcular la posición (r, θ) de las partículas, se resuelve el sistema de dos ecuaciones diferenciales de primer orden mediante procedimientos numéricos

${\displaystyle \frac{dr}{dt}=f(r)\frac{d\theta }{dt}=g(r)}$

Como vemos en la parte derecha de la figura, la posición angular del diámetro del disco está relacionada con la posición angular de la partícula (se ha tomado l=πR/2, pero puede generalizarse para cualquier l).

θ+(π/2-δ)+φ.

En el triángulo rectángulo que forma la posición P de la partícula, el punto D de contacto de la cuerda con el disco y el centro O del disco (véase de la parte izquierda de la figura)

${\displaystyle \tan \delta =\frac{R}{l-R\phi }\phi =\frac{l}{R}-\frac{1}{\tan \delta }\text{sin}\delta =\frac{R}{r}}$

Situación inicial

En el instante inicial t=0, la partícula se encuentra en θ=0, y r=R. Con estas condiciones iniciales v_r=0, por lo que lo procedimiento numérico no progresa. En la simulación, se toma como condiciones iniciales t=0, θ=0, y r=R+ΔR, siendo ΔR una cantidad pequeña, una milésima del valor de R.

Situación final

La cuerda se acaba de desenrollar del disco cuando la partícula dista del origen r²=R²+l² o bien, cuando el ángulo δ, vale tanδ=R/l, o cuando φ=0.

Segunda etapa del movimiento

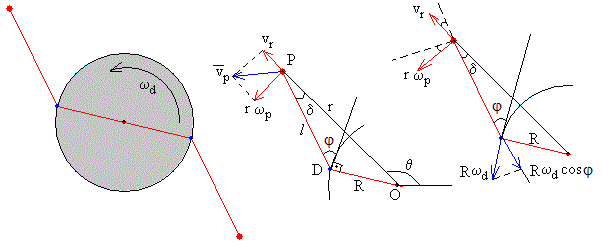
El punto D del borde del disco y la partícula situada en P están unidos por una porción de hilo inextensible. Sabiendo que la velocidad del punto D del borde del disco es R·ω_d, relacionamos la velocidad angular del disco ω_d con las componentes de la velocidad $\overrightarrow{v_p}$ de la partícula. Para ello, proyectamos las velocidades del punto P y del punto D a lo largo de la recta que une el punto P y D.

R·ω_d·cosφ=r·ω_p·sinδ-v_r·cosδ,   (3)

El ángulo φ es el que forma el hilo con la tangente al disco en el punto de contacto D.

Aplicando el teorema del seno y del coseno al triángulo POD, tenemos que

${\displaystyle \begin{array}{l}\cos \phi =\frac{r}{R}\text{sin}\delta \\ R^2=r^2+l^2-2rl\cos \delta \end{array}}$

Tenemos de nuevo tres ecuaciones con tres incógnitas, de las cuales las dos primeras no cambian ya que expresan la constancia del momento angular y de la energía cinética. Las incógnitas son, de nuevo,

• Las componentes radial v_r=dr/dt, y tangencial v_θ=r·ω_p=r·dθ/dt de la velocidad de cada partícula

• La velocidad angular de rotación del disco ω_d.

Se despeja ω_p y ω_d de la primera y tercera ecuación, en función de r y v_r

${\displaystyle {\omega }_p=\frac{d\theta }{dt}=\frac{2rL\text{sin}\delta +M{R}^2·v_r·\cos \delta }{r(4m{r}^2+M{R}^2)\text{sin}\delta }{\omega }_d=\frac{2L\text{sin}\delta -4mr·v_r\cos \delta }{(4m{r}^2+M{R}^2)\text{sin}\delta }}$

Se introduce las expresiones de ω_p y de ω_d en la segunda ecuación, y después de un intenso trabajo realizando operaciones algebraicas, despejamos v_r.

${\displaystyle v_r=\frac{dr}{dt}=\sqrt{\frac{E(4m{r}^2+M{R}^2)-L^2}{(4m^2{r}^2+mM{R}^2/{\text{sin}}^2\delta )}}}$

Para calcular la posición (r, θ) de la partícula se resuelve el sistema de dos ecuaciones diferenciales de primer orden mediante procedimientos numéricos

${\displaystyle \frac{dr}{dt}=f(r)\frac{d\theta }{dt}=g(r)}$

La posición angular del diámetro del disco, como vemos en la figura es

θ+π-(π/2+φ+δ)= θ+π/2-φ-δ

con

${\displaystyle \cos \delta =\frac{r^2+l^2-R^2}{2rl}\cos \phi =\frac{r}{R}\text{sin}\delta }$

Tercera etapa del movimiento

Situación inicial

La situación inicial de la segunda etapa del movimiento, es la situación final de la primera etapa. En el instante t=t₀, la distancia de la partícula al origen es r²=R²+l², y forma un ángulo θ₀ con el eje X.

Situación final

Se produce cuando la cuerda adopta la forma de un segmento de recta que pasando por el centro del disco une las dos partículas. Los enganches situados en la periferia del disco (en color azul en la simulación) dejan de actuar y el disco se mueve con una velocidad angular ω_d final constante y las partículas se mueven en una trayectoria circular de radio (R+l) con velocidad angular final constante ω_p.

Ejemplos

• La masa de cada una de las partículas m=0.07 kg

• La masa del disco M=1.0 kg

• El radio del disco R=0.5 m

• La longitud de la cuerda (R+l)=R+πR/2, de modo que l=0.785 m

• La velocidad angular inicial del sistema ω₀=1 rad/s

El momento angular es

${\displaystyle L=\left(\frac{1}{2}1.0·{0.5}^2\right)1.0+2·0.07·{0.5}^2·1.0=0.16{\text{kgm}}^{\text{2}}\text{/s}}$

La energía E del sistema es

${\displaystyle E=\frac{1}{2}\left(\frac{1}{2}1.0·{0.5}^2\right){1.0}^2+2·\frac{1}{2}0.07·{0.5}^2{1.0}^2=0.08\text{J}}$

En la situación final, el disco gira con velocidad angular ω_d, y las dos partículas describen una trayectoria circular de radio l+R=1.285 m, con velocidad angular ω_p.

Planteamos las ecuaciones de constancia del momento angular y de la energía

${\displaystyle \begin{array}{l}0.16=\frac{1}{2}1.0·{0.5}^2·{\omega }_d+2·0.07·{1.285}^2·{\omega }_p\\ 0.08=\frac{1}{2}\left(\frac{1}{2}1.0·{0.5}^2\right)·{\omega }_d^2+2·\frac{1}{2}0.07·{1.285}^2·{\omega }_p^2\end{array}}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas

ω_d=-0.227 rad/s y ω_p=0.815 rad/s

Ejemplo 2:

La masa crítica de las partículas para la cual, el disco se detiene se obtiene de la relación

${\displaystyle \frac{4m}{M}=\frac{R^2}{{(R+l)}^2-R^2}\frac{4m}{1.0}=\frac{{0.5}^2}{{1.285}^2-{0.5}^2}m=0.0446\text{kg}}$

Comprobación. Para este valor de la masa m de cada una de las partículas

El momento angular del sistema será

L=0.1473 kgm²/s

La energía del sistema será

E=0.0736 J

Planteamos el sistema de dos ecuaciones con dos incógnitas para calcular la velocidad angular del disco ω_d, y la velocidad angular de las partículas ω_p.

${\displaystyle \begin{array}{l}0.1473=0.125·{\omega }_d+0.1473·{\omega }_p\\ 0.1473=0.125·{\omega }_d^2+0.1473·{\omega }_p^2\end{array}}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas

ω_d=0.0 rad/s y ω_p=1.0 rad/s

Se sugiere al lector que compruebe que cuando m=M/π=1.0/π=0.3183 kg, el disco invierte el sentido de su velocidad inicial de 1 rad/s.

Actividades

Se introduce

• La masa m de la partícula en kg, en el control titulado Masa partícula.

• La masa del disco se ha fijado en el valor M=1.0 kg

• El radio del disco se ha fijado en el valor R=0.5 m

• La longitud de la cuerda (R+l) que une el centro del disco y cada partícula se ha fijado en el valor (R+πR/2) por lo que l= πR/2=0.785 m

• La velocidad angular inicial del sistema formado por el disco y las partículas se ha fijado en el valor ω₀=1 rad/s.

Se pulsa el botón titulado Nuevo.

Observamos el movimiento del disco y de las partículas desde la situación inicial a la situación final. En la parte izquierda, se representa mediante un diagrama de barras la energía cinética y el momento angular del disco (en color azul), y de las dos partículas (en color rojo). El momento angular total permanece constante y también la energía. Se va transfiriendo energía y momento angular del disco hacia las partículas y eventualmente de las partículas al disco cuando éste invierte el sentido de  su movimiento.

En la parte derecha, se proporcionan los datos referentes a la velocidad angular de las partículas y del disco, del momento angular y de la energía del sistema formado por el disco y las partículas.

Referencias

Mungan C. The satellite derotator. The Physics Teacher, vol 40, September 2002, pp. 368-372

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017