Transferencia de la velocidad en un choque por medio de una varilla interpuesta (II)

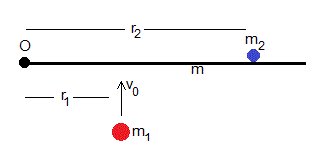
Sea una varilla de masa m y longitud l, que puede girar alrededor de un eje perpendicular a la varilla y que pasa por su extremo O. Una partícula de masa m₁ lleva una velocidad inicial v₀ y que dista r₁ de O choca con la varilla, inicialmente en reposo

La varilla a su vez, choca con otra partícula inicialmente en reposo, de masa m₂ que dista r₂ del eje de rotación

Los choques de la partícula de masa m₁ con la varilla y de la varilla con la partícula de masa m₂ se consideran en una primera aproximación al problema, elásticos

Se pide calcular las velocidades finales (inmediatamente después del choque) v₁ y v₂ de las partículas y la velocidad angular ω de rotación de la varilla.

Para resolver el problema aplicamos

Conservación del momento angular
Balance energético. Conservación de la energía cinética en el caso de choques elásticos

El momento lineal no se conserva ya que no es un sistema aislado, la varilla está sujeta en el eje O

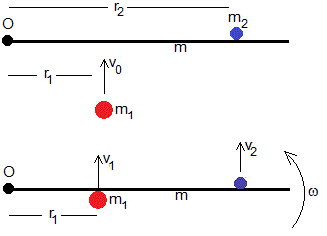
Comparando la situación inicial y final, en este problema tenemos dos ecuaciones pero tres incógnitas:

la velocidad v₁ de la partícula de masa m₁ después del choque
la velocidad v₂ de la partícula de masa m₂ después del choque
La velocidad angular ω de la varilla

Pero solamente disponemos de dos ecuaciones, estamos en un problema similar a la estática de una escalera apoyada en paredes perpendiculares

Para resolver el problema, supondremos que se producen dos choques consecutivos:

de la partícula de masa m₁ con la varilla
de la varilla con la partícula de masa m₂

Aplicando el teorema de Steiner, calculamos el momento de inercia de la varilla respecto de un eje perpendicular que pasa por su extremo O

$I_{O} = \frac{1}{12} m l^{2} + m {(\frac{l}{2})}^{2} = \frac{1}{3} m l^{2}$

Choques elásticos

Primer choque

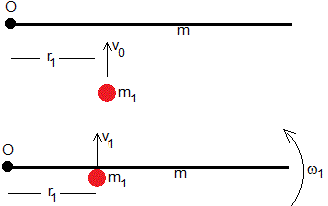
Conservación del momento angular

El momento angular inicial (respecto de O) es

$L_{O} = m_{1} r_{1} v_{0}$

El momento angular después del choque es

$L_{O} = I_{O} ω_{1} + m_{1} r_{1} v_{1} = \frac{1}{3} m l^{2} ω_{1} + m_{1} r_{1} v_{1}$

Despejamos la velocidad angular de rotación de la varilla

$\begin{array}{l} m_{1} r_{1} v_{0} = \frac{1}{3} m l^{2} ω_{1} + m_{1} r_{1} v_{1} \\ ω_{1} = \frac{3 m_{1} r_{1}}{m l^{2}} (v_{0} - v_{1}) \end{array}$

Conservación de la energía cinética

La energía cinética inicial es

$E_{0} = \frac{1}{2} m_{1} v_{0}^{2}$

La energía cinética después del choque es

$E_{0} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} (\frac{1}{3} m l^{2}) ω_{1}^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} (\frac{1}{3} m l^{2}) \frac{9 m_{1}^{2} r_{1}^{2}}{m^{2} l^{4}} {(v_{0} - v_{1})}^{2}$

La conservación de la energía conduce a una ecuación de segundo grado en v₁

$\begin{array}{l} \frac{1}{2} m_{1} v_{0}^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} (\frac{1}{3} m l^{2}) \frac{9 m_{1}^{2} r_{1}^{2}}{m^{2} l^{4}} {(v_{0} - v_{1})}^{2} \\ m_{1} (3 m_{1} r_{1}^{2} + m l^{2}) v_{1}^{2} - 6 m_{1}^{2} r_{1}^{2} v_{0} v_{1} + m_{1} (3 m_{1} r_{1}^{2} - m l^{2}) v_{0}^{2} = 0 \end{array}$

cuya solución es

$\begin{array}{l} m_{1} (3 m_{1} r_{1}^{2} + m l^{2}) v_{1}^{2} - 6 m_{1}^{2} r_{1}^{2} v_{0} v_{1} + m_{1} (3 m_{1} r_{1}^{2} - m l^{2}) v_{0}^{2} = 0 \\ v_{1} = \frac{6 m_{1}^{2} r_{1}^{2} v_{0} \pm \sqrt{36 m_{1}^{4} r_{1}^{4} v_{0}^{2} - 4 m_{1}^{2} (3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{1} r_{1}^{2} - m l^{2}) v_{0}^{2}}}{2 m_{1} (3 m_{1} r_{1}^{2} + m l^{2})} \\ v_{1} = \frac{3 m_{1} r_{1}^{2} \pm m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} \end{array}$

La primera solución corresponde a la identidad v₁=v₀. La solución es

$\begin{array}{l} v_{1} = \frac{3 m_{1} r_{1}^{2} - m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} \\ ω_{1} = \frac{3 m_{1} r_{1}}{m l^{2}} (v_{0} - v_{1}) = \frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} \end{array}$

Segundo choque

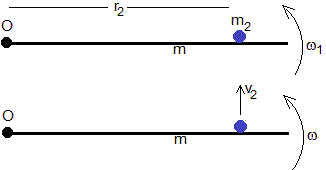
Conservación del momento angular

El momento angular inicial (respecto de O) es

$L_{1} = (\frac{1}{3} m l^{2}) ω_{1} = \frac{2 m_{1} r_{1} \cdot m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0}$

El momento angular después del choque es

$L_{1} = I_{0} ω + m_{2} r_{2} v_{2} = (\frac{1}{3} m l^{2}) ω + m_{2} r_{2} v_{2}$

Despejamos la velocidad angular de rotación de la varilla

$\begin{array}{l} \frac{2 m_{1} r_{1} \cdot m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} = (\frac{1}{3} m l^{2}) ω + m_{2} r_{2} v_{2} \\ ω = \frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} - \frac{3 m_{2} r_{2}}{m l^{2}} v_{2} \end{array}$

Conservación de la energía cinética

La energía cinética inicial es

$E_{1} = \frac{1}{2} I_{0} ω_{1}^{2} = \frac{1}{2} (\frac{1}{3} m l^{2}) {(\frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0})}^{2} = \frac{6 m_{1}^{2} r_{1}^{2} \cdot m l^{2}}{{(3 m_{1} r_{1}^{2} + m l^{2})}^{2}} v_{0}^{2}$

La energía cinética después del choque es

$E_{1} = \frac{1}{2} I_{0} ω^{2} + \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} (\frac{1}{3} m l^{2}) {(\frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} - \frac{3 m_{2} r_{2}}{m l^{2}} v_{2})}^{2} + \frac{1}{2} m_{2} v_{2}^{2}$

La conservación de la energía conduce a una ecuación de segundo grado en v₂

$\frac{1}{2} m_{2} (\frac{3 m_{2} r_{2}^{2}}{m l^{2}} + 1) v_{2}^{2} - \frac{6 m_{1} r_{1} \cdot m_{2} r_{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} v_{2} = 0$

La solución v₂=0 es la identidad, luego

$\begin{array}{l} v_{2} = \frac{12 m_{1} r_{1} \cdot r_{2} \cdot m l^{2}}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0} \\ ω = \frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} - \frac{3 m_{2} r_{2}}{m l^{2}} v_{2} = \frac{6 m_{1} r_{1} (- 3 m_{2} r_{2}^{2} + m l^{2})}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0} \end{array}$

La velocidad angular de rotación después del choque, ω=0 si

$m_{2} r_{2}^{2} = \frac{1}{3} m l^{2}$

El segundo miembro es el momento de inercia de la varilla

El análisis estará completo siempre que la varilla después del segundo choque no vuelva a chocar con la primera partícula de masa m₁ y velocidad v₁. No sucederá si ωr₁>v₁

$\begin{array}{l} ω r_{1} > v_{1} \\ \frac{6 m_{1} r_{1}^{2} (- 3 m_{2} r_{2}^{2} + m l^{2})}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0} > \frac{3 m_{1} r_{1}^{2} - m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} \\ 6 m_{1} r_{1}^{2} (- 3 m_{2} r_{2}^{2} + m l^{2}) > (3 m_{1} r_{1}^{2} - m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2}) \\ m l^{2} (3 m_{1} r_{1}^{2} + 3 m_{2} r_{2}^{2} + m l^{2}) > 27 m_{1} r_{1}^{2} \cdot m_{2} r_{2}^{2} \end{array}$

La energía cinética no se conserva

Volvemos a resolver el problema, sustituyendo la ecuación de la conservación de la energía, por el balance energético en términos del coeficiente de restitución e

$v_{1} - v_{2} = - e (u_{1} - u_{2})$

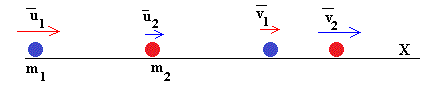
Supondremos que existen dos coeficientes de restitución:

e₁ para describir el choque de la partícula de masa m₁ con la varilla (primer choque)
e₂ para describir el choque de la varilla con partícula de masa m₂ (segundo choque)

Primer choque

Conservación del momento angular

$\begin{array}{l} m_{1} r_{1} v_{0} = \frac{1}{3} m l^{2} ω_{1} + m_{1} r_{1} v_{1} \\ ω_{1} = \frac{3 m_{1} r_{1}}{m l^{2}} (v_{0} - v_{1}) \end{array}$

Balance energético

$v_{1} - r_{1} ω_{1} = - e_{1} v_{0}$

Despejamos la velocidad angular ω₁ de la varilla y la velocidad final v₁ de la partícula de masa m₁, en el sistema de dos ecuaciones

$\begin{array}{l} ω_{1} = (1 + e_{1}) \frac{3 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} \\ v_{1} = \frac{3 m_{1} r_{1}^{2} - e_{1} m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} \end{array}$

Segundo choque

Conservación del momento angular

$\begin{array}{l} (\frac{1}{3} m l^{2}) ω_{1} = (\frac{1}{3} m l^{2}) ω + m_{2} r_{2} v_{2} \\ ω = \frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0} - \frac{3 m_{2} r_{2}}{m l^{2}} v_{2} \end{array}$

Balance energético

$ω r_{2} - v_{2} = - e_{2} ω_{1} r_{2}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas: la velocidad final de rotación de la varilla ω y la velocidad final v₂ de la partícula de masa m₂

$\begin{array}{l} v_{2} = \frac{3 m_{1} r_{1} r_{2} \cdot m l^{2} (e_{2} + e_{1} e_{2} + 2)}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0} \\ ω = \frac{3 m_{1} r (2 m l^{2} - 3 m_{2} r_{2}^{2} (1 + e_{1}) e_{2})}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0} \end{array}$

Choques elásticos

Para los choque elástico, e₁=e₂=1

Comprobamos que se obtienen las expresiones del apartado titulado 'Choques elásticos'

Primer choque

$ω_{1} = \frac{6 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0}, v_{1} = \frac{3 m_{1} r_{1}^{2} - m l^{2}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0}$

Segundo choque

$v_{2} = \frac{12 m_{1} r_{1} r_{2} \cdot m l^{2}}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0}, ω = \frac{6 m_{1} r_{1} (m l^{2} - 3 m_{2} r_{2}^{2})}{(3 m_{1} r_{1}^{2} + m l^{2}) (3 m_{2} r_{2}^{2} + m l^{2})} v_{0}$

Choques completamente inelásticos

Para resolver los choques completamente inelásticos no vale con poner e₁=e₂=0, en las fórmulas generales. Es preciso volver a describir los dos choques consecutivos

Primer choque

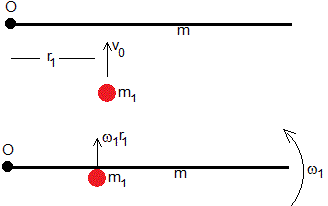
Conservación del momento angular

$\begin{array}{l} m_{1} r_{1} v_{0} = \frac{1}{3} m l^{2} ω_{1} + m_{1} r_{1} v_{1} \\ ω_{1} = \frac{3 m_{1} r_{1}}{m l^{2}} (v_{0} - v_{1}) \end{array}$

Balance energético

$v_{1} - r_{1} ω_{1} = 0$

Despejamos la velocidad angular ω₁ de la varilla después del choque. La velocidad de la partícula de masa m₁ es v₁=ω₁r₁

$ω_{1} = \frac{3 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + m l^{2}} v_{0}$

Segundo choque

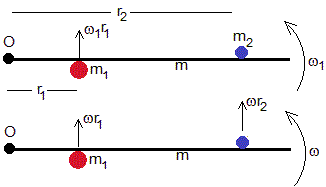
Conservación del momento angular

$(\frac{1}{3} m l^{2} + m_{1} r_{1}^{2}) ω_{1} = (\frac{1}{3} m l^{2} + m_{1} r_{1}^{2}) ω + m_{2} r_{2} v_{2}$

Balance energético

$ω r_{2} - v_{2} = 0$

Despejamos la velocidad angular ω de la varilla después del choque. La velocidad de la partícula de masa m₂ es v₂=ω₂r₁

$ω = \frac{3 m_{1} r_{1}}{3 m_{1} r_{1}^{2} + 3 m_{2} r_{2}^{2} + m l^{2}} v_{0}$

Referencias

Kirk T. McDonald. An Ill-Posed Problem in Rigid-Body Dynamics. June 11, 2011