Movimiento sobre la cúpula semiesférica
con rozamiento
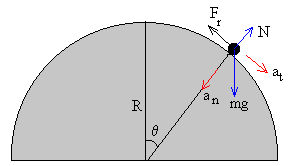
Dibujamos las fuerzas que actúan sobre la partícula, cuando se ha desplazado un ángulo θ.
- El peso mg
- La reacción N de la cúpula
- La fuerza de rozamiento Fr=μN
La partícula describe un movimiento circular con aceleración tangencial at y aceleración normal an. Estas aceleraciones se determinan aplicando la segunda ley de Newton
-
Ecuación del movimiento en la dirección tangencial
Ecuación del movimiento en la dirección normal
mg·sinθ-Fr=mat
mg·cosθ-N=man
Combinando estas dos ecuaciones obtenemos la ecuación diferencial del movimiento
que se resuelve por procedimientos numéricos con las siguientes condiciones iniciales t=0, θ=0, dθ/dt=v0/R. Donde v0 es la velocidad inicial. En un apartado más abajo, resolveremos utilizando MATLAB la ecuación del movimiento. En la simulación se utiliza el procedimiento de Runge-Kutta
La partícula se detiene o deja de estar contacto con la cúpula
Las aceleraciones tangencial y normal se expresan en función de la velocidad v del siguiente modo
Despejando la reacción N en la segunda ecuación del movimiento y sustituyéndola en la primera, obtenemos la ecuación diferencial de primer orden
Llamando nos queda la ecuación diferencial
La solución de la ecuación diferencial se compone de dos términos:
La solución particular x1=Asinθ+Bcosθ
Introduciendo la solución particular en la ecuación diferencial obtenemos los valores de los coeficientes A y B
Buscamos la solución de la ecuación diferencial homogénea
Integrando ambos miembros obtenemos lnx=2μθ+cte, o bien, x2=C·exp(2μθ)
La solución completa es x=x1+x2
La constante C se determina a partir de las condiciones iniciales, para θ=0, v=v0
Finalmente, la ecuación que nos proporciona la velocidad v en función del ángulo θ, es
-
Si no hay rozamiento, μ=0
Si hay rozamiento μ≠0, pueden ocurrir dos casos:
- Que la partícula deje de estar en contacto con la cúpula, es decir, la reacción N se haga cero, con v>0
- Que la partícula se detenga v=0, con N>0
La misma expresión se obtiene aplicando el principio de conservación de la energía.
La partícula, deja de tener contacto con la cúpula para el ángulo θs tal que N=0.
Obtenemos este ángulo en la ecuación del movimiento en la dirección radial
Una vez alcanzada la posición θs, la partícula describe un movimiento parabólico tal como ha sido descrito en el apartado anterior.
Sea una cúpula semiesférica de radio R=1, la velocidad inicial en la posición θ=0, es v0=2 m/s, el coeficiente de rozamiento es μ=0.4. Representamos v2/(Rg) y la reacción N/mg en función del ángulo θ
R=1; %radio
mu=0.4; %coeficiente de rozamiento
v0=2; %velocidad inicial para theta=0,
v2=@(x) v0^2*exp(2*mu*x*pi/180)/(R*9.8)+((4*mu^2-2)*
(cos(x*pi/180)-exp(2*mu*x*pi/180))-6*mu*sin(x*pi/180))/(4*mu^2+1);
N=@(x) cos(x*pi/180)-v2(x);
subplot(2,1,1)
fplot(v2,[0,pi/2]*180/pi)
grid on
ylim([0,1.5])
xlabel('\theta')
ylabel('v^2/Rg')
title('Velocidad')
subplot(2,1,2)
fplot(N,[0,pi/2]*180/pi)
grid on
ylim([-1,1])
xlabel('\theta')
ylabel('N/mg')
title('Normal')
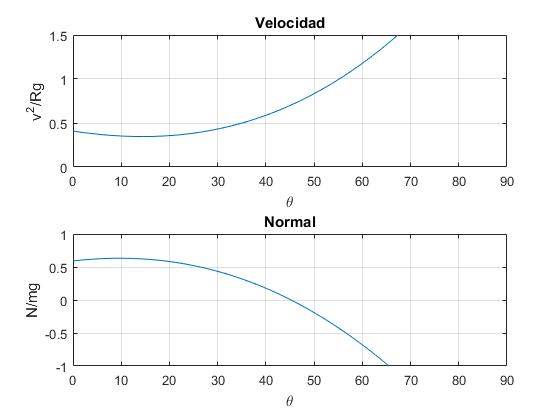
La partícula no se detiene. Para el ángulo cercano a 45° la reacción N se hace cero. Calculamos este ángulo con la función fzero de MATLAB
>> fzero(N,[0,pi/2]*180/pi) ans = 45.2367
Cambiamos el coeficiente de rozamiento μ=1
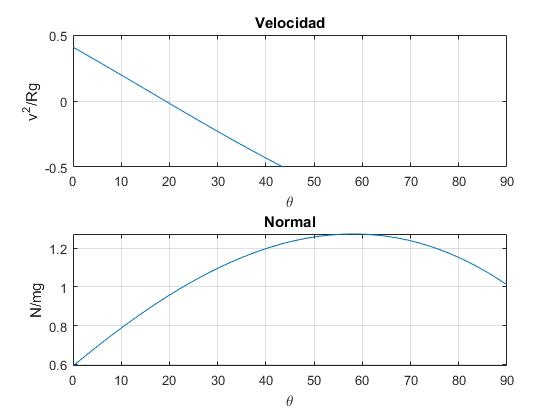
Observamos que la reacción del plano N no se hace nula, sin embargo, la velocidad se hace nula para un ángulo próximo a 20° que calculamos con la función fzero de MATLAB
>> fzero(v2,[0,pi/2]*180/pi) ans = 19.1566
Velocidad inicial crítica y ángulo crítico
Fijamos el coeficiente de rozamiento, por ejemplo, μ=1, y vamos cambiando la velocidad inicial v0 con el que lanzamos la partícula en la posición θ=0.
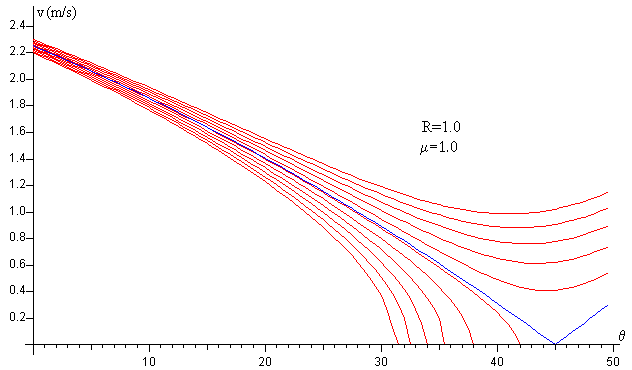
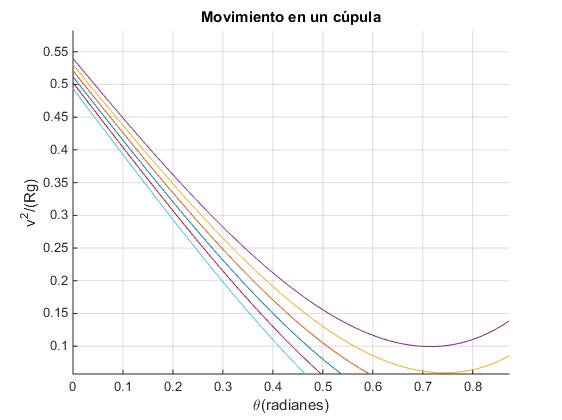
En la figura, se representa (en color rojo) la velocidad de la partícula v en función del ángulo θ, para varias velocidad iniciales v0=2.2, 2.21, 2.22… 2.29 m/s. En color azul, se representa la velocidad de la partícula v en función del ángulo θ para la velocidad inicial v0=2.2522046 m/s. Se ha fijado el radio de la cúpula R=1.0 m y el coeficiente de rozamiento, μ=1.
- La partícula se detiene para un ángulo θs
- La partícula disminuye su velocidad y luego, la incrementa.
Existe una velocidad inicial crítica v0,c para el cual la velocidad v de la partícula presenta un mínimo v=0 en el ángulo θc denominado ángulo crítico (véase la curva de color azul).
Tenemos un sistema de dos ecuaciones, haciendo operaciones y simplificando llegamos a la siguiente relación
tanθc=μ
Empleando las relaciones trigonométricas
calculamos la velocidad inicial crítica v0,c en θ=0 para la cual la partícula se detiene en θc.
Ejemplo
Para μ=1, y R=1
- v0,c =2.2522046 m/s
- El ángulo crítico es 45º
En la figura se representa v0,c en función del coeficiente de rozamiento μ
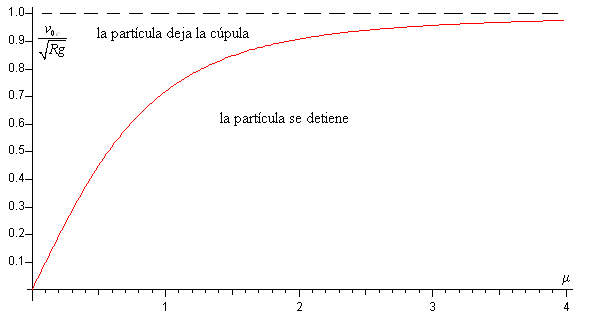
Como apreciamos en la gráfica,
La curva de color rojo divide el plano (μ, v0) en dos regiones. Fijado el valor de μ
- Para velocidades iniciales v0>v0,c la partícula no se detiene, deja la cúpula
- Para velocidades iniciales v0<v0,c la partícula se detiene.
Utilizando MATLAB
Integramos la ecuación diferencial de primer orden utilizando
Obtenemos las expresión de x para el caso en el que el coeficiente μ=1 de la fuerza de rozamiento
Representamos en la misma ventana gráfica x en función del ángulo t, en radianes, para varios valores de la velocidad inicial v0 o de la condición inicial x0
Calculamos mediante solve el valor de la velocidad inicial crítica para el ángulo θc tal que tanθc=μ
syms mu x0 t;
x=dsolve('Dx-2*mu*x=2*(sin(t)-mu*cos(t))','x(0)=x0');
x=subs(x,mu,1)
xf=[2.20 2.22 2.24 2.26 2.28 2.30].^2/9.8;
hold on
for i=1:length(xf)
xx=subs(x,x0,xf(i));
ezplot(xx,[0,50*pi/180]);
end
xlabel('\theta(radianes)')
ylabel('v^2/(Rg)')
title('Movimiento en un cúpula')
grid on
hold off
%calcula la velocidad inicial crítica para el ángulo t tal que tan(t)=mu
vc=sqrt(9.8*solve(subs(x,t,atan(1)),x0));
double(vc)
ans =2.2522
Balance energético
La energía de la partícula en la posición inicial es- La energía cinética Ek=mv02/2
-
La energía potencial Ep=mgR
Cuando la partícula se encuentra en la posición angular θ.
- La energía cinética Ek=mv2/2
- La energía potencial Ep=mgRcosθ
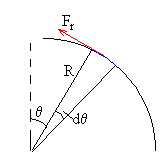
La fuerza de rozamiento Fr=μN, tiene la misma dirección (tangencial) que el desplazamiento, el arco R·dθ, pero de sentido contrario. El trabajo realizado por la fuerza de rozamiento es.
El trabajo realizado por la fuerza de rozamiento Wnc<0 también se puede calcular hallando la diferencia entre la energía final menos la energía inicial.
Resulta
derivando con respecto a θ
La misma ecuación diferencial que obtuvimos por dinámica
Solución numérica de la ecuación del movimiento
Primero, calculamos el ángulo límite para el cual la partícula se detiene v=0, o bien, la reacción de la cúpula N=0. Después, resolvemos la ecuación diferencial del movimiento que se ha deducido al principio de esta página.
function cupula_6
R=1; %radio
mu=0.4; %coeficiente de rozamiento
v0=2; %velocidad incial
Vc=sqrt(R*9.8*2*(2*mu^2-1+sqrt(mu^2+1)*exp(-2*mu*atan(mu)))/(1+4*mu^2));
v2=@(x) v0^2*exp(2*mu*x)/(R*9.8)+((4*mu^2-2)*(cos(x)-exp(2*mu*x))-
6*mu*sin(x))/(4*mu^2+1);
N=@(x) cos(x)-v2(x);
if v0<Vc
aLimite=fzero(v2,[0,pi/2]);
opts=odeset('events',@(t,x) stop_cupula_1(t,x));
else
aLimite=fzero(N,[0,pi/2]);
opts=odeset('events',@(t,x) stop_cupula(t,x));
end
x0=[0, v0];
f=@(t,x) [x(2);9.8*sin(x(1))/R-mu*(9.8*cos(x(1))-R*x(2)^2)/R];
tspan=[0,10];
[t,x]=ode45(f,tspan,x0,opts);
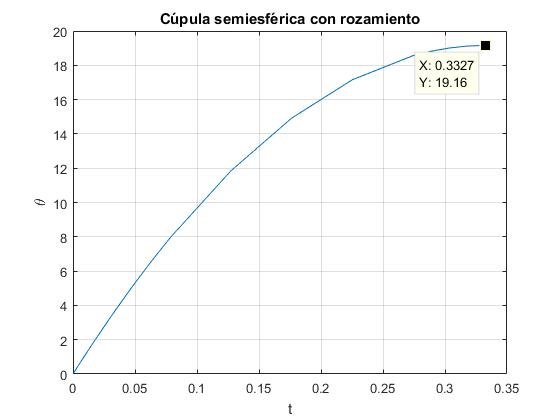
plot(t,x(:,1)*180/pi)
grid on
xlabel('t')
ylabel('\theta')
title('Cúpula semiesférica con rozamiento')
function [value,isterminal,direction]=stop_cupula(~,x)
value=aLimite-x(1);
isterminal=1;
direction=0;
end
function [value,isterminal,direction]=stop_cupula_1(~,x)
value=x(2);
isterminal=1;
direction=0;
end
end
Hemos definido dos funciones para que el proceso de integración se detenga cuando N sea cero o cuando la velocidad dθ/dt sea cero.
Cuando μ=0.4 y v0=2. La partícula deja de tener contacto con la cúpula, N=0 cuando θ=45.2°
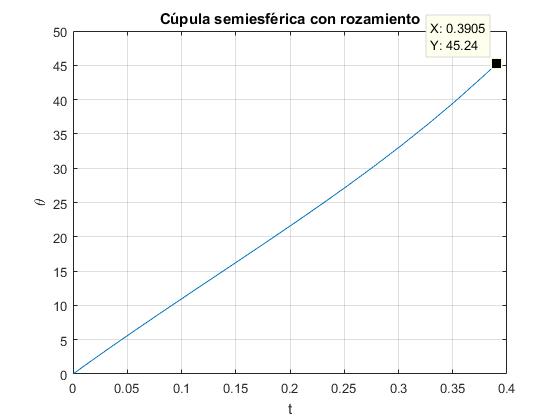
Cambiamos el coeficiente de rozamiento μ=1, la partícula se detiene dθ/dt=0, para θ=19.2°.
Ejemplo
- Rozamiento nulo, μ=0
- Rozamiento no nulo
Si la velocidad inicial es v0=1.5.
La partícula deja de tener contacto con la cúpula semiesférica en la posición θc=42º
Sea μ=0.3 y v0=1.8
La partícula deja de tener contacto con la cúpula para θc=46º, con v=2.61 y N≈0
La tarea del lector será la de investigar para qué valores de la velocidad inicial v0 y del coeficiente de rozamiento μ, hacen que θc sea tan próximo a 90º como sea posible. Compruébese el siguiente ejemplo: μ=1.0 y v0=2.257
Actividades
Se introduce
-
El coeficiente de rozamiento μ, en el control de edición titulado Rozamiento
-
La velocidad inicial v0 en la posición inicial θ=0, en el control de edición titulado V. inicial.
-
La masa de la partícula se ha fijado en m=1 kg
-
El radio de la cúpula se ha fijado en R=1 m.
Se pulsa el botón titulado Nuevo
Observamos el movimiento de la partícula deslizando sobre la cúpula. Sobre la partícula se dibujan las fuerzas: peso mg, reacción N, y fuerza de rozamiento Fr.
En la parte superior derecha, se proporcionan los datos de
- el tiempo t en segundos
- la posición angular θ en grados
- la velocidad v de la partícula en m/s.
Cuando la reacción N se hace cero, se muestran los datos de la a velocidad v en la posición θc en la que la partícula deja de tener contacto con la cúpula semiesférica.
El círculo situado en la parte superior izquierda representa la energía total de la partícula, la porción de color rojo representa la energía cinética, y la porción azul, la energía potencial. Observamos que la energía potencial se va transformando en energía cinética, pero la suma de los valores de ambas clases de energía no se mantiene constante a lo largo de la trayectoria de la partícula si hay rozamiento. El trabajo de la fuerza de rozamiento viene indicado por la porción negra del círculo de mayor radio.
Mediante una línea roja a trazos se señala el ángulo límite, para el cual la reacción N=0 o la partícula se detiene, su velocidad v=0
Referencias
Mungan C. Sliding on the surface of a rough sphere. The Physics Teacher, Vol 41, September 2003, pp. 326-328
Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017
de Lange O. L. Pierrus J., Prior T., Mele E. J. Comment on “A block slipping on a sphere with friction: Exact and perturbative solutions”, by Tom Prior and E. J. Mele [Am. J. Phys. 75 (5) 423-426 (2007)] Am. J. Phys. 76 (1) January 2008.

