Modos normales de vibración de sistemas lineales heterogéneos.
Sistema formado por partículas de la misma masa unidas por muelles elásticos de distinta constante
En la página titulada Modos normales de vibración (II), se ha estudiado un sistema formado por partículas de la misma masa unidas por muelles elásticos de distinta constante. En la figura se muestra un sistema formado por N partículas de masa m unidas a muelles de constante k (azul) y g (rojo) alternados

Un muelle de constante k une los puntos 1 y 2. La relación entre el estado del punto 2 y del punto 1 es
Una partícula de masa m une los puntos 2 y 3. La relación entre el estado del punto 3 y del punto 2 es
-
Un muelle de constante g une los puntos 3 y 4. La relación entre el estado del punto 4 y del punto 3 es
donde Tg representa la matriz correspondiente al muelle de constante g, Tk representa al muelle de constante k y Tp a la partícula de masa m.
Continuamos hasta llegar al punto final 2N+2, relacionando mediante la matriz T el estado del punto final 2N+2 con el estado del punto 1
Para un sistema de N=4 partículas
![]()
Para un sistema de N=5 partículas

Condiciones de contorno
Para N=5, las condiciones de contorno son:
- x1=0, ya que el punto 1 es fijo
- x12=0, ya que el extremo 12 es fijo
Lo que implica que el elemento de la matriz T12=0
En la página titulada Modos normales de vibración (II) disponemos de un programa interactivo que calcula las frecuencias de los modos normales de vibración del sistema formado por N=5 partículas de masas m=1 unidas a muelles elásticos de constante k=1 (azules) y g=2 (rojos), y representa el MAS que describe cada una de las partículas para el modo de vibración seleccionado
Frecuencias de los modos normales de oscilación
Utilizamos Math Symbolic de Matlab para realizar la multiplicación de matrices
syms k g m w;
N=5; %número de partículas
Tk=[1,1/k;0,1];
Tg=[1,1/g;0,1];
Tp=[1,0;-m*w^2,1];
T=eye(2);
for i=1:2:N
T=(Tp*Tk)*T;
if i==N
break;
end
T=(Tp*Tg)*T;
end
if rem(N,2)==0
T=Tk*T;
else
T=Tg*T;
end
masa=1; %masa
cte_k=1; %constante del muelle azul
cte_g=2; %constante del muelle rojo
V=subs(T,{k,g,m},{cte_k,cte_g,masa});
W=double(solve(V(1,2))); %complejas
Wr=zeros(N,1); %reales
j=1;
for i=1:length(W)
if real(W(i))>0
Wr(j)=real(W(i));
j=j+1;
end
end
Wr=sort(Wr); %frecuencias
disp(Wr)
0.5952
1.1260
1.7321
2.1753
2.3761
Comprobamos que el determinante de la matriz T es la unidad
>> det(T) ans =1
Amplitudes del MAS que describe de cada una de las partículas
- La amplitud de la primera partícula es q1=x2=x3
- La amplitud de la segunda partícula es q2=x4=x5
- La amplitud de la tercera partícula es q3=x6=x7
- La amplitud de la cuarta partícula es q4=x8=x9
- La amplitud de la quinta partícula es q5=x10=x11
Una vez que se han calculado las amplitudes qj con j=1,2,...N, de cada una de las partículas se normalizan de acuerdo a la siguiente fórmula
donde mj es la masa de cada partícula
Completamos el script anterior para calcular y representar las amplitudes de la oscilación de cada una de las partículas para la frecuencia del modo seleccionado
....
q=zeros(N,1);
Vk=subs(Tk,k,cte_k);
Vg=subs(Tg,g,cte_g);
w1=Wr(1); %frecuencia del primer modo de vibración
Vp=subs(Tp,{m,w},{masa,w1});
V=eye(2);
suma=0;
for j=1:N
if rem(j,2)==0
V=(Vp*Vg)*V;
else
V=(Vp*Vk)*V;
end
q(j)=[1,0]*V*[0;1];
suma=suma+masa*q(j)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
stem(q);
xlim([0,N+1])
xlabel('j')
ylabel('q_j')
title(num2str(w1))
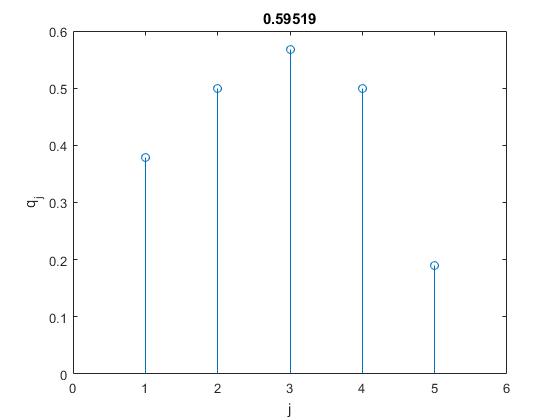
Calculamos las amplitudes qj(ωr) con j=1,2,...N para la frecuencia ωr de un modo normal de vibración y las amplitudes qj(ωs) para la frecuencia ωs de otro modo normal de vibración r≠s. Comprobamos que se cumple que
Hemos calculado las amplitudes qj para la frecuencia del modo fundamental ω1. Duplicamos el código para calcular las amplitudes yj para el tercer modo de vibración ω3
...
q=zeros(N,1);
Vk=subs(Tk,k,cte_k);
Vg=subs(Tg,g,cte_g);
w1=Wr(1); %frecuencia del primer modo de vibración
Vp=subs(Tp,{m,w},{masa,w1}); %frecuencia del primer modo de vibración
V=eye(2);
suma=0;
for j=1:N
if rem(j,2)==0
V=(Vp*Vg)*V;
else
V=(Vp*Vk)*V;
end
q(j)=[1,0]*V*[0;1];
suma=suma+masa*q(j)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
w2=Wr(3); %frecuencia del tercer modo de vibración
Vp=subs(Tp,{m,w},{masa,w2});
V=eye(2);
suma=0;
y=zeros(N,1);
for j=1:N
if rem(j,2)==0
V=(Vp*Vg)*V;
else
V=(Vp*Vk)*V;
end
y(j)=[1,0]*V*[0;1];
suma=suma+masa*y(j)^2;
end
for j=1:N
y(j)=y(j)/sqrt(suma);
end
%comprobación
suma=0;
for j=1:N
suma=suma+y(j)*q(j);
end
disp(suma)
-3.3307e-16
Oscilaciones de una cadena diatómica lineal
En la página titulada Modos normales de vibración (II), se ha estudiado un sistema formado por partículas de masas alternadas (negra y roja) unidas por muelles elásticos de la misma constante. Sea el sistema formado por N partículas de masa m y M unidas a muelles de constante k

Un muelle de constante k une los puntos 1 y 2. La relación entre el estado del punto 2 y del punto 1 es
Una partícula de masa m une los puntos 2 y 3. La relación entre el estado del punto 3 y del punto 2 es
Un muelle de constante k une los puntos 3 y 4. La relación entre el estado del punto 4 y del punto 3 es
Una partícula de masa M une los puntos 2 y 3. La relación entre el estado del punto 3 y del punto 2 es
donde Ts representa la matriz correspondiente al muelle de constante k, Tm representa a la partícula de masa m y TM a la partícula de masa M.
Continuamos hasta llegar al punto final 2N+2, relacionado mediante la matriz T el estado del punto final 2N+2 con el estado del punto 1
Para un sistema de N=4 partículas

Para un sistema de N=5 partículas

Condiciones de contorno
Las condiciones de contorno son:
- x1=0, ya que el punto 1 es fijo
- x12=0, ya que el extremo 12 es fijo
Lo que implica que el elemento de la matriz T12=0
En la página titulada Modos normales de vibración (II) disponemos de un programa interactivo que calcula las frecuencias de los modos normales de vibración del sistema formado por N=5 partículas de masas m=1 y M=2 unidas a muelles elásticos de constante k=1 y representa el MAS que describe cada una de las partículas para el modo de vibración seleccionado
Frecuencias de los modos normales de oscilación
Utilizamos Math Symbolic de Matlab para realizar la multiplicación de matrices
syms k m M w;
N=5; %número de partículas
Ts=[1,1/k;0,1];
Tm=[1,0;-m*w^2,1];
TM=[1,0;-M*w^2,1];
T=eye(2);
for i=1:2:N
T=(Tm*Ts)*T;
if i==N
break;
end
T=(TM*Ts)*T;
end
T=Ts*T;
masa_1=1; %masa
masa_2=2;
cte=1; %constante del muelle azul
V=subs(T,{k,m,M},{cte, masa_1,masa_2});
W=double(solve(V(1,2))); %complejas
Wr=zeros(N,1); %reales
j=1;
for i=1:length(W)
if real(W(i))>0
Wr(j)=real(W(i));
j=j+1;
end
end
Wr=sort(Wr); %frecuencias
disp(Wr)
0.4209
0.7962
1.4142
1.5382
1.6801
Comprobamos que el determinante de la matriz T es la unidad
>> det(T) ans =1
Amplitudes del MAS que describe de cada una de las partículas
- La amplitud de la primera partícula es q1=x2=x3
- La amplitud de la segunda partícula es q2=x4=x5
- La amplitud de la tercera partícula es q3=x6=x7
- La amplitud de la cuarta partícula es q4=x8=x9
- La amplitud de la quinta partícula es q5=x10=x11
Una vez que se han calculado las amplitudes qj con j=1,2,...N, de cada una de las partículas se normalizan de acuerdo a la siguiente fórmula
donde mj es la masa de cada partícula
Completamos el script anterior para calcular y representar las amplitudes de la oscilación de cada una de las partículas para la frecuencia del modo seleccionado
....
q=zeros(N,1);
Vs=subs(Ts,k,cte);
w1=Wr(1); %frecuencia del primer modo de vibración
Vm=subs(Tm,{m,w},{masa_1,w1});
VM=subs(TM,{M,w},{masa_2,w1});
V=eye(2);
suma=0;
for j=1:2:N
V=(Vm*Vs)*V;
q(j)=[1,0]*V*[0;1];
suma=suma+masa_1*q(j)^2;
if j==N
break;
end
V=(VM*Vs)*V;
q(j+1)=[1,0]*V*[0;1];
suma=suma+masa_2*q(j+1)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
stem(q);
xlim([0,N+1])
xlabel('j')
ylabel('q_j')
title(num2str(w1))
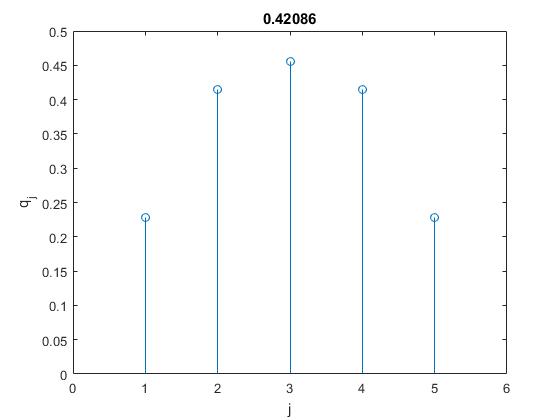
Calculamos las amplitudes qj(ωr) con j=1,2,...N para la frecuencia ωr de un modo normal de vibración y las amplitudes qj(ωs) para la frecuencia ωs de otro modo normal de vibración r≠s. Comprobamos que se cumple que
Hemos calculado las amplitudes qj para la frecuencia del modo fundamental ω1. Duplicamos el código para calcular las amplitudes yj para el tercer modo de vibración ω3
...
q=zeros(N,1);
Vs=subs(Ts,k,cte);
w1=Wr(1); %frecuencia del primer modo de vibración
Vm=subs(Tm,{m,w},{masa_1,w1});
VM=subs(TM,{M,w},{masa_2,w1});
V=eye(2);
suma=0;
for j=1:2:N
V=(Vm*Vs)*V;
q(j)=[1,0]*V*[0;1];
suma=suma+masa_1*q(j)^2;
if j==N
break;
end
V=(VM*Vs)*V;
q(j+1)=[1,0]*V*[0;1];
suma=suma+masa_2*q(j+1)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
y=zeros(N,1);
Vs=subs(Ts,k,cte);
w2=Wr(3); %frecuencia del tercer modo de vibración
Vm=subs(Tm,{m,w},{masa_1,w2});
VM=subs(TM,{M,w},{masa_2,w2});
V=eye(2);
suma=0;
for j=1:2:N
V=(Vm*Vs)*V;
y(j)=[1,0]*V*[0;1];
suma=suma+masa_1*q(j)^2;
if j==N
break;
end
V=(VM*Vs)*V;
y(j+1)=[1,0]*V*[0;1];
suma=suma+masa_2*y(j+1)^2;
end
for j=1:N
y(j)=y(j)/sqrt(suma);
end
%comprobación
suma=0;
for j=1:2:N
suma=suma+masa_1*q(j)*y(j);
if j==N
break;
end
suma=suma+masa_2*q(j+1)*y(j+1);
end
disp(suma)
5.5511e-17
Cadena lineal con un defecto
Consideremos un sistema formado por N partículas de masa m unidas a muelles de constante k. Se ha sustituido la partícula situada en la posición d por otra partícula de masa M distinta. Vamos a comprobar el efecto que tiene este cambio en los modos normales de vibración
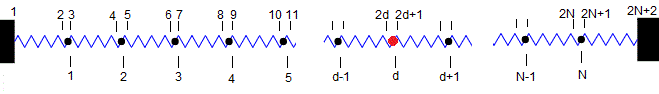
La relación entre los estados de los puntos 2,3, ...2d, 2d+1,....2N+1, 2N+2, señalados en la parte superior de la figura con el estado del punto 1 es la siguiente
donde
Condiciones de contorno
Las condiciones de contorno son:
- x1=0, ya que el punto 1 es fijo
- x2N+2=0, ya que el extremo N+2 es fijo
Lo que implica que el elemento de la matriz T12=0
Sea el sistema formado por N=20 partículas de masas m=4 unidas a muelles elásticos de constante k=1 se sustituye la partícula d=7 por otra partícula de masa M=1. Calculamos las frecuencias de los modos normales de vibración
Frecuencias de los modos normales de oscilación
Utilizamos Math Symbolic de Matlab para realizar la multiplicación de matrices
Masa=1; %defecto
cte=1;
d=7; %posición del defecto
Ts=[1,1/k;0,1]; %masa
Tp=[1,0;-m*w^2,1]; %partícula
Td=[1,0;-M*w^2,1]; %defecto
T=Ts*(Tp*Ts)^(N-d)*(Td*Ts)*(Tp*Ts)^(d-1);
V=subs(T,{k,m,M},{cte,masa,Masa});
W=double(solve(V(1,2))); %complejas
Wr=zeros(N,1); %reales
j=1;
for i=1:length(W)
if real(W(i))>0
Wr(j)=real(W(i));
j=j+1;
end
end
Wr=sort(Wr);
disp(Wr)
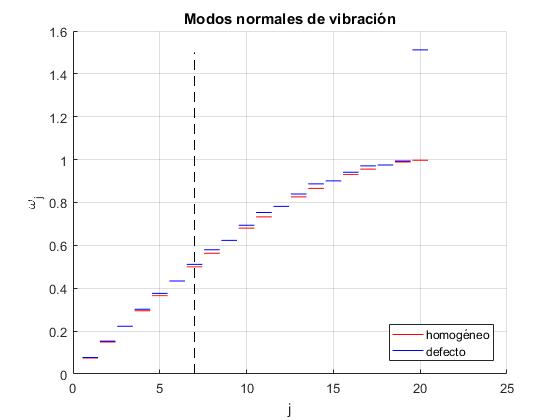
Comparamos los niveles de energía con defecto y sin defecto
| orden | homogénea | defecto |
|---|---|---|
| 1 | 0.0747 | 0.0767 |
| 2 | 0.1490 | 0.1533 |
| 3 | 0.2225 | 0.2225 |
| 4 | 0.2948 | 0.3022 |
| 5 | 0.3653 | 0.3760 |
| 6 | 0.4339 | 0.4339 |
| 7 | 0.5000 | 0.5114 |
| 8 | 0.5633 | 0.5796 |
| 9 | 0.6235 | 0.6235 |
| 10 | 0.6802 | 0.6936 |
| 11 | 0.7331 | 0.7532 |
| 12 | 0.7818 | 0.7818 |
| 13 | 0.8262 | 0.8394 |
| 14 | 0.8660 | 0.8866 |
| 15 | 0.9010 | 0.9010 |
| 16 | 0.9309 | 0.9412 |
| 17 | 0.9556 | 0.9710 |
| 18 | 0.9749 | 0.9749 |
| 19 | 0.9888 | 0.9934 |
| 20 | 0.9972 | 1.5119 |
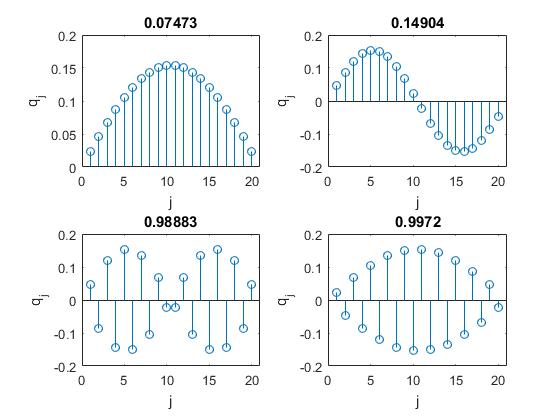
Comparamos los dos conjuntos de frecuencias de forma gráfica, en el eje horizontal el número de modo normal de vibración, en el eje vertical, la frecuencia. En color rojo el sistema homogéneo. Cuando se sustituye la partícula d=7 (marcada en línea a trazos) por otra de masa más pequeña, las frecuencias se modifican y se representan en color azul
defecto=[0.0767, 0.1533, 0.2225, 0.3022, 0.3760,
0.4339, 0.5114, 0.5796, 0.6235, 0.6936, 0.7532, 0.7818, 0.8394, 0.8866,
0.9010, 0.9412, 0.9710, 0.9749, 0.9934, 1.5119];
lineal=[0.0747, 0.1490, 0.2225, 0.2948, 0.3653, 0.4339, 0.5000, 0.5633, 0.6235,
0.6802, 0.7331, 0.7818, 0.8262, 0.8660, 0.9010, 0.9309, 0.9556,
0.9749, 0.9888, 0.9972];
for j=1:length(lineal)
line([j-0.45,j+0.45],[lineal(j),lineal(j)],'color','r')
line([j-0.45,j+0.45],[defecto(j),defecto(j)],'color','b')
end
line([7,7],[0,1.5],'color','k','lineStyle','--')
legend('homogéneo','defecto', 'location','southeast')
grid on
xlabel('j')
ylabel('\omega_j')
title('Modos normales de vibración')
Comprobamos que el determinante de la matriz T es la unidad
>> det(T) ans =1
Amplitudes del MAS que describe de cada una de las partículas
- La amplitud de la primera partícula es q1=x2=x3
- La amplitud de la segunda partícula es q2=x4=x5
- La amplitud de la tercera partícula es q3=x6=x7
- ...
Una vez que se han calculado las amplitudes qj con j=1,2,...N, de cada una de las partículas se normalizan de acuerdo a la siguiente fórmula
donde mj es la masa de cada partícula
Completamos el script anterior para calcular y representar las amplitudes de la oscilación de cada una de las partículas para la frecuencia del modo seleccionado
....
w1=Wr(7); %frecuencia del modo siete de vibración
Vs=subs(Ts,k,cte);
Vp=subs(Tp,{m,w},{masa,w1});
Vd=subs(Td,{M,w},{Masa,w1});
q=zeros(N,1);
suma=0;
for j=1:d-1
q(j)=[1,0]*(Vp*Vs)^j*[0;1];
suma=suma+masa*q(j)^2;
end
%defecto
V0=(Vd*Vs)*(Vp*Vs)^(d-1);
q(d)=[1,0]*V0*[0;1];
suma=suma+Masa*q(d)^2;
for j=d+1:N
q(j)=[1,0]*(Vp*Vs)^(j-d)*V0*[0;1];
suma=suma+masa*q(j)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
grid on
stem(q);
xlim([0,N+1])
xlabel('j')
ylabel('q_j')
title(num2str(w1))
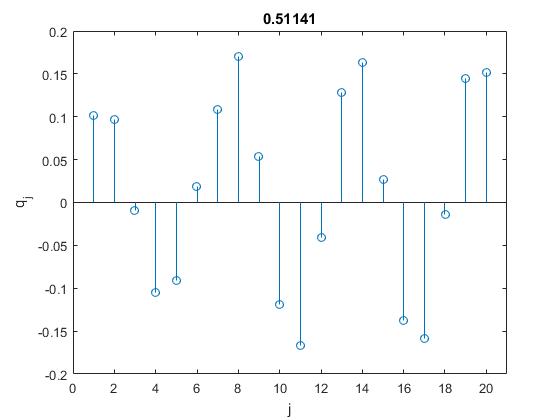
En el siguiente script representamos las amplitudes qj de los dos primeros modos de vibración y de los dos últimos modos para un sistema de N=20 partículas, de masa m=4 unidas a muelles de constante k=1. En el título de cada uno de los gráficos aparece la frecuencia
syms k m M w;
N=20; %número de partículas
masa=4; %masa de las partículas excepto
Masa=1; %defecto
cte=1;
d=7; %posición del defecto
Ts=[1,1/k;0,1]; %masa
Tp=[1,0;-m*w^2,1]; %partícula
Td=[1,0;-M*w^2,1]; %defecto
T=Ts*(Tp*Ts)^(N-d)*(Td*Ts)*(Tp*Ts)^(d-1);
V=subs(T,{k,m,M},{cte,masa,Masa});
W=double(solve(V(1,2))); %complejas
Wr=zeros(N,1); %reales
j=1;
for i=1:length(W)
if real(W(i))>0
Wr(j)=real(W(i));
j=j+1;
end
end
Wr=sort(Wr);
disp(Wr)
%amplitudes
q=zeros(N,1);
Vs=subs(Ts,k,cte);
ventana=1;
for s=[1,2,19,20] % modos seleccionados
w1=Wr(s); %frecuencia del modo siete de vibración
Vp=subs(Tp,{m,w},{masa,w1});
Vd=subs(Td,{M,w},{Masa,w1});
suma=0;
for j=1:d-1
q(j)=[1,0]*(Vp*Vs)^j*[0;1];
suma=suma+masa*q(j)^2;
end
%defecto
V0=(Vd*Vs)*(Vp*Vs)^(d-1);
q(d)=[1,0]*V0*[0;1];
suma=suma+Masa*q(d)^2;
for j=d+1:N
q(j)=[1,0]*(Vp*Vs)^(j-d)*V0*[0;1];
suma=suma+masa*q(j)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
subplot(2,2,ventana)
stem(q);
xlim([0,N+1])
xlabel('j')
ylabel('q_j')
title(num2str(w1))
ventana=ventana+1;
end
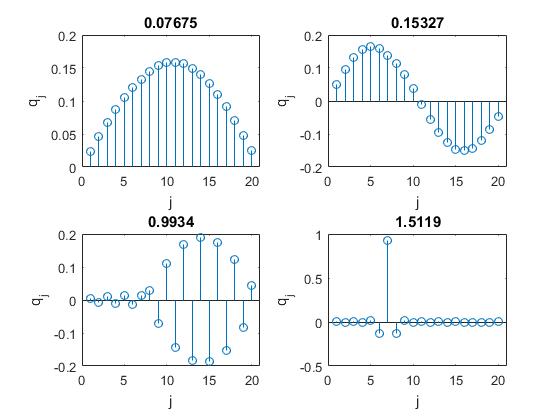
Los dos últimos modos difieren considerablemente del sistema homogéneo, véase al final de la página el apartado Sistema homogéneo o la figura que generó el script
Calculamos las amplitudes qj(ωr) con j=1,2,...N para la frecuencia ωr de un modo normal de vibración y las amplitudes qj(ωs) para la frecuencia ωs de otro modo normal de vibración r≠s. Comprobamos que se cumple que
Hemos calculado las amplitudes qj para la frecuencia del modo fundamental ω1. Duplicamos el código para calcular las amplitudes yj del modo 19 de vibración ω19
...
%amplitudes
w1=Wr(1); %frecuencia del modo 1 de vibración
Vs=subs(Ts,k,cte);
Vp=subs(Tp,{m,w},{masa,w1});
Vd=subs(Td,{M,w},{Masa,w1});
q=zeros(N,1);
suma=0;
for j=1:d-1
q(j)=[1,0]*(Vp*Vs)^j*[0;1];
suma=suma+masa*q(j)^2;
end
%defecto
V0=(Vd*Vs)*(Vp*Vs)^(d-1);
q(d)=[1,0]*V0*[0;1];
suma=suma+Masa*q(d)^2;
for j=d+1:N
q(j)=[1,0]*(Vp*Vs)^(j-d)*V0*[0;1];
suma=suma+masa*q(j)^2;
end
for j=1:N
q(j)=q(j)/sqrt(suma);
end
w2=Wr(19); %frecuencia del modo 19 de vibración
Vs=subs(Ts,k,cte);
Vp=subs(Tp,{m,w},{masa,w2});
Vd=subs(Td,{M,w},{Masa,w2});
y=zeros(N,1);
suma=0;
for j=1:d-1
y(j)=[1,0]*(Vp*Vs)^j*[0;1];
suma=suma+masa*q(j)^2;
end
%defecto
V0=(Vd*Vs)*(Vp*Vs)^(d-1);
y(d)=[1,0]*V0*[0;1];
suma=suma+Masa*q(d)^2;
for j=d+1:N
y(j)=[1,0]*(Vp*Vs)^(j-d)*V0*[0;1];
suma=suma+masa*q(j)^2;
end
for j=1:N
y(j)=y(j)/sqrt(suma);
end
%comprobación
suma=0;
for j=1:d-1
suma=suma+masa*q(j)*y(j);
end
suma=suma+Masa*q(d)*y(d);
for j=d+1:N
suma=suma+masa*q(j)*y(j);
end
disp(suma)
-5.1070e-15
Cuando relacionamos cualquier otro modo de vibración, por ejemplo el primer modo, con el modo 20, el resultado de la suma es
0.0018
Un incremento considerable del error en la suma que debería dar próximo a cero, como en los demás casos
Referencias
Para el último apartado, Cadena lineal con un defecto
Amy Kolan, barry Cipra, Bill Titus. Exploring localization in nonperiodic systems. Computer in Physics, (9) 4, jul/aug 1995, pp. 387-395

