Cadena monoatómica lineal

Como vemos en la figura tenemos N partículas de masa m unidas a N+1 muelles iguales de constante k, cuyos extremos están fijos. La separación de equilibrio entre las partículas es a.

Supongamos que en un instante dado t, la partícula 1 se desplaza x₁, la partícula 2 se desplaza x₂, ... la partícula i se desplaza x_i, etc.

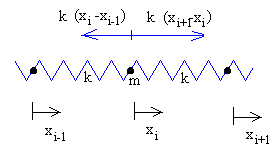
La ecuación del movimiento para la partícula i será entonces

${\displaystyle \begin{array}{l}m\frac{d^2{x}_i}{d{t}^2}=-k(x_i-x_{i-1})+k(x_{i+1}-x_i)\\ m\frac{d^2{x}_i}{d{t}^2}=k{x}_{i-1}-2k{x}_i+k{x}_{i+1}\end{array}}$

i=1,2,3...N, x₀=0, x_N+1=0

Supongamos, que el sistema vibra en un modo de frecuencia ω. Cada partícula describirá un M.A.S. de la misma frecuencia ω , pero cuya amplitud A_i vamos a calcular.

x_i=A_i·cos(ω t)

Introduciendo esta expresión en la ecuación diferencial que describe el movimiento de cada partícula, obtenemos, la relación de recurrencia.

${\displaystyle \begin{array}{l}{A}_{i+1}+A_{i-1}=A_i\left(2-\frac{m}{k}{\omega }^2\right)A_0=0A_{N+1}=0\\ A_{i+1}-2s{A}_i+A_{i-1}=\mathrm{0,}s=1-\frac{m}{2k}{\omega }^2\end{array}}$

Vamos a calcular las frecuencias ω_n por dos procedimientos

Sistema homogéneo de ecuaciones

• Sistema formado por dos partículas, N=2

${\displaystyle N=2\{\begin{array}{l}{A}_2-2s{A}_1+A_0=0\\ A_3-2s{A}_2+A_1=0\end{array}\{\begin{array}{l}{A}_2-2s{A}_1=0\\ -2s{A}_2+A_1=0\end{array}}$

Se trata de un sistema homogéneo de dos ecuaciones con dos incógnitas. El determinante de los coeficientes es cero

${\displaystyle \left|\begin{array}{cc}1& -2s\\ -2s& 1\end{array}\right|=\mathrm{0,}4s^2-1=0\{\begin{array}{l}s=1/2\\ s=-1/2\end{array}}$

Conocido s=1-mω²/(2k), despejamos ω² y obtenemos las frecuencias de los modos normales para N=2

${\displaystyle {\omega }_1=\sqrt{\frac{k}{m}},{\omega }_2=\sqrt{3\frac{k}{m}}}$

syms s;
eq=det([1,-2*s;-2*s,1]);
sol=solve(eq);
w=sqrt(2*(1-sol));

w = 
 3^(1/2)
       1

• Sistema formado por tres partículas, N=3

${\displaystyle \begin{array}{l}N=3\{\begin{array}{l}{A}_2-2s{A}_1+A_0=0\\ A_3-2s{A}_2+A_1=0\\ A_4-2s{A}_3+A_2=0\end{array}\{\begin{array}{l}{A}_2-2s{A}_1=0\\ A_3-2s{A}_2+A_1=0\\ -2s{A}_3+A_2=0\end{array}\hfill \\ \left|\begin{array}{ccc}0& 1& -2s\\ 1& -2s& 1\\ -2s& 1& 0\end{array}\right|=\mathrm{0,}2s^3-s=0\{\begin{array}{l}s=0\\ s=1/\sqrt{2}\\ s=-1/\sqrt{2}\end{array}\hfill \end{array}}$

Conocido s despejamos ω² y obtenemos las frecuencias de los modos normales para N=3

${\displaystyle {\omega }_1=\sqrt{\left(2-\sqrt{2}\right)\frac{k}{m}},{\omega }_2=\sqrt{2\frac{k}{m}},{\omega }_3=\sqrt{\left(2+\sqrt{2}\right)\frac{k}{m}}}$

syms s;
eq=det([0,1,-2*s;1,-2*s,1;-2*s,1,0]);
sol=solve(eq);
w=sqrt(2*(1-sol))

w =
             2^(1/2)
 (2^(1/2) + 2)^(1/2)
 (2 - 2^(1/2))^(1/2)

• Sistema formado por cuatro partículas, N=4

${\displaystyle \begin{array}{l}N=4\{\begin{array}{l}{A}_2-2s{A}_1+A_0=0\\ A_3-2s{A}_2+A_1=0\\ A_4-2s{A}_3+A_2=0\\ A_5-2s{A}_4+A_3=0\end{array}\{\begin{array}{l}{A}_2-2s{A}_1=0\\ A_3-2s{A}_2+A_1=0\\ A_4-2s{A}_3+A_2=0\\ -2s{A}_4+A_3=0\end{array}\\ \left|\begin{array}{cccc}0& 0& 1& -2s\\ 0& 1& -2s& 1\\ 1& -2s& 1& 0\\ -2s& 1& 0& 0\end{array}\right|=\mathrm{0,}16s^4-12s^2+1=0\{\begin{array}{l}-\frac{1}{4}\left(\sqrt{5}+1\right)\\ -\frac{1}{4}\left(\sqrt{5}-1\right)\\ \frac{1}{4}\left(\sqrt{5}-1\right)\\ \frac{1}{4}\left(\sqrt{5}+1\right)\end{array}\end{array}}$

Conocido s despejamos ω² y obtenemos las frecuencias de los modos normales para N=4

${\displaystyle \begin{array}{l}{\omega }_1=\sqrt{\left(\frac{3-\sqrt{5}}{2}\right)\frac{k}{m}},{\omega }_2=\sqrt{\left(\frac{3+\sqrt{5}}{2}\right)\frac{k}{m}},\\ {\omega }_3=\sqrt{\left(\frac{5-\sqrt{5}}{2}\right)\frac{k}{m}},{\omega }_4=\sqrt{\left(\frac{5+\sqrt{5}}{2}\right)\frac{k}{m}}\end{array}}$

syms s;
eq=det([0,0,1,-2*s;0,1,-2*s,1;1,-2*s,1,0;-2*s,1,0,0]);
sol=solve(eq);
w=sqrt(2*(1-sol))

w =
 (5^(1/2)/2 + 5/2)^(1/2)
 (5^(1/2)/2 + 3/2)^(1/2)
 (5/2 - 5^(1/2)/2)^(1/2)
 (3/2 - 5^(1/2)/2)^(1/2)
>> double(w)'
ans =    1.9021    1.6180    1.1756    0.6180

Creamos un script para calcular ω_n para cualquier valor de N

syms s;
N=5; %número de partículas
matriz=-2*s*eye(N);
for i=2:N-1
    matriz(i,i+1)=1;
    matriz(i,i-1)=1;
end
matriz(1,2)=1;
matriz(N,N-1)=1;
eq=det(matriz);
sol=solve(eq);
w=sqrt(2*(1-sol));
double(w)'

w =
             3^(1/2)
             2^(1/2)
                   1
 (3^(1/2) + 2)^(1/2)
 (2 - 3^(1/2))^(1/2)
 
ans =    1.7321    1.4142    1.0000    1.9319    0.5176

Polinomios de Chebyshev

Tomando A₀=0 y A₁=1, las relación de recurrencia nos proporciona los coeficientes A₂, A₃...

${\displaystyle \begin{array}{l}\begin{array}{l}{A}_1=1\\ A_2=2s{A}_1-A_0=2s\end{array}\hfill \\ A_3=2s{A}_2-A_1=4s^2-1\hfill \\ A_4=2s{A}_3-A_2=8s^3-4s\hfill \\ \begin{array}{l}{A}_5=2s{A}_4-A_3=16s^4-12s^2+1\\ \mathrm{.....}\end{array}\hfill \\ \begin{array}{l}{A}_{N+1}=2s{A}_N-A_{N-1}\\ U_N=2s{U}_{N-1}-U_{N-2}\end{array}\hfill \end{array}}$

Si vamos al final de la página los polinomios de Chebyshev de segunda especie veremos que A₁ se corresponde con el polinomio U₀, A₂ con el polinomio U₁... A_N+1=0 (extremo fijo) con U_N(s). Las raíces del polinomio U_N(s) nos dan las frecuencias ω_n de los modos de vibración que vamos a calcular a continuación

Creamos un script para obtener los coeficientes del polinomio U_N(s). Mediante la función roots de MATLAB calculamos sus raíces y a continuación, las frecuencias ω_n. Supondremos que k/m=1

N=5; %número de partículas
A=zeros(N,1);
A0=[0];
A1=[1];
for i=2:N+1
    A=2*[A1,0]-[0,A0];
    A0=[0,A1];
    A1=A;
end
sol=roots(A);
w=sqrt(2*(1-sol));
disp(w')

w =    0.5176    1.0000    1.4142    1.7321    1.9319

Alternativamente, calculamos las raíces del polinomio de Chebyshev U_N(s) a través de su definición,

${\displaystyle \begin{array}{l}\begin{array}{l}\begin{array}{l}{U}_N(s)=\frac{\sin \left((N+1)\theta \right)}{\sin \theta }=0\\ {\theta }_n=\frac{n\pi }{N+1}n=\mathrm{1,2,3...}N\end{array}\hfill \\ s_n=\cos \left(\frac{n\pi }{N+1}\right)\hfill \\ 1-\frac{m}{2k}{\omega }_n^2=s_n\hfill \end{array}\hfill \\ {\omega }_n=2\sqrt{\frac{k}{m}}\sin \left(\frac{n\pi }{N+1}\right)\hfill \end{array}}$

Las frecuencias ω_n para N=5 partículas

N=5;
n=1:N;
w=2*sin(n*pi/(2*(N+1)))

w =    0.5176    1.0000    1.4142    1.7321    1.9319

En un sistema de N partículas de masa m unidas a N+1 muelles elásticos de constante k, los extremos fijos tienen amplitudes A₀=0 y A_N+1=0

Para cada frecuencia ω_n (n=1,2,3...N) calculamos las amplitudes: A₁, A₂,A₃...A_N o bien, los valores de los polinomios de Chebyshev U₀(s)=1, U₁(s), U₂(s),...U_N-1(s) para cada valor de s_n.

${\displaystyle A_i=U_{i-1}(s_n)=\frac{\sin \left(i·{\theta }_n\right)}{\sin {\theta }_n}=\frac{\sin \left(i·\frac{n\pi }{N+1}\right)}{\sin \left(\frac{n\pi }{N+1}\right)}i=\mathrm{1,2,3..}N}$

Una vez calculadas las amplitudes A_i, se multiplican por un factor para que la suma de sus cuadrados sea la unidad

${\displaystyle {\displaystyle \sum _{i=1}^N{A}_i^2}=1}$

Finalmente, queda multiplicar la amplitud de cada partícula i, A_icos(ω_nt) para observar el modo n de vibración de las N partículas unidas a N+1 muelles elásticos, tal como se ve en el programa interactivo de la página titulada Modos normales de vibración (I)

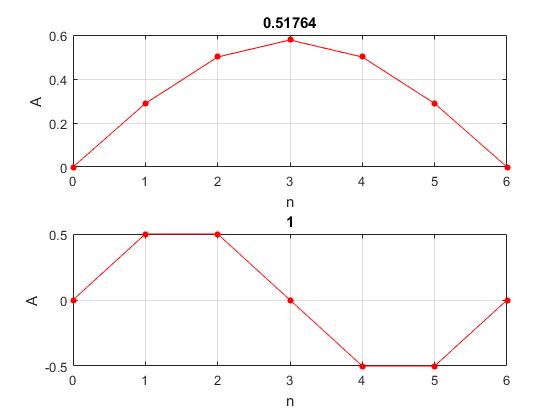
Suponiendo que k/m=1, representamos los dos primeros modos de vibración para un sistema de N=5 partículas. En el título de cada gráfica se proporcionan las frecuencias ω₁ y ω₂. Cambiando el índice n de 1 ... 5 se representan otros modos de vibración

Comprobamos en la página titulada Modos normales de vibración (I) que los valores de las frecuencias coinciden con las obtenidos por otros procedimientos (matricial)

N=5; %número de partículas
wn=2*sin((1:N)*pi/(2*N+2)); %frecuencias

subplot(2,1,1)
n=1; %primer modo de vibración
i=1:N;  %partículas
A=sin(i*n*pi/(N+1))/sin(n*pi/(N+1)); %U_0, U_1, ... U_N-1
suma=sum(A.^2);
A=A/sqrt(suma);
plot(0:N+1,[0,A,0],'-ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
xlim([0,N+1])
grid on
xlabel('n')
ylabel('A')
title(num2str(wn(n))) %frecuencia

subplot(2,1,2)
n=2; %segundo modo de vibración
i=1:N; %partículas
A=sin(i*n*pi/(N+1))/sin(n*pi/(N+1)); %valor del polinomio U_i correspondiente a w_n
suma=sum(A.^2);
A=A/sqrt(suma);
plot(0:N+1,[0,A,0],'-ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
xlim([0,N+1])
grid on
xlabel('n')
ylabel('A')
title(num2str(wn(n))) %frecuencia

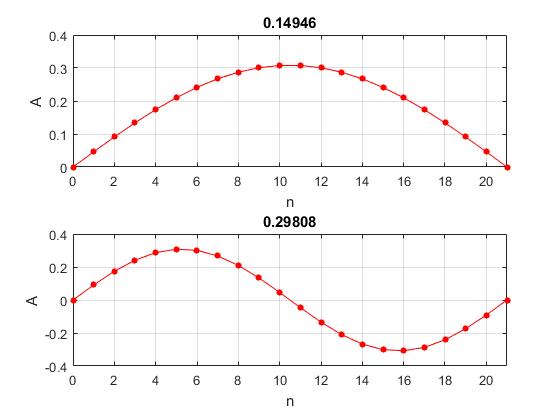
Se representan los dos primeros modos de vibración para un sistema de N=20 partículas

Amortiguamiento

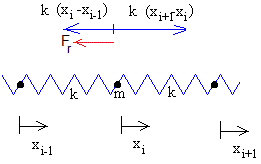
A la ecuación diferencial que describe el movimiento de la partícula i, estudiada al principio de esta página, añadimos un término que corresponde a una fuerza de rozamiento F_r=λdx_i/dt proporcional a la velocidad de la partícula i, (véase las oscilaciones amortiguadas)

${\displaystyle \begin{array}{l}m\frac{d^2{x}_i}{d{t}^2}=-\lambda \frac{d{x}_i}{dt}-k(x_i-x_{i-1})+k(x_{i+1}-x_i)\hfill \\ \frac{d^2{x}_i}{d{t}^2}+2\gamma \frac{d{x}_i}{dt}+{\omega }_0^2\left(2x_i-x_{i-1}-x_{i+1}\right)=0\hfill \end{array}}$

donde ${\omega }_0^2=\frac{k}{m},2\gamma =\frac{\lambda }{m}$. Probamos una solución de la forma

${\displaystyle x_i(t)=A_i\exp (-\gamma t)\cos (\omega t)}$

Calculamos la derivada primera y segunda de x_i

${\displaystyle \begin{array}{l}\frac{d{x}_i}{dt}=-\exp (-\gamma t)A_i\left(\gamma \cos (\omega t)+\omega \sin (\omega t)\right)\\ \frac{d^2{x}_i}{d{t}^2}=-\exp (-\gamma t)A_i\left\{\left({\gamma }^2-{\omega }^2\right)\cos (\omega t)+2\gamma \omega \sin (\omega t)\right\}\end{array}}$

El resultado es la relación de recurrencia que hemos estudiado al principo de esta página, pero con otra expresión para la variable s

${\displaystyle \begin{array}{l}-\left({\omega }^2+{\gamma }^2\right)A_i+{\omega }_0^2\left(2A_i-A_{i-1}-A_{i+1}\right)=0\\ A_{i+1}-2s{A}_i+A_{i-1}=\mathrm{0,}s=\frac{2{\omega }_0^2-{\omega }^2-{\gamma }^2}{2{\omega }_0^2}\end{array}}$

con i=1,2,3...N, siendo N el número de partículas de masa m unidas a N+1 muelles elásticos de constante k. Los extremos x₀=0 y x_N+1=0 están fijos por lo que A₀=0 y A_N+1=0 que equivale a la ecuación U_N(s)=0, tal como se ha explicado en el primer apartado.

Las frecuencias ω_n están relacionadas con las raíces s_n del polinomio U_N(s)=0 de Chebyshev.

${\displaystyle \begin{array}{l}{s}_n=\cos \left(\frac{n\pi }{N+1}\right)n=\mathrm{1,2,...}N\\ {\omega }_n^2=2{\omega }_0^2\left(1-\cos \left(\frac{n\pi }{N+1}\right)\right)-{\gamma }^2\\ {\omega }_n^2=4{\omega }_0^2{\sin }^2\left(\frac{n\pi }{2(N+1)}\right)-{\gamma }^2\end{array}}$

Calculamos las amplitudes A_i de la partícula i, tal como se hizo en el apartado, titulado Amplitudes. La posición x_i de la partícula i en función del tiempo t, suponiendo oscilaciones amortiguadas, es

${\displaystyle x_i(t)=A_0\frac{\sin \left(i·\frac{n\pi }{N+1}\right)}{\sin \left(\frac{n\pi }{N+1}\right)}\exp \left(-\gamma t\right)\cos \left({\omega }_{n}t\right)}$

Siempre que la constante de amortiguamiento γ no sea muy grande, de modo que ω_n sea un número real, estaríamos entonces en el caso de oscilaciones amortiguadas, si fuera complejo, daría lugar a oscilaciones sobreamortiguadas

Actividades

Se ha fijado

• La masa de las partículas, m=1 kg
• La constante elástica de los muelles, k=1 N/m

Se introduce

• El número N de partículas, en el control titulado Número de partículas
• La constante γ de amortiguamiento, en el control titulado Amortiguamiento

Se pulsa el botón titulado Nuevo

Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular.

Se pulsa el botón titulado >>, observamos los siguientes modos normales

Se pulsa el botón titulado << para observar el modo normal de vibración anterior.

En la parte inferior, se muestra el desplazamiento de las partículas

Relación de dispersión, N=∞

Cadena monoatómica

En la ecuación diferencial

${\displaystyle m\frac{d^2{x}_i}{d{t}^2}=k{x}_{i-1}-2k{x}_i+k{x}_{i+1}}$

Probamos una solución de la forma

${\displaystyle \begin{array}{l}{x}_i=A_i\cos \left(\omega t\right),A_i=A\sin \left(K·ia\right)\\ \begin{array}{l}-m{\omega }^2\sin \left(Kia\right)=k\sin \left(K(i-1)a\right)-2k\sin \left(Kia\right)+kin\left(K(i+1)a\right)\hfill \\ \begin{array}{l}\sin \left(K(i+1)a\right)+\sin \left(K(i-1)a\right)-2\left(1-\frac{m}{2k}{\omega }^2\right)\sin (Kia)=0\\ 2\sin (Kia)\cos (Ka)-2\left(1-\frac{m}{2k}{\omega }^2\right)\sin (Kia)=0\end{array}\hfill \end{array}\end{array}}$

donde K es el número de onda K=2π/λ. Simplificando

${\displaystyle \begin{array}{l}\cos (Ka)=1-\frac{m}{2k}{\omega }^2\hfill \\ {\omega }^2=4\frac{k}{m}{\sin }^2\left(\frac{Ka}{2}\right)\hfill \end{array}}$

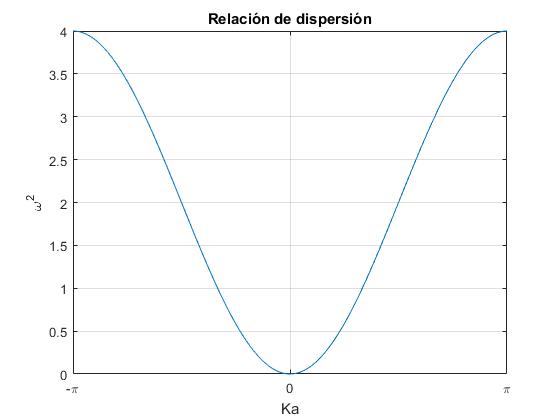
Esta ecuación que relaciona la frecuencia angular ω con el número de onda K, se denomina relación de dispersión.

En la figura, se representa el cuadrado de la frecuencia angular ω en función de Ka (donde K es el número de onda) en el intervalo (-π, +π).

fplot('4*sin(x/2)^2',[-pi,pi])
set(gca,'XTick',(-1:1)*pi)
set(gca,'XTickLabel',{'-\pi','0','\pi'})
xlabel('Ka')
ylabel('\omega^2')
grid on
title('Relación de dispersión')

Cadena diatómica

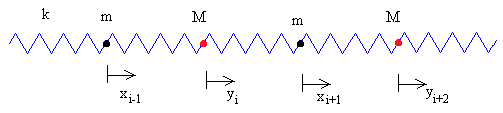
Consideremos una cadena lineal de moléculas diatómicas separados una distancia a en la situación de equilibrio, tal como se muestra en la figura.

Consideremos el movimiento de dos átomos contiguos.

• El desplazamiento del átomo i de masa M denominamos y_i
• El desplazamiento del átomo i+1 de masa m denominamos x_i+1

Ecuaciones del movimiento

${\displaystyle \begin{array}{l}M\frac{d^2{y}_i}{d{t}^2}=-k(y_i-x_{i-1})+k(x_{i+1}-y_i)\\ m\frac{d^2{x}_{i+1}}{d{t}^2}=-k(x_{i+1}-y_i)+k(y_{i+2}-x_{i+1})\end{array}}$

Probamos una solución de la forma

y_i=A_icos(ωt), con A_i=Asin(Kia)

x_i+1=A_i+1cos(ωt), con A_i+1=Bsin(K(i+1)a)

donde K se denomina número de onda

Introducimos estas soluciones en las dos ecuaciones diferenciales y obtenemos un sistema homogéneo de dos ecuaciones con dos incógnitas A y B.

A(-ω²M+2k)sin(Kia)-Bk(sin(K(i+1)a)+sin(K(i-1)a))=0
-Ak(sin(K(i+2)a)+sin(Kia))+B(-ω²m+2k) sin(K(i+1)a)=0

Teniendo en cuenta que

sin(K(i+1)a)+sin(K(i-1)a)=2sin(Kia)cos(Ka)
sin(K(i+2)a)+sin(Kia)= 2sin(K (i+1)a)cos(Ka)

y eliminamos A y B en el sistema homogéneo de dos ecuaciones

(-ω²M+2k) (-ω²m+2k)sen(Kia)sen(K(i+1)a)-4k²sen(Kia)cos²(Ka)sen(K(i+1)a))=0

Simplificando el factor común sin(Kia)sin(K(i+1)a)

${\displaystyle \begin{array}{l}{\omega }^4-2k\frac{m+M}{mM}+4\frac{k^2}{mM}{\sin }^2(Ka)=0\\ {\omega }^2=k\left(\frac{1}{M}+\frac{1}{m}\right)\pm k\sqrt{\left({\left(\frac{1}{M}+\frac{1}{m}\right)}^2-4\frac{{\sin }^2(Ka)}{mM}\right)}\end{array}}$

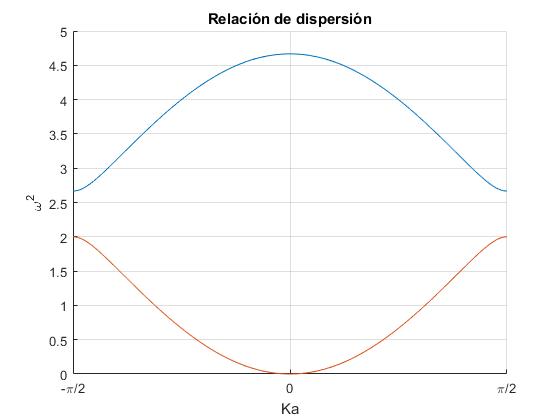
Esta ecuación que relaciona la frecuencia ω con el número de onda K, se denomina relación de dispersión.

En la figura, se representa se representa el cuadrado de la la frecuencia angular ω en función Ka (donde K es del número de onda) en el intervalo (-π/2, +π/2). La curva superior (signo +) se denomina rama óptica, y la inferior (signo -) se denomina rama acústica.

M=0.75;
m=1;
k=1;
f1=@(x) k*(1/m+1/M)+k*sqrt((1/m+1/M)^2-4*sin(x)^2/(m*M));
f2=@(x) k*(1/m+1/M)-k*sqrt((1/m+1/M)^2-4*sin(x)^2/(m*M));
hold on
fplot(f1,[-pi/2,pi/2])
fplot(f2,[-pi/2,pi/2])
hold off
set(gca,'XTick',(-1:1)*pi/2)
set(gca,'XTickLabel',{'-\pi/2','0','\pi/2'})
xlabel('Ka')
ylabel('\omega^2')
grid on
title('Relación de dispersión')

Referencias

Runk R. B. Stul J. L. Anderson G. L. A laboratory analog for lattice dynamics. Am. J. Phys. (31) 1963, pp. 915-921

John H. Van Drie, Jr., Peter W. Murphy. Chebyshev polynomials in the loaded-string problem. American Journal of Physics Vol. 43, No. 4, April 1975, pp. 361-362

N Gauthier. Exact expressions for the amplitudes and damped normal frequencies of taut vibrating linear string of couped masses. Eur. J. Phys. 29 (2008) N21-N29