Resonancias y antiresonancias.
Oscilaciones forzadas en un sistema formado por partículas unidas por muelles
La solución particular del sistema de ecuaciones diferenciales indica que cada partícula describirá un MAS de amplitud A y frecuencia angular ωf, en fase o en oposición de fase con la fuerza oscilante. Representaremos la amplitud A en función de la frecuencia de la fuerza oscilante ωf para identificar las resonancias y antiresonancias.
Sistema de dos partículas, N=2
Consideremos un sistema formado por dos partículas unidas por muelles elásticos.
Las ecuaciones diferenciales del movimiento de cada una de las partículas es
Nos fijamos que con esta notación, la matriz M de las masas es la matriz unidad. Por lo que calculamos los valores propios y los vectores propios de la matriz K, cuyos términos son proporcionales al cociente k/m. Los pasos para obtener la representación gráfica de las amplitudes de cada una de las partículas en función de la frecuencia de la fuerza oscilante ω son los siguientes:
1.-Valores propios de la matriz K. Frecuencias de los modos normales de vibración
>> syms w0;
>> K=sym('[2*w0^2,-w0^2;-w0^2,2*w0^2]');
>> [V,D]=eig(K)
V =
[ -1, 1]
[ 1, 1]
D =
[ 3*w0^2, 0]
[ 0, w0^2]
La matriz diagonal D contiene en su diagonal principal los cuadrados de las frecuencias de los modos normales de vibración, ω1 y ω2.
Los vectores columna de la matriz V son los vectores propios correspondientes a cada uno de los valores propios.
2.-Cálculo de la matriz V. Las ecuaciones diferenciales del movimiento se desacoplan
Creamos una nueva matriz V, multiplicando los vectores propios por un factor de escala de modo que
>> M=[1,0;0,1]; >> X1=V(:,1); >> X2=V(:,2); >> r=X1'*M*X1 r =2 >> X1=X1/sqrt(r); >> r=X2'*M*X2 r =2 >> X2=X2/sqrt(r); >> V=[X1,X2]; >> Mg=V'*M*V Mg = [ 1, 0] [ 0, 1] >> Kg=V'*K*V Kg = [ 3*w0^2, 0] [ 0, w0^2]
La nueva matriz V es
Definimos un nuevo vector u(t) de modo que
La ecuación diferencial del movimiento en forma matricial se transforma en
3.-Solución de las ecuaciones diferenciales del movimiento desacopladas
El comportamiento del sistema se describe mediante un sistema de dos ecuaciones diferenciales desacopladas
La solución de cada una de estas ecuaciones diferenciales es la suma de su homogénea que depende de las condiciones iniciales y de la solución particular que depende de la expresión de cada una de las fuerzas f1(t) y f2(t). Supondremos que se ha alcanzado el estado estacionario, por lo que solamente estamos interesados en la solución particular.
>> syms t w f0; >> F=[f0*cos(w*t);0]; >> f=V'*F f = -(2^(1/2)*f0*cos(t*w))/2 (2^(1/2)*f0*cos(t*w))/2
Las soluciones particulares u1(t) y u2(t) de las ecuaciones diferenciales del movimiento desacopladas se puede calcular fácilmente.Véase el oscilador forzado sin rozamiento γ=0
- u1(t)=A1cos(ωt)
- u2(t)=A2cos(ωt)
Calculamos A1y A2 introduciendo cada solución particular en su ecuación diferencial respectiva.
4.-Posición de cada una de las partículas en función del tiempo
Una vez que obtenemos el movimiento de cada partícula en términos de las coordendas u1(t) y u2(t) se vuelven a transformar en coordenadas físicas x1(t) y x2(t), mediante x=V·u.
>> u=f./(diag(D)-w^2); >> x=V*u u = (2^(1/2)*f0*cos(t*w))/(2*(w^2 - 3*w0^2)) -(2^(1/2)*f0*cos(t*w))/(2*(w^2 - w0^2)) x = - (f0*cos(t*w))/(2*(w^2 - w0^2)) - (f0*cos(t*w))/(2*(w^2 - 3*w0^2)) (f0*cos(t*w))/(2*(w^2 - 3*w0^2)) - (f0*cos(t*w))/(2*(w^2 - w0^2))
5.-Representación gráfica de las amplitudes de cada MAS en función de la frecuencia ω
Los coeficientes B1 y B2 que multiplican a cos(ωt) en las expresiones de x1(t) y x2(t) son las amplitudes que vamos a representar en función de la frecuencia ω/ω0 de la fuerza oscilante.
- x1(t)=B1cos(ωt)
- x2(t)=B2cos(ωt)
>> B=x/(f0*cos(w*t))
>> B= simplify(B)
B =
- 1/(2*(w^2 - w0^2)) - 1/(2*(w^2 - 3*w0^2))
1/(2*(w^2 - 3*w0^2)) - 1/(2*(w^2 - w0^2))
>> B=subs(B,w0,sym('1'))
B =
- 1/(2*(w^2 - 1)) - 1/(2*(w^2 - 3))
1/(2*(w^2 - 3)) - 1/(2*(w^2 - 1))
>> hold on
>> ezplot(B(1),[0,3])
>> hg=ezplot(B(2),[0,3]);
>> set(hg,'color','r')
>> hold off
>> grid on
>> xlabel('\omega/\omega_0')
>> ylabel('Amplitud')
>>title('Dos osciladores acoplados, forzados')
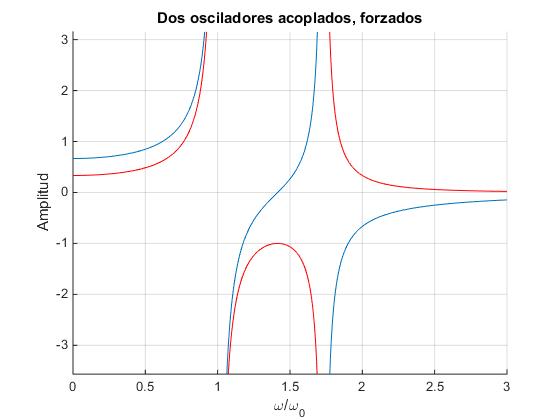
La amplitud B1se hace cero cuando
A esta frecuencia se le denomina antiresonancia ωa.
B2 presenta un máximo para esta misma frecuencia, como puede probarse calculando la derivada respecto de ω e igualando a cero.
En un MAS, las amplitudes se consideran cantidades positivas por lo que la ecuación del movimiento de cada partícula se escribe
- x1(t)=|B1|cos(ωt+δ1)
- x2(t)=|B2|cos(ωt+δ2)
- Una amplitud negativa equivale a una amplitud positiva con una fase inicial δ=π. El desplazamiento x de la partícula está en oposición de fase con la fuerza oscilante.
- Una amplitud positiva equivale a una amplitud positiva con una fase inicial δ=0. El desplazamiento x de la partícula está en fase a la fuerza oscilante.
En la figura vemos que
- De ω=0 a ω=ω1: las amplitudes B1 y B2 son positivas y las fases δ1=0 y δ2=0.
- De ω=ω1 a ω=ωa: las amplitudes B1 y B2 son negativas y las fases δ1=π y δ2=π.
- De ω=ωa a ω=ω2: la amplitudes B1 es positiva y B2 es negativa y las fases δ1=0 y δ2=π.
- De ω=ω2 a ω=∞ la amplitud B1 es negativa y B2 es positiva y las fases δ1=π y δ2=0.
>> hold on >> ezplot(abs(B(1)),[0,3]) >> hg=ezplot(abs(B(2)),[0,3]); >> set(hg,'color','r') >> hold off >> grid on
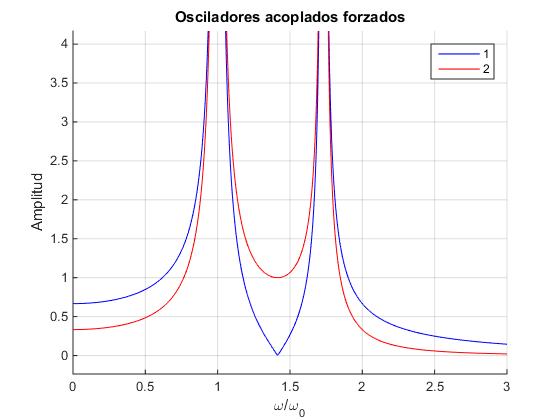
Unimos las distintas porciones de código para crear un script que pueda ser modificado para estudiar otros sistemas, por ejemplo cinco partículas de masa m unidas a muelles elásticos iguales de constante k.
syms w0 t w f0;
K=sym('[2*w0^2,-w0^2;-w0^2,2*w0^2]');
M=sym('[1,0;0,1]');
F=[f0*cos(w*t);0];
[V,D]=eig(K);
for k=1:length(F)
X=V(:,k);
r=X'*M*X;
X=X/sqrt(r);
V(:,k)=X;
end
f=V'*F;
u=f./(diag(D)-w^2);
x=V*u;
B=x/(f0*cos(w*t));
B=simplify(B);
B=subs(B,w0,sym('1'))
color=['b','r','g','k','c'];
hold on
for k=1:length(F)
hg=ezplot(abs(B(k)),[0,3]);
set(hg,'color',color(k),'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','NorthEast')
xlabel('\omega/\omega_0')
ylabel('Amplitud')
title('Osciladores acoplados forzados')
Sistema de cinco partículas, N=5
Escribimos las ecuaciones del movimiento de cada una de las partículas y su representación matricial
Utilizamos el mismo script que para dos partículas, solamente tenemos que cambiar la matriz K, la matriz M y el vector F, el resto del código no cambia
syms w0 t w f0;
K=sym('[2*w0^2,-w0^2,0,0,0;-w0^2,2*w0^2,-w0^2,0,0;0,-w0^2,2*w0^2,...
-w0^2,0;0,0,-w0^2,2*w0^2,-w0^2;0,0,0,-w0^2,2*w0^2]');
M=sym('[1,0,0,0,0;0,1,0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1]');
F=[f0*cos(w*t);0;0;0;0];
......
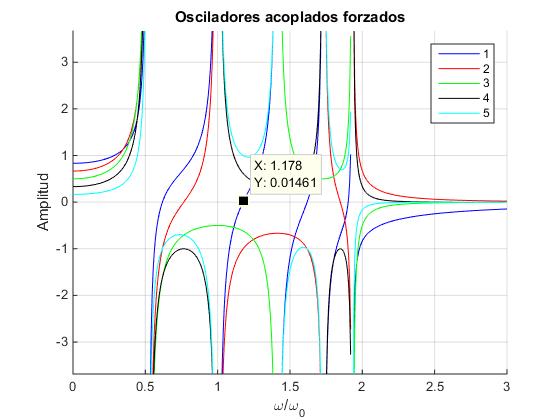
En esta gráfica observamos que las amplitudes se hacen muy grandes, tienden a infinito, cuando la frecuencia ω de la fuerza oscilante se hace igual a la frecuencia de cada uno de los modos normales de vibración ωi, i=1,2,3,4,5. Los cuadrados de estas frecuencias están en la diagonal de la matriz D de los valores propios de la matriz K.
>> w2=diag(D);
w2 =
2*w0^2
w0^2
3*w0^2
3^(1/2)*w0^2 + 2*w0^2
2*w0^2 - 3^(1/2)*w0^2
>> w2=subs(w2,w0,sym('1'))
w2 =
2
1
3
3^(1/2) + 2
2 - 3^(1/2)
>> double(sqrt(w2))
ans =
1.0000
1.4142
1.7321
1.9319
0.5176
Las amplitudes se hacen nulas para ciertas frecuencias denominadas antiresonancias. Utilizando el icono Data Cursor de la ventana gráfica vemos los valores aproximados de las frecuencias. Alternativamente, la función solve de Math Symbolic nos calcula las raíces. Buscamos los ceros de la primera amplitud B1 (solamente son válidos los valores positivos)
>> wa=solve(B(1))
wa =
5^(1/2)/2 + 1/2
1/2 - 5^(1/2)/2
5^(1/2)/2 - 1/2
- 5^(1/2)/2 - 1/2
(5^(1/2)/2 + 5/2)^(1/2)
(5/2 - 5^(1/2)/2)^(1/2)
-(5^(1/2)/2 + 5/2)^(1/2)
-(5/2 - 5^(1/2)/2)^(1/2)
>> double(wa)
ans =
1.6180
-0.6180
0.6180
-1.6180
1.9021
1.1756
-1.9021
-1.1756
Buscamos los ceros de la segunda amplitud B2
>> wa=solve(B(2))
wa =
(2^(1/2) + 2)^(1/2)
-(2^(1/2) + 2)^(1/2)
(2 - 2^(1/2))^(1/2)
-(2 - 2^(1/2))^(1/2)
>> double(wa)
ans =
1.8478
-1.8478
0.7654
-0.7654
La tercera amplitud B3 y la cuarta B4 no tienen ceros
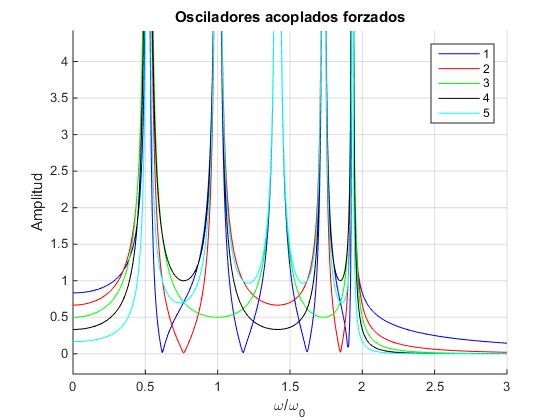
En la gráfica anterior vemos también los intervalos en los que cada una de las cinco amplitudes cambia de signo, lo que nos permite determinar la fase (en fase o en oposición de fase a la fuerza oscilante). Los valores absolutos de las amplitudes se representan en la siguiente gráfica
Cuando hay rozamiento
Vamos a mostrar con un ejemplo que cuando hay rozamiento proporcional a la velocidad la antiresonancia no está presente.
Para un sistema de dos partículas las ecuaciones del movimiento son ahora.
Si combinamos las dos ecuaciones diferenciales primero sumando y luego restando, obtenemos dos ecuaciones diferenciales del movimiento desacopladas en términos de dos nuevas variables X1=x1+x2 y X2=x1-x2.
Las soluciones particulares de estas dos ecuaciones diferenciales se obtienen introduciendo en cada una de ellas X=Acos(ωt)+Bsin(ωt). Calculamos los coeficientes A1,B1, A2 B2.
Las soluciones de las dos ecuaciones diferenciales desacopladas son
Los desplazamientos x1 y x2 de las partículas en función del tiempo son:
Representamos C1 y C2 en función del cociente de la frecuencia de la fuerza oscilante ω/ω0
w=linspace(0,2.5,200);
w0=1;
f0=1;
g=0.1;
A1=(w0^2-w.^2)./((w0^2-w.^2).^2+4*g^2*w.^2);
B1=2*g*w./((w0^2-w.^2).^2+4*g^2*w.^2);
A2=(3*w0^2-w.^2)./((3*w0^2-w.^2).^2+4*g^2*w.^2);
B2=2*g*w./((3*w0^2-w.^2).^2+4*g^2*w.^2);
C1=sqrt((A1+A2).^2+(B1+B2).^2)/2;
C2=sqrt((A1-A2).^2+(B1-B2).^2)/2;
hold on
plot(w,C1,'b')
plot(w,C2,'r')
hold off
grid on
legend('1','2');
xlabel('\omega/\omega_0')
ylabel('Amplitud')
title('Osciladores acoplados, forzados con rozamiento')
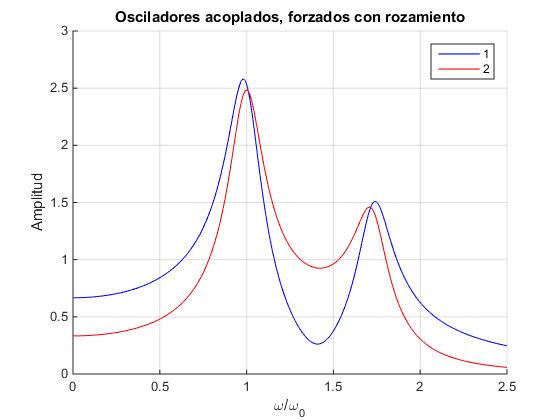
Como vemos en la figura, C1 y C2 ya no se hacen cero. No hay antiresonancias.
Referencias
Somayyeh Belbasi, M. Ebrahim Foulaadvand, Young S. Joe. Anti-resonance in one-dimensional chain of driven coupled oscillators. Am. J. Phys. 82 (1) January 2014. pp. 32-38

