Oscilaciones acopladas de una varilla que pende de dos muelles
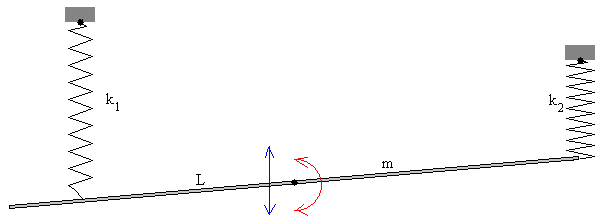
Equilibrio
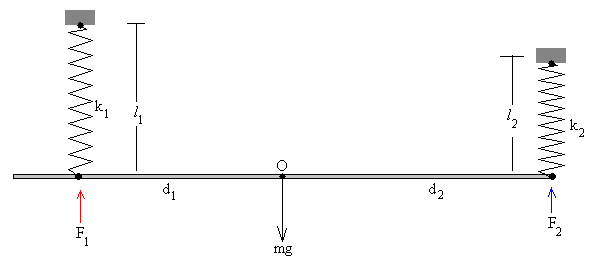
La varilla delgada de masa m kg y longitud L pende de dos muelles elásticos verticales de constantes k1 y k2 y de longitudes l01 y l02 sin deformar, situados a una distancia d1 y d2 a uno y otro lado del c.m de la varilla
-
La fuerza que ejerce el muelle situado a la izquierda del c.m. es F1=k1x1, donde x1 es la deformación del muelle
-
La fuerza que ejerce el muelle situado a la derecha del c.m. es F2=k2x2, donde x2 es la deformación del muelle
Cuando la varilla está en equilibrio en posición horizontal. La resultante de las fuerzas sobre la varilla debe ser cero y el momento resultante respecto del c.m. debe ser cero.
k1x1+ k2x2=mg
-k1x1·d1+ k2x2·d2=0
Despejamos x1 y x2
-
El muelle de la izquierda se ha de colgar de un punto situado a l1=l01+x1 por encima de la varilla horizontal
-
El muelle de la derecha se ha de colgar de un punto situado a l2=l02+x2 por encima de la varilla horizontal
Ecuaciones del movimiento
Supondremos que el sistema realiza pequeños desplazamientos respecto de la posición de equilibrio para que las ecuaciones del movimiento sean lineales.
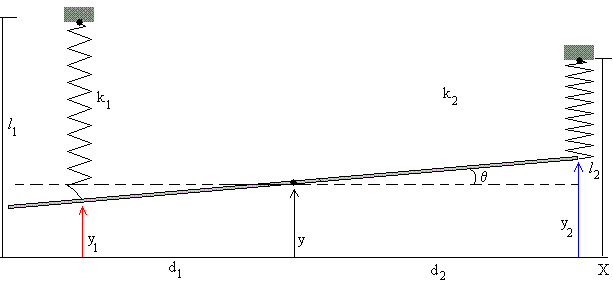
Supongamos que en el instante t, el c.m. de la varilla se ha elevado y sobre la posición de equilibrio y ha girado un ángulo θ, respecto de la posición horizontal.
-
La deformación del muelle izquierdo es l1-l01-y1= x1-y1, y la fuerza que ejerce el muelle izquierdo sobre la varilla es F1=k1(x1-y1)
-
La deformación del muelle derecho es l2-l02-y2= x2-y2, y la fuerza que ejerce el muelle derecho sobre la varilla es F2=k2(x2-y2)
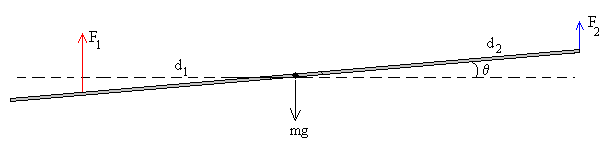
La ecuación del movimiento de traslación del c.m es
La ecuación del movimiento de rotación alrededor de un eje perpendicular a la varilla y que pasa por el c.m. es
Ic=mL2/12 es el momento de inercia de la varilla de longitud L respecto de un eje perpendicular a la varilla y que pasa por el c.m.
Relacionamos los desplazamientos y1 e y2 de los puntos de enganche de los muelles con la varilla con el desplazamiento y del c.m. y con el ángulo θ girado por la varilla que supondremos de nuevo, que es pequeño, para que las ecuaciones del movimiento sean lineales
y1=y-d1·θ
y2=y+d2·θ
Las dos ecuaciones diferenciales del movimiento las escribimos en términos del desplazamiento y del c.m. y del ángulo girado θ por la varilla.
Definimos los siguientes parámetros
Las dos ecuaciones se escriben en términos de dichos parámetros, del siguiente modo
Para eliminar el ángulo θ, calculamos la derivada segunda de la primera ecuación diferencial
que con las otras dos, da lugar la ecuación diferencial de cuarto orden en y
Ensayamos una solución de la forma
y=Asin(ωt)+Bcos(ωt) o bien, y=Csin(ωt+φ)
Calculamos la derivada segunda y la derivada cuarta de y y las introducimos en la ecuación diferencial de cuarto orden, obteniendo la siguiente ecuación bicuadrada en ω.
cuyas raíces reales son
La forma general del desplazamiento y en función del tiempo t es una combinación lineal de los dos modos normales de vibración
y (t)=Asin(ω1t)+Bcos(ω1t)+Csin(ω2t)+Dcos(ω2t)
La velocidad del c.m. es
Para calcular el ángulo θ(t) girado por la varilla en función del tiempo, se introduce y(t) y su derivada segunda en la ecuación diferencial de segundo orden que describe el movimiento del c.m. de la varilla
resultando
La velocidad de rotación de la varilla es
Las condiciones iniciales determinan los valores de los coeficientes A, B, C, D.
Desplazamos el c.m. de la varilla y0 y la giramos un ángulo θ0 y a continuación, la soltamos. La velocidad inicial es dy/dt=0, dθ/dt=0 en el instante t=0.
Tenemos que resolver el sistema de cuatro ecuaciones
Despejamos A, B, C, y D
A=C=0
Las expresiones de la posición y y θ y velocidad dy/dt y dθ/dt en función del tiempo son
y(t)= Bcos(ω1t)+ Dcos (ω2t)
m=1; %masa de la varilla
L=2; %longitud d ela varilla
k1=30; %constante del primer muelle
k2=25; %constante del segundo muelle
d1=-0.577; %posición del primer muelle (frecuencias iguales)
d2=0.577; %posición del segundo muelle
y0=0; %altura inicial del c.m.
fi0=5*pi/180; %ángulo inicial de giro de la varilla
wy=(k1+k2)/m; %cuadrado de
wfi=(k1*d1^2+k2*d2^2)/(m*L^2/12); %cuadrado de
beta=k2*d2+k1*d1;
w1=(wfi+wy)/2+sqrt((wfi-wy)^2+4*beta^2/(m*m*L^2/12))/2;
w2=(wfi+wy)/2-sqrt((wfi-wy)^2+4*beta^2/(m*m*L^2/12))/2;
D=(beta*fi0/m-(w1-wy)*y0)/(w2-w1);
B=(-beta*fi0/m+(w2-wy)*y0)/(w2-w1);
t=linspace(0,20,400);
ang=(m/beta)*((w1-wy)*B*cos(sqrt(w1)*t)+(w2-wy)*D*cos(sqrt(w2)*t));
y=B*cos(sqrt(w1)*t)+D*cos(sqrt(w2)*t);
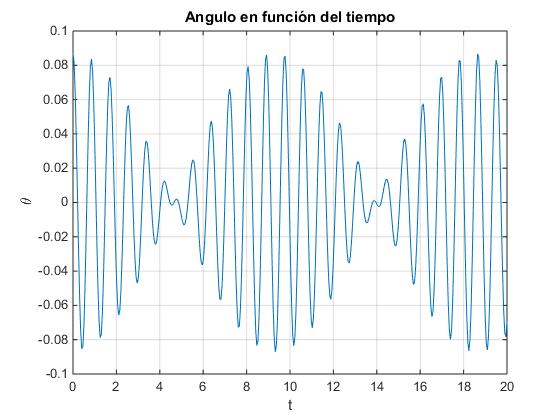
plot(t,ang)
grid on
xlabel('t')
ylabel('\theta')
title('Angulo en función del tiempo')
figure
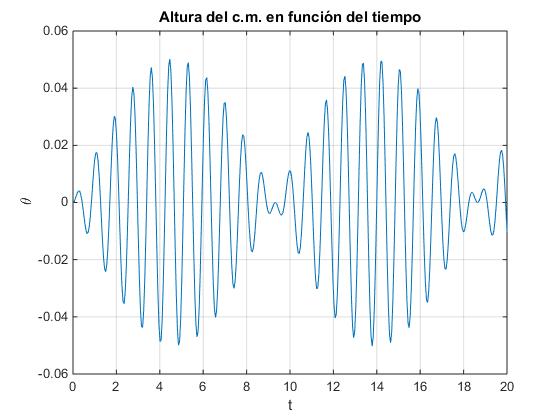
plot(t,y)
grid on
xlabel('t')
ylabel('\theta')
title('Altura del c.m. en función del tiempo')
Modos normales de vibración
-
El modo 1 de frecuencia angular ω1, se obtiene cuando D=0
-
El modo 2 de frecuencia angular ω2, se obtiene cuando B=0,
La relación entre la posición inicial y0 del c.m. de la varilla y el ángulo inicial de giro θ0 es
B=y0
La posición y del c.m. de la varilla y el ángulo girado θ en función del tiempo t son
y(t)= y0cos(ω1t)
La relación entre la posición inicial y0 del c.m. de la varilla y el ángulo inicial de giro θ0 es
D=y0
La posición y del c.m. de la varilla y el ángulo girado θ en función del tiempo t son
Oscilaciones no acopladas
Cuando β=0 las oscilaciones no están acopladas, se debe cumplir para ello que
k1·d1=k2·d2
Las ecuaciones del movimiento del c.m. de la varilla y de la rotación de la varilla alrededor de un eje que pasa por el c.m. son
y=A1sin(ωyt)+B1cos(ωyt)
θ=A2sin(ωθt)+B2cos(ωθt)
las constantes A1, B1, A2, B2 se determinan a partir de las condiciones iniciales: en el instante t=0, y=y0, dy/dt=0, θ=θ0, dθ/dt=0
y=y0cos(ωyt)
θ=θ0cos(ωθt)
Obtenemos este mismo resultado, a partir de las soluciones del sistema de dos ecuaciones diferenciales con las condiciones iniciales especificadas, al final del apartado “Ecuaciones del movimiento”
Cuando β→0, ω1→ωy, y ω2→ωθ, los coeficientes D→0, B→y0
El movimiento del c.m. de la varilla es un MAS de frecuencia angular ωy.
y=y0cos(ωyt)
Algo más complicado es obtener la ecuación del movimiento de rotación θ(t). Los coeficientes de cos(ω1t) y de cos(ω2t) valen respectivamente
La rotación de la varilla alrededor de un eje que pasa por el c.m. es un MAS de frecuencias ωθ
θ=θ0cos(ωθt)
Frecuencias iguales
Para que las frecuencias angulares sean iguales ωy=ωθ=ω se debe cumplir que
Como Ic=mL2/12, se cumple esta igualdad si
siendo L la longitud de la varilla
Las frecuencias ω1 y ω2 de los modos normales de vibración tienen una expresión mucho más simple
Es importante analizar el caso de que θ0=0. Se desplaza la varilla hacia arriba o hacia abajo horizontalmente y0 y luego, se suelta.
Los coeficientes B=D=y0/2. El movimiento del c.m. de la varilla y la rotación de la varilla se describen mediante las ecuaciones
-
La relación entre la posición inicial y0 del c.m. y el ángulo inicial de giro θ0 es en el modo normal 1 de frecuencia angular ω1 es
-
La relación entre la posición inicial y0 del c.m. y el ángulo inicial de giro θ0 es en el modo normal 2 de frecuencia angular ω2 es
Balance energético
La energía del sistema está compuesta por los siguientes términos (véase la primera figura de esta página):
-
La energía cinética de traslación del c.m. de la varilla
-
La energía cinética de rotación de la varilla alrededor de un eje perpendicular a la varilla y que pasa por el c.m.
-
El muelle de la izquierda está deformado (x1-y1)=(x1-y+d1·θ). La energía potencial acumulada en el muelle deformado de constante k1 es
-
El muelle de la derecha está deformado (x2-y2)=(x2-y-d2·θ). La energía potencial acumulada en el muelle deformado de constante k2 es .
x1 y x2 son las deformaciones de los muelles cuando soportan la varilla horizontal y en reposo. -
El centro de masa se encuentra a una altura y sobre la posición de equilibrio, la energía potencial es mgy.
Como el sistema es conservativo, la suma de todas estas energías es constante.
Actividades
Se introduce
-
La constante elástica k1 del muelle de la izquierda en N/m, en el control titulado Constante k1.
-
La constante elástica k2 del muelle de la derecha en N/m, en el control de titulado Constante k2.
-
Se establece la posición de enganche de los muelles a la varilla, es decir las distancias d1 y d2 de los muelles al c.m. en los controles Posición 1 y Posición 2, respectivamente
-
Se establece la posición inicial y0 del c.m. de la varilla, en el control titulado Altura c.m.
-
Se establece el ángulo inicial θ0 de giro de la varilla en grados, en el control titulado Angulo
-
La masa de la varilla se ha fijado en m=1 kg
-
La longitud de la varilla se ha fijado en L=2 m
Se pulsa el botón titulado Nuevo.
En la parte superior derecha, se proporciona el valor de la energía total del sistema, que deberá permanecer constante.
Referencias
Karioris F. G., Mendelson K. S., A novel coupled oscillation demostration. Am. J. Phys. 60 (6) June 1992, pp. 508-513

