Ecuaciones del movimiento

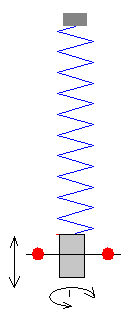
Sea k_x la constante elástica del muelle en las oscilaciones longitudinales y k_θ a constante en las oscilaciones torsionales. Sea x el desplazamiento vertical del muelle de la posición de equilibrio y θ el ángulo de rotación alrededor del eje vertical.

El acoplamiento entre los dos modos de oscilación está descrito por una función lineal de la forma εxθ /2, donde ε se denomina constante de acoplamiento.

La energía del sistema es la suma de la energía cinética de traslación del bloque, de rotación alrededor del eje vertical, la energía potencial del muelle cuando se deforma una longitud x, cuando gira un ángulo θ y la energía de acoplamiento

${\displaystyle E=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}I{\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}{k}_x{x}^2+\frac{1}{2}{k}_{\theta }{\theta }^2+\frac{1}{2}\epsilon x\theta }$

Las ecuaciones del movimiento de Lagrange nos llevan al sistema de dos ecuaciones diferenciales de segundo orden. La lagrangiana L=T-V con los símbolos $\dot{\theta }=\frac{d\theta }{dt}\dot{x}=\frac{dx}{dt}$ se escribe

${\displaystyle \begin{array}{l}L=\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}I{\dot{\theta }}^2-\frac{1}{2}{k}_x{x}^2-\frac{1}{2}{k}_{\theta }{\theta }^2-\frac{1}{2}\epsilon x\theta \\ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}}-\frac{\partial L}{\partial x}=0\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }}-\frac{\partial L}{\partial \theta }=0\end{array}}$

Las ecuaciones del movimiento son:

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+\frac{k_x}{m}x+\frac{\epsilon }{2m}\theta =0\\ \frac{d^2\theta }{d{t}^2}+\frac{k_{\theta }}{I}\theta +\frac{\epsilon }{2I}x=0\end{array}}$

En ausencia del término de acoplamiento ε=0 las ecuaciones diferenciales describen dos Movimientos Armónicos Simples de frecuencias angulares

${\displaystyle {\omega }_x^2=\frac{k_x}{m}{\omega }_{\theta }^2=\frac{k_{\theta }}{I}}$

Eliminamos x en el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^4\theta }{d{t}^4}+{\omega }_{\theta }^2\left(\frac{d^2\theta }{d{t}^2}\right)+\frac{\epsilon }{2I}\left(\frac{d^{2}x}{d{t}^2}\right)=\\ \frac{d^4\theta }{d{t}^4}+{\omega }_{\theta }^2\left(\frac{d^2\theta }{d{t}^2}\right)+\frac{\epsilon }{2I}\left(-{\omega }_x^{2}x-\frac{\epsilon }{2m}\theta \right)=0\\ \frac{d^4\theta }{d{t}^4}+({\omega }_{\theta }^2+{\omega }_x^2)\left(\frac{d^2\theta }{d{t}^2}\right)+\left({\omega }_{\theta }^2·{\omega }_x^2-\frac{{\epsilon }^2}{4mI}\right)\theta =0\end{array}}$

Suponiendo una solución de la forma

θ=A·sin(ωt)+ B·cos(ωt)

e insertándola en la ecuación diferencial de cuarto orden en θ, obtenemos la ecuación bicuadrada

${\displaystyle {\omega }^4-{\omega }^2({\omega }_x^2+{\omega }_{\theta }^2)+{\omega }_x^2·{\omega }_{\theta }^2-\frac{{\epsilon }^2}{4mI}=0}$

Las dos raíces reales de esta ecuación son las frecuencias ω₁ y ω₂ de los modos normales de vibración

$$\begin{gathered} {\displaystyle \begin{array}{l}{\omega }_1^2=\frac{1}{2}\left({\omega }_x^2+{\omega }_{\theta }^2+\sqrt{{({\omega }_x^2+{\omega }_{\theta }^2)}^2-4\left({\omega }_x^2·{\omega }_{\theta }^2-\frac{{\epsilon }^2}{4mI}\right)}\right)= \\ \frac{1}{2}\left({\omega }_x^2+{\omega }_{\theta }^2+\sqrt{{({\omega }_x^2-{\omega }_{\theta }^2)}^2+\frac{{\epsilon }^2}{mI}}\right)\\ {\omega }_2^2=\frac{1}{2}\left({\omega }_x^2+{\omega }_{\theta }^2-\sqrt{{({\omega }_x^2-{\omega }_{\theta }^2)}^2+\frac{{\epsilon }^2}{mI}}\right)\end{array}} \end{gathered}$$

La forma general del ángulo θ de rotación en función del tiempo t es una combinación de los dos modos normales de vibración

θ(t)=Asin(ω₁t)+ Bcos(ω₁t)+ Csin(ω₂t)+ Dcos(ω₂t)

La velocidad angular de rotación es

${\displaystyle \frac{d\theta }{dt}={\omega }_1\left(A\text{cos}({\omega }_{1}t)-B\sin ({\omega }_{1}t)\right)+{\omega }_2\left(C\cos ({\omega }_{2}t)-D\sin ({\omega }_{2}t)\right)}$

Para calcular la posición x(t), se introduce θ(t) y su derivada segunda en la ecuación diferencial de segundo orden que describe la rotación del cilindro.

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}+\frac{k_{\theta }}{I}\theta +\frac{\epsilon x}{2I}=0\\ x(t)=\frac{2I}{\epsilon }\{\begin{array}{l}\left({\omega }_1^2-{\omega }_{\theta }^2\right)\left(A\sin ({\omega }_{1}t)+B\cos ({\omega }_{1}t)\right)+\\ \left({\omega }_2^2-{\omega }_{\theta }^2\right)\left(C\sin ({\omega }_{2}t)+D\cos ({\omega }_{2}t)\right)\end{array}\end{array}}$

La velocidad del c.m. del cilindro es

${\displaystyle \frac{dx}{dt}=\frac{2I}{\epsilon }\{\begin{array}{l}\left({\omega }_1^2-{\omega }_{\theta }^2\right){\omega }_1\left(A\cos ({\omega }_{1}t)-B\sin ({\omega }_{1}t)\right)+\\ \left({\omega }_2^2-{\omega }_{\theta }^2\right){\omega }_2\left(C\cos ({\omega }_{2}t)-D\sin ({\omega }_{2}t)\right)\end{array}}$

Las condiciones iniciales determinan los valores de los coeficientes A, B, C, D.

Desplazamos el cilindro x₀ y lo giramos un ángulo θ₀ y a continuación lo soltamos. La velocidad inicial es dx/dt=0, dθ/dt=0 en el instante t=0.

Resolvemos el sistema de cuatro ecuaciones

${\displaystyle \begin{array}{l}{x}_0=\frac{2I}{\epsilon }\left\{\left({\omega }_1^2-{\omega }_{\theta }^2\right)B+\left({\omega }_2^2-{\omega }_{\theta }^2\right)D\right\}\\ 0=\frac{2I}{\epsilon }\left\{\left({\omega }_1^2-{\omega }_{\theta }^2\right){\omega }_{1}A+\left({\omega }_2^2-{\omega }_{\theta }^2\right){\omega }_{2}C\right\}\\ {\theta }_0=B+D\\ 0={\omega }_{1}A+{\omega }_{2}C\end{array}}$

Despejamos las incógnitas A, B, C, y D

A=C=0

${\displaystyle B=-\frac{\frac{\epsilon x_0}{2I}-({\omega }_2^2-{\omega }_{\theta }^2){\theta }_0}{({\omega }_2^2-{\omega }_1^2)}D=\frac{\frac{\epsilon x_0}{2I}-({\omega }_1^2-{\omega }_{\theta }^2){\theta }_0}{({\omega }_2^2-{\omega }_1^2)}}$

Las expresiones de la posición x y θ y velocidad dx/dt y dθ/dt en función del tiempo son

θ(t)= Bcos(ω₁t)+ Dsin(ω₂t)

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=-{\omega }_{1}B\sin ({\omega }_{1}t)-{\omega }_{2}D\sin ({\omega }_{2}t)\\ x(t)=\frac{2I}{\epsilon }\left\{\left({\omega }_1^2-{\omega }_{\theta }^2\right)B\cos ({\omega }_{1}t)+\left({\omega }_2^2-{\omega }_{\theta }^2\right)D\cos ({\omega }_{2}t)\right\}\\ \frac{dx}{dt}=-\frac{2I}{\epsilon }\left\{\left({\omega }_1^2-{\omega }_{\theta }^2\right){\omega }_{1}B\sin ({\omega }_{1}t)+\left({\omega }_2^2-{\omega }_{\theta }^2\right){\omega }_{2}D\sin ({\omega }_{2}t)\right\}\end{array}}$

Modos normales de vibración

• El modo 1 de frecuencia angular ω₁, se obtiene cuando D=0,

La relación entre la posición inicial x₀ del cilindro y el ángulo inicial de giro θ₀ es

${\displaystyle x_0=\frac{2I}{\epsilon }({\omega }_1^2-{\omega }_{\theta }^2){\theta }_0}$

La posición x del cilindro y el ángulo girado θ en función del tiempo t son

${\displaystyle \begin{array}{l}\theta (t)={\theta }_0\cos ({\omega }_{1}t)\\ x(t)=\frac{2I}{\epsilon }\left({\omega }_1^2-{\omega }_{\theta }^2\right){\theta }_0\cos ({\omega }_{1}t)\end{array}}$

• El modo 2 de frecuencia angular ω₂, se obtiene cuando B=0,

${\displaystyle x_0=\frac{2I}{\epsilon }({\omega }_2^2-{\omega }_{\theta }^2){\theta }_0}$

La posición x del cilindro y el ángulo girado θ en función del tiempo t son

${\displaystyle \begin{array}{l}\theta (t)={\theta }_0\cos ({\omega }_{2}t)\\ x(t)=\frac{2}{\epsilon }\left({\omega }_1^2-{\omega }_{\theta }^2\right){\theta }_0\cos ({\omega }_{2}t)\end{array}}$

Cuando las frecuencias son iguales

Si modificamos el momento de inercia I, cambiando la distancia d de las esferas al eje de rotación podemos conseguir que la frecuencia angular de las oscilaciones longitudinales ω_x y la frecuencia angular de las oscilaciones torsionales ω_θ sean iguales ω =ω_x=ω_θ

Las frecuencias ω₁ y ω₂ de los modos normales de vibración tienen una expresión mucho más simple

${\displaystyle {\omega }_1^2={\omega }^2+\sqrt{\frac{{\epsilon }^2}{4mI}}{\omega }_2^2={\omega }^2-\sqrt{\frac{{\epsilon }^2}{4mI}}}$

Es importante analizar el caso de que x₀=0. Se gira el cilindro un ángulo inicial θ₀ y luego, se suelta.

Los coeficientes B=D=θ₀/2. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\theta (t)=\frac{{\theta }_0}{2}\left(\cos ({\omega }_{1}t)+\cos ({\omega }_{2}t)\right)\\ x(t)=\frac{{\theta }_0}{2}\sqrt{\frac{I}{m}}\left(\cos ({\omega }_{1}t)-\cos ({\omega }_{2}t)\right)\end{array}}$

• La relación entre la posición inicial x₀ del cilindro y el ángulo inicial de giro θ₀ es en el modo normal 1 de frecuencia angular ω₁ es

${\displaystyle x_0=+\sqrt{\frac{I}{m}}{\theta }_0}$

• La relación entre la posición inicial x₀ del cilindro y el ángulo inicial de giro θ₀ es en el modo normal 2 de frecuencia angular ω₂ es

${\displaystyle x_0=-\sqrt{\frac{I}{m}}{\theta }_0}$

Ejemplo:

• Constante de acoplamiento, ε=0.03 kg·m/s²
• Masa del cilindro y las esferas, m=0.43 kg
• Constante elástica, k_x =16.98 N/m

Frecuencia angular del movimiento de traslación es

${\displaystyle {\omega }_x=\sqrt{\frac{16.98}{0.43}}=6.284\text{rad/s}}$

• Constante elástica, k_θ=5.74·10^-3 Nm

• Momento de inercia I es variable

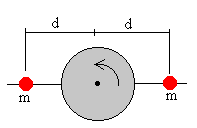
El momento de inercia I respecto del eje de rotación se puede variar, moviendo dos pequeñas esferas de igual masa m situadas a la misma distancia d del eje de rotación.

El momento de inercia del sistema, será igual al momento de inercia del cuerpo cilíndrico 1.28·10^-4 kg·m² más el momento de inercia de las dos esferas consideradas como masas puntuales de 3.4·10^-3 kg cada una.

I=1.28·10^-4+2·3.4·10^-3·d² kg m²

La frecuencia angular ω_θ de las oscilaciones torsionales se puede cambiar modificando el momento de inercia I es decir, la distancia d de las pequeñas esferas, al eje de rotación.

${\displaystyle {\omega }_{\theta }=\sqrt{\frac{5.74·{10}^{-3}}{I}}}$

Para d=3.5 cm=0.035 m, el momento de inercia I=1.3633·10^-4 kg m², la frecuencia angular de las oscilaciones torsionales es ω_θ=6.489 rad/s

masa=0.43;  %masa del bloque
inerciaIni=1.28e-4; %inercia de la varilla soporte
cteTorsion=5.74e-3;
cteElastica=16.98;
acoplamiento=0.03;
masaEsfera=3.4e-3;  %masa de las dos partículas 

dist=0.035; %distancia de las esferas al eje
x0=-0.04; %Posición inicial del bloque
y0=0; %ángulo inicial 

inercia=inerciaIni+2*masaEsfera*dist*dist;
wx2=cteElastica/masa;
wy2=cteTorsion/inercia;
w1=(wx2+wy2+sqrt((wx2-wy2)*(wx2-wy2)
+acoplamiento*acoplamiento/(masa*inercia)))/2;
w2=(wx2+wy2-sqrt((wx2-wy2)*(wx2-wy2)
+acoplamiento*acoplamiento/(masa*inercia)))/2;
B=-(acoplamiento*x0/(2*inercia)-(w2-wy2)*y0)/(w2-w1);
D=(acoplamiento*x0/(2*inercia)-(w1-wy2)*y0)/(w2-w1);

t=linspace(0,30,400); 
x=(2.0/acoplamiento)*((inercia*w1-cteTorsion)*B*cos(sqrt(w1)*t)
+ (inercia*w2-cteTorsion)*D*cos(sqrt(w2)*t));
y=B*cos(sqrt(w1)*t)+D*cos(sqrt(w2)*t);
figure
plot(t,x)
grid on
xlabel('t')
ylabel('x')
title('Posición en función del tiempo')
figure
plot(t,y)
set(gca,'YTick',-pi/2:pi/6:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-\pi/3','-\pi/6','0','\pi/6',
'\pi/3','\pi/2' })
grid on
xlabel('t')
ylabel('\theta')
title('Posición angular en función del tiempo')

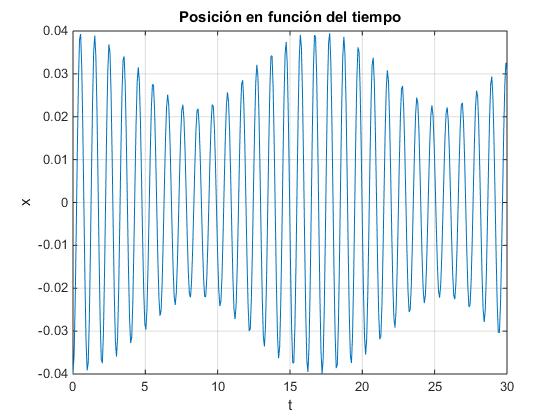
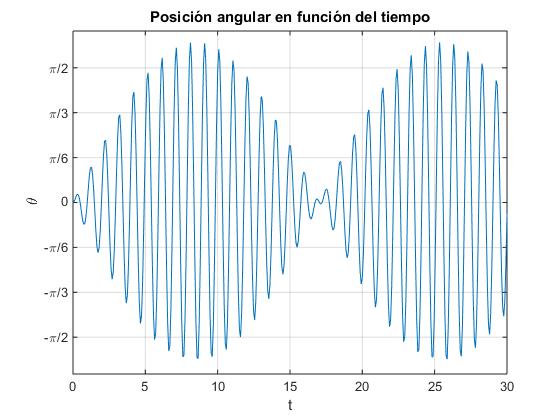
Las frecuencias de los modos normales de oscilación 1 y 2 valen

ω₁=6.569 rad/s
ω₂=6.200 rad/s

Si la posición inicial del cilindro x₀=-0.04, el ángulo que hemos de girar para observar el primer modo normal de oscilación es

θ₀=-4.20 rad=-240.7º

para observar el segundo modo normal de oscilación es

θ₀=1.20 rad=68.8º

Modificamos la distancia d o el momento de inercia I hasta lograr que ambas frecuencias sean iguales. Los valores de dichas frecuencias aparecen en la parte inferior la frecuencia ω_x, y en la parte superior ω_θ.

El valor de d que hace que ambas frecuencias sean iguales es

${\displaystyle \frac{16.98}{0.43}=\frac{5.74·{10}^{-3}}{1.28·{10}^{-4}+2·3.4·{10}^{-3}{d}^2}d=0.051\text{m}}$

El momento de inercia vale I=1.45·10^-4 kg m²

La frecuencias angulares ω_x=ω_θ=6.284 rad/s

Las frecuencias de los modos normales de oscilación 1 y 2 valen

ω₁=6.433 rad/s
ω₂=6.131 rad/s

Si la posición inicial del cilindro x₀=-0.04, el ángulo que hemos de girar para observar el primer modo normal de oscilación es

θ₀=-2.18 rad=-124.6º

para observar el segundo modo normal de oscilación es

θ₀=2.18 rad=124.6º

Es importante examinar el caso de que x₀=0 y θ₀≠0, por ejemplo, θ₀=0.70 rad=40º

θ(t)=20(cos(ω₁t)+ cos(ω₂t)) grados
x(t)=0.64(cos(ω₁t)-cos(ω₂t)) cm

Balance energético

Se puede observar los cambios energéticos en el diagrama en forma de tarta a la derecha. En distintos colores se representan las energías potenciales elásticas y las energías cinéticas correspondientes a ambos modos de oscilación.

Energías correspondientes a las oscilaciones longitudinales

• Energía potencial $\frac{1}{2}{k}_x{x}^2$
• Energía cinética $\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2$

Energías correspondientes a las oscilaciones torsionales

• Energía potencial $\frac{1}{2}{k}_{\theta }{\theta }^2$
• Energía cinética $\frac{1}{2}I{\left(\frac{d\theta }{dt}\right)}^2$

Energía de acoplamiento$\frac{1}{2}\epsilon x\theta$

En la parte superior derecha, se proporciona el valor numérico de la energía total que se mantiene constante durante el movimiento del péndulo.

Un diagrama de barras nos muestra como se distribuye la energía total. Se ha de tener en cuenta, que la energía de acoplamiento puede ser positiva o negativa, las restantes energías son positivas.

Actividades

Se introduce

• La posición inicial vertical x₀ del cilindro en cm, en el control titulado Altura
• El ángulo de giro inicial θ₀ en grados, en el control titulado Angulo
• La posición de las masas en el control Posición masas, hacia el centro para disminuir el momento de inercia, hacia fuera para aumentarlo.

Se pulsa el botón titulado Nuevo

Referencias

Berg R. H, Marshall T. Wilberforce pendulum oscillations and normal modes. Am. J. Phys. 59 (1) January 1991, pp. 32-38.