Sistema formado por n péndulos acoplados (I)

Un péndulo

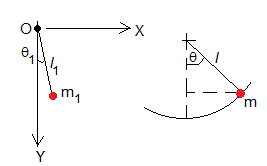
Las coordenadas de la primera partícula son x₁=l₁sinθ₁, y₁=l₁cosθ₁. Derivando con respecto del tiempo obtenemos la velocidad.

$\vec{v_{1}} = \frac{d x_{1}}{d t} \hat{i} + \frac{d y_{1}}{d t} \hat{j} = l_{1} (\cos θ_{1} \hat{i} - \sin θ_{1} \hat{j}) \frac{d θ_{1}}{d t}$

La energía cinética, T₁ y potencial, V₁ son, respectivamente

$\begin{array}{l} T_{1} = \frac{1}{2} m_{1} l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} \\ V_{1} = m_{1} g l_{1} (1 - \cos θ_{1}) \end{array}$

Para ángulos θ pequeños, hacemos la aproximación 1-cosθ≈θ²/2

La lagrangiana L₁=T₁-V₁ es

$L_{1} = \frac{1}{2} m_{1} l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} - \frac{1}{2} m_{1} g l_{1} θ_{1}^{2}$

La ecuación del movimiento

$\begin{array}{l} \frac{d}{d t} (\frac{\partial L_{1}}{\partial {\dot{θ}}_{1}}) - \frac{\partial L_{1}}{\partial θ_{1}} = 0 \\ m_{1} l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + m_{1} g θ_{1} = 0 \end{array}$

La solución de esta ecuación diferencial es θ₁=Asin(ωt)+Bcos(ωt), con ω²=g/l₁. Los coeficientes A y B se determinan a partir de las condiciones iniciales (posición y velocidad)

Dos péndulos acoplados

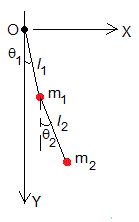
Las coordenadas de la segunda partícula son x₂=x₁+l₂sinθ₂, y₂=y₁+l₂cosθ₂. Derivando con respecto del tiempo obtenemos la velocidad.

$\begin{array}{l} \vec{v_{2}} = \frac{d x_{2}}{d t} \hat{i} + \frac{d y_{2}}{d t} \hat{j} = \\ (l_{1} \cos θ_{1} \frac{d θ_{1}}{d t} + l_{2} \cos θ_{2} \frac{d θ_{2}}{d t}) \hat{i} - (l_{1} \sin θ_{1} \frac{d θ_{1}}{d t} + l_{2} \sin θ_{2} \frac{d θ_{2}}{d t}) \hat{j} \end{array}$

La energía cinética, T₂ y potencial, V₂ son, respectivamente

$\begin{array}{l} T_{2} = \frac{1}{2} m_{2} {l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + 2 l_{1} l_{2} \cos (θ_{1} - θ_{2}) \frac{d θ_{1}}{d t} \frac{d θ_{2}}{d t}} \\ V_{2} = m_{2} g {l_{1} (1 - \cos θ_{1}) + l_{2} (1 - \cos θ_{2})} \end{array}$

Para ángulos θ₁ y θ₂ pequeños, hacemos la aproximación cos(θ₁-θ₂)≈1

La lagrangiana L₂=L₁+T₂-V₂ es

$L_{2} = \frac{1}{2} (m_{1} + m_{2}) l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + m_{2} l_{1} l_{2} \frac{d θ_{1}}{d t} \frac{d θ_{2}}{d t} - \frac{1}{2} (m_{1} + m_{2}) g l_{1} θ_{1}^{2} - \frac{1}{2} m_{2} g l_{2} θ_{2}^{2}$

Las ecuaciones del movimiento

${\begin{cases} (m_{1} + m_{2}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + m_{2} l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + (m_{1} + m_{2}) g θ_{1} = 0 \\ m_{2} l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + m_{2} l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + m_{2} g θ_{2} = 0 \end{cases}$

Que son las ecuaciones del movimiento del péndulo doble cuando nos restringimos a pequeños valores de los ángulos θ₁ y θ₂

Cuando m₁=m₂=m, y l₁=l₂=l. Las ecuaciones del movimiento son

${\begin{cases} 2 \frac{d^{2} θ_{1}}{d t^{2}} + \frac{d^{2} θ_{2}}{d t^{2}} + 2 \frac{g}{l} θ_{1} = 0 \\ \frac{d^{2} θ_{1}}{d t^{2}} + \frac{d^{2} θ_{2}}{d t^{2}} + \frac{g}{l} θ_{2} = 0 \end{cases}$

La forma general del ángulo θ₁ en función del tiempo t es una combinación de los dos modos normales de vibración de frecuencias ω₁ y ω₂ que calcularemos más adelante.

θ₁(t)=A₁sin(ω₁t)+ B₁cos(ω₁t)+ C₁sin(ω₂t)+ D₁cos(ω₂t)

Lo mismo para θ₂

θ₂(t)=A₂sin(ω₁t)+ B₂cos(ω₁t)+ C₂sin(ω₂t)+ D₂cos(ω₂t)

Las dos ecuaciones diferenciales proporcionan cuatro relaciones entre los coeficientes y las condiciones iniciales (posición y velocidad) otras cuatro de las que se despejan, A₁, A₂, B₁, B₂, C₁, C₂. Como hemos visto en el péndulo doble, siempre es posible encontrar las condiciones iniciales que hacen que algunos coeficientes sean cero. De modo que, la solución más simple sea θ₁=A₁sin(ω₁t), θ₂=A₂sin(ω₁t), para ω₁, y θ₁=C₁sin(ω₂t), θ₂=C₂sin(ω₂t), para ω₂.

Vamos a calcular y representar los modos normales de vibración. Suponiendo una solución de la forma θ ₁=A₁sin(ωt), θ₂=A₂sin(ωt), obtenemos el sistema de ecuaciones

${\begin{cases} 2 (\frac{g}{l} - ω^{2}) A_{1} - ω^{2} A_{2} = 0 \\ - ω^{2} A_{1} + (\frac{g}{l} - ω^{2}) A_{2} = 0 \end{cases}$

En este sistema homogéneo de dos ecuaciones con dos incógnitas, el determinante de los coeficientes ha de ser cero

$\begin{array}{l} | \begin{matrix} 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} | = 0 \\ ω^{4} - 4 \frac{g}{l} ω^{2} + 2 \frac{g^{2}}{l^{2}} = 0 {\begin{cases} ω_{1}^{2} = \frac{g}{l} (2 - \sqrt{2}) \\ ω_{2}^{2} = \frac{g}{l} (2 + \sqrt{2}) \end{cases} \end{array}$

Frecuencias que ya hemos obtenido al estudiar el péndulo doble (amplitudes pequeñas)

Tomamos la segunda ecuación del sistema homogéneo de dos ecuaciones, para calcular la amplitud A₂ en términos de la amplitud A₁

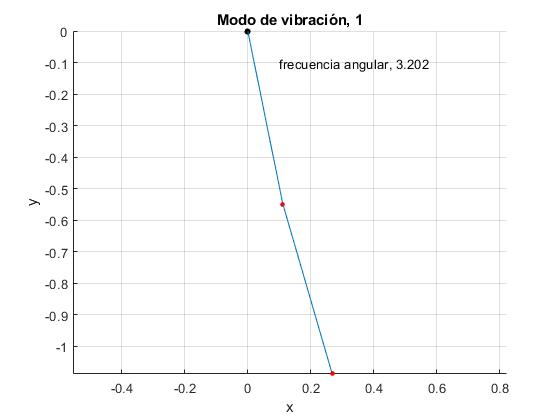
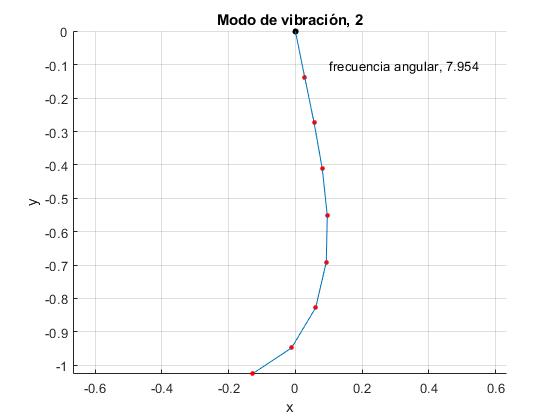
$\begin{array}{l} - ω^{2} A_{1} + (\frac{g}{l} - ω^{2}) A_{2} = 0 \\ A_{2} = \frac{ω^{2}}{\frac{g}{l} - ω^{2}} A_{1} \end{array}$

Calculamos A₂ para el primer modo de vibración de frecuencia angular ω=ω₁. El ángulo θ₁ que forma el primer péndulo con la vertical será proporcional a A₁ y el ángulo θ₂ que forma el segundo péndulo con la vertical será proporcional a A₂. Representamos el primer modo de vibración.

L=1.12; %longitud total
n=2; %número de péndulos
w2=[2-sqrt(2), 2+sqrt(2)]*9.8/(L/n); %cuadrado frecuencias
A1=0.2; %escala
iModo=1; %modo de vibración
A2=w2(iModo)*A1/(9.8/(L/n)-w2(iModo));
angulos=[A1,A2];

hold on
x1=0; y1=0; %origen
plot(x1,y1,'ko','markersize',4,'markerfacecolor','k')
for j=1:n
    x2=x1+(L/n)*sin(angulos(j));
    y2=y1-(L/n)*cos(angulos(j));
    line([x1,x2],[y1,y2])
    plot(x2,y2,'ro','markersize',3,'markerfacecolor','r')
    x1=x2;
    y1=y2;
end
text(0.1,-0.1, sprintf('frecuencia angular, %1.3f',sqrt(w2(iModo))))
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title(sprintf('Modo de vibración, %i',iModo))

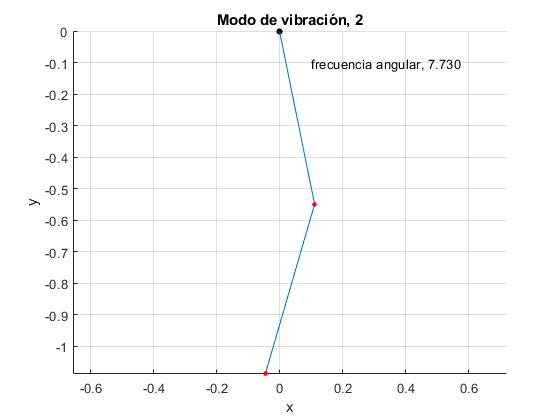
Repetimos para el segundo modo de vibración de frecuencia angular ω=ω₂, cambiando el valor de la variable iModo=2

Tres péndulos

Las coordenadas de la tercera partícula son x₃=x₂+l₃sinθ₃, y₃=y₂+l₃cosθ₃. Derivando con respecto del tiempo obtenemos la velocidad.

$\vec{v_{3}} = \frac{d x_{3}}{d t} \hat{i} + \frac{d y_{3}}{d t} \hat{j} = (l_{1} \cos θ_{1} \frac{d θ_{1}}{d t} + l_{2} \cos θ_{2} \frac{d θ_{2}}{d t} + l_{3} \cos θ_{3} \frac{d θ_{3}}{d t}) \hat{i} - (l_{1} \sin θ_{1} \frac{d θ_{1}}{d t} + l_{2} \sin θ_{2} \frac{d θ_{2}}{d t} + l_{3} \sin θ_{3} \frac{d θ_{3}}{d t}) \hat{j}$

La energía cinética, T₃ y potencial, V₃ son, respectivamente

$\begin{array}{l} T_{3} = \frac{1}{2} m_{2} {l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + l_{3}^{2} {(\frac{d θ_{3}}{d t})}^{2} + 2 l_{1} l_{2} \cos (θ_{1} - θ_{2}) \frac{d θ_{1}}{d t} \frac{d θ_{2}}{d t} + 2 l_{1} l_{3} \cos (θ_{1} - θ_{3}) \frac{d θ_{1}}{d t} \frac{d θ_{3}}{d t} + 2 l_{2} l_{3} \cos (θ_{2} - θ_{3}) \frac{d θ_{2}}{d t} \frac{d θ_{3}}{d t}} \\ V_{3} = m_{3} g {l_{1} (1 - \cos θ_{1}) + l_{2} (1 - \cos θ_{2}) + l_{3} (1 - \cos θ_{3})} \end{array}$

Para ángulos θ₁, θ₂ y θ₃ pequeños, hacemos la aproximación cos(θ₁-θ₂)≈1, cos(θ₁-θ₃)≈1 y cos(θ₂-θ₃)≈1

La lagrangiana L₃=L₂+T₃-V₃ es

$\begin{array}{l} L_{3} = \frac{1}{2} (m_{1} + m_{2} + m_{3}) l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} (m_{2} + m_{3}) l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + \frac{1}{2} m_{3} l_{3}^{2} {(\frac{d θ_{3}}{d t})}^{2} + (m_{2} + m_{3}) l_{1} l_{2} \frac{d θ_{1}}{d t} \frac{d θ_{2}}{d t} \\ + m_{3} l_{1} l_{3} \frac{d θ_{1}}{d t} \frac{d θ_{3}}{d t} + m_{3} l_{2} l_{3} \frac{d θ_{2}}{d t} \frac{d θ_{3}}{d t} - \frac{1}{2} (m_{1} + m_{2} + m_{3}) g l_{1} θ_{1}^{2} - \frac{1}{2} (m_{2} + m_{3}) g l_{2} θ_{2}^{2} - \frac{1}{2} m_{3} g l_{3} θ_{3}^{2} \end{array}$

Las ecuaciones del movimiento

${\begin{cases} (m_{1} + m_{2} + m_{3}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + (m_{2} + m_{3}) l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + m_{3} l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + (m_{1} + m_{2} + m_{3}) g θ_{1} = 0 \\ (m_{2} + m_{3}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + (m_{2} + m_{3}) l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + m_{3} l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + (m_{2} + m_{3}) g θ_{2} = 0 \\ m_{3} l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + m_{3} l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + m_{3} l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + m_{3} g θ_{3} = 0 \end{cases}$

Cuando m₁=m₂=m₃=m, y l₁=l₂=l₃=l. Las ecuaciones del movimiento son

${\begin{cases} 3 \frac{d^{2} θ_{1}}{d t^{2}} + 2 \frac{d^{2} θ_{2}}{d t^{2}} + \frac{d^{2} θ_{3}}{d t^{2}} + 3 \frac{g}{l} θ_{1} = 0 \\ 2 \frac{d^{2} θ_{1}}{d t^{2}} + 2 \frac{d^{2} θ_{2}}{d t^{2}} + \frac{d^{2} θ_{3}}{d t^{2}} + 2 \frac{g}{l} θ_{2} = 0 \\ \frac{d^{2} θ_{1}}{d t^{2}} + \frac{d^{2} θ_{2}}{d t^{2}} + \frac{d^{2} θ_{3}}{d t^{2}} + \frac{g}{l} θ_{3} = 0 \end{cases}$

Vamos a calcular y representar los modos normales de vibración. Suponiendo una solución θ₁=A₁sin(ωt), θ₂=A₂sin(ωt), θ₃=A₃sin(ωt), obtenemos el sistema de ecuaciones

${\begin{cases} 3 (\frac{g}{l} - ω^{2}) A_{1} - 2 ω^{2} A_{2} - ω^{2} A_{3} = 0 \\ - 2 ω^{2} A_{1} + 2 (\frac{g}{l} - ω^{2}) A_{2} - ω^{2} A_{3} = 0 \\ - ω^{2} A_{1} - ω^{2} A_{2} + (\frac{g}{l} - ω^{2}) A_{3} = 0 \end{cases}$

En este sistema homogéneo de tres ecuaciones con tres incógnitas, el determinante de los coeficientes ha de ser cero

$| \begin{matrix} 3 (\frac{g}{l} - ω^{2}) & - 2 ω^{2} & - ω^{2} \\ - 2 ω^{2} & 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} | = 0$

Obtenemos la ecuación cúbica en ω². En el código x es ω² y g es g/l

>> syms g x;
>> A = [3*(g - x),-2*x,-x; -2*x,2*(g - x),-x;-x,-x, g - x];
>> det(A)
ans = 6*g^3 - 18*g^2*x + 9*g*x^2 - x^3

$ω^{6} - 9 \frac{g}{l} ω^{4} + 18 \frac{g^{2}}{l^{2}} ω^{2} - 6 \frac{g^{3}}{l^{3}} = 0$

Los cuadrados de las frecuencias de los modos normales de vibración son las raíces de esta ecuación

>> n=3; %número de péndulos
>> L=1.12; %longitud total
>> roots([1, -9*9.8/(L/n),18*9.8^2/(L/n)^2,-6*9.8^3/(L/n)^3])
ans =
  165.1111
   60.2249
   10.9141

Tomamos la segunda y tercera ecuación del sistema homogéneo de tres ecuaciones, para calcular las amplitudes A₂ y A₃ en términos de la amplitud A₁

$\begin{array}{l} {\begin{cases} 2 (\frac{g}{l} - ω^{2}) A_{2} - ω^{2} A_{3} = 2 ω^{2} A_{1} \\ - ω^{2} A_{2} + (\frac{g}{l} - ω^{2}) A_{3} = ω^{2} A_{1} \end{cases} \\ A_{2} = \frac{| \begin{matrix} 2 & - ω^{2} \\ 1 & (\frac{g}{l} - ω^{2}) \end{matrix} |}{| \begin{matrix} 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} |} ω^{2} A_{1} = \frac{2 \frac{g}{l} - ω^{2}}{ω^{4} + 2 \frac{g^{2}}{l^{2}} - 4 \frac{g}{l} ω^{2}} ω^{2} A_{1} \\ A_{3} = \frac{| \begin{matrix} 2 (\frac{g}{l} - ω^{2}) & 2 \\ - ω^{2} & 1 \end{matrix} |}{| \begin{matrix} 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} |} ω^{2} A_{1} = \frac{2 \frac{g}{l}}{ω^{4} + 2 \frac{g^{2}}{l^{2}} - 4 \frac{g}{l} ω^{2}} ω^{2} A_{1} \end{array}$

Calculamos A₂ y A₃ para el primer modo de vibración de frecuencia angular ω=ω₁. El ángulo θ₁ que forma el primer péndulo con la vertical será proporcional a A₁, el ángulo θ₂ que forma el segundo péndulo con la vertical será proporcional a A₂ y el ángulo θ₃ que forma el tercer péndulo con la vertical será proporcional a A₃. Representamos el primer modo de vibración.

L=1.12; %longitud total
n=3; %número de péndulos
%cuadrado frecuencias ordenadas
w2=sort(roots([1, -9*9.8/(L/n),18*9.8^2/(L/n)^2,-6*9.8^3/(L/n)^3])); 
iModo=1; %modo de vibración
A1=0.2; %escala
den=(w2(iModo)^2+2*9.8^2/(L/n)^2-4*w2(iModo)*9.8/(L/n)); %denominador
A2=(2*9.8/(L/n)-w2(iModo))*A1*w2(iModo)/den;
A3=2*9.8/(L/n)*A1*w2(iModo)/den;
angulos=[A1,A2,A3];

hold on
x1=0; y1=0;
plot(x1,y1,'ko','markersize',4,'markerfacecolor','k')
for j=1:n
    x2=x1+(L/n)*sin(angulos(j));
    y2=y1-(L/n)*cos(angulos(j));
    line([x1,x2],[y1,y2])
    plot(x2,y2,'ro','markersize',3,'markerfacecolor','r')
    x1=x2;
    y1=y2;
end
text(0.1,-0.1, sprintf('frecuencia angular, %1.3f',sqrt(w2(iModo))))
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title(sprintf('Modo de vibración, %i',iModo))

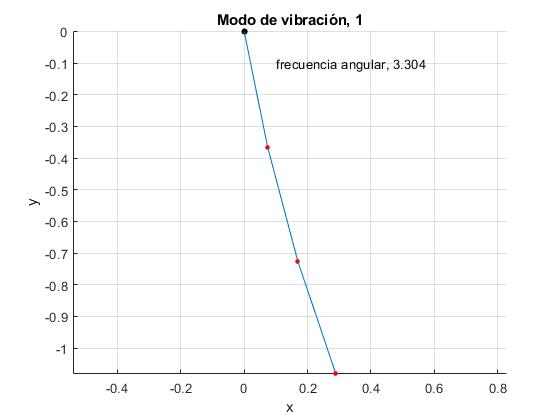
Repetimos para el segundo modo de vibración de frecuencia angular ω=ω₂, cambiando el valor de la variable iModo=2

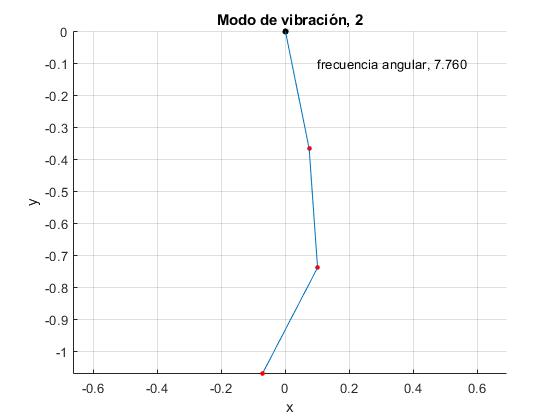
Repetimos para el tercer modo de vibración de frecuencia angular ω=ω₃, cambiando el valor de la variable iModo=3

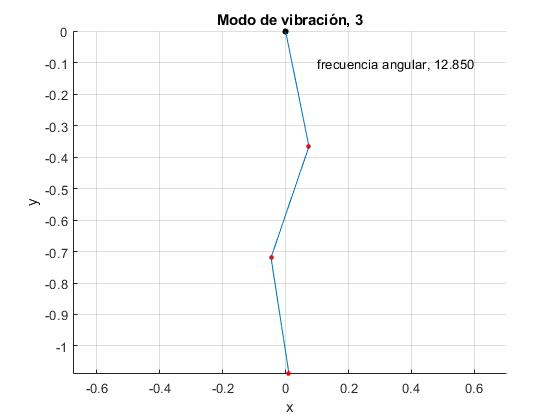
Cuatro péndulos

Las coordenadas de la cuarta partícula son x₄=x₃+l₄sinθ₄, y₄=y₃+l₄cosθ₄. Derivando con respecto del tiempo obtenemos la velocidad.

$\vec{v_{4}} = \frac{d x_{4}}{d t} \hat{i} + \frac{d y_{4}}{d t} \hat{j} = (l_{1} \cos θ_{1} \frac{d θ_{1}}{d t} + l_{2} \cos θ_{2} \frac{d θ_{2}}{d t} + l_{3} \cos θ_{3} \frac{d θ_{3}}{d t} + l_{4} \cos θ_{4} \frac{d θ_{4}}{d t}) \hat{i} - (l_{1} \sin θ_{1} \frac{d θ_{1}}{d t} + l_{2} \sin θ_{2} \frac{d θ_{2}}{d t} + l_{3} \sin θ_{3} \frac{d θ_{3}}{d t} + l_{4} \sin θ_{4} \frac{d θ_{4}}{d t}) \hat{j}$

La energía cinética, T₄ y potencial, V₄ son, respectivamente

$\begin{array}{l} T_{4} = \frac{1}{2} m_{4} {\begin{cases} l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + l_{3}^{2} {(\frac{d θ_{3}}{d t})}^{2} + l_{4}^{2} {(\frac{d θ_{4}}{d t})}^{2} + 2 l_{1} l_{2} \cos (θ_{1} - θ_{2}) \frac{d θ_{1}}{d t} \frac{d θ_{2}}{d t} + 2 l_{1} l_{3} \cos (θ_{1} - θ_{3}) \frac{d θ_{1}}{d t} \frac{d θ_{3}}{d t} + \\ 2 l_{1} l_{4} \cos (θ_{1} - θ_{4}) \frac{d θ_{1}}{d t} \frac{d θ_{4}}{d t} + 2 l_{2} l_{3} \cos (θ_{2} - θ_{3}) \frac{d θ_{2}}{d t} \frac{d θ_{3}}{d t} + 2 l_{2} l_{4} \cos (θ_{2} - θ_{4}) \frac{d θ_{2}}{d t} \frac{d θ_{4}}{d t} + 2 l_{3} l_{4} \cos (θ_{3} - θ_{4}) \frac{d θ_{3}}{d t} \frac{d θ_{4}}{d t} \end{cases}} \\ V_{4} = m_{4} g {l_{1} (1 - \cos θ_{1}) + l_{2} (1 - \cos θ_{2}) + l_{3} (1 - \cos θ_{3}) + l_{4} (1 - \cos θ_{4})} \end{array}$

Para ángulos θ₁, θ₂, θ₃ y θ₄ pequeños, hacemos la aproximación cos(θ₁-θ₂)≈1, cos(θ₁-θ₃)≈1, cos(θ₁-θ₄)≈1, cos(θ₂-θ₃)≈1, cos(θ₂-θ₄)≈1 y cos(θ₃-θ₄)≈1

La lagrangiana L₄=L₃+T₄-V₄ es

$\begin{array}{l} L_{4} = \frac{1}{2} (m_{1} + m_{2} + m_{3} + m_{4}) l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} (m_{2} + m_{3} + m_{4}) l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + \frac{1}{2} (m_{3} + m_{4}) l_{3}^{2} {(\frac{d θ_{3}}{d t})}^{2} + \frac{1}{2} m_{4} l_{4}^{2} {(\frac{d θ_{4}}{d t})}^{2} + \\ (m_{2} + m_{3} + m_{4}) l_{1} l_{2} \frac{d θ_{1}}{d t} \frac{d θ_{2}}{d t} + (m_{3} + m_{4}) l_{1} l_{3} \frac{d θ_{1}}{d t} \frac{d θ_{3}}{d t} + m_{4} l_{1} l_{4} \frac{d θ_{1}}{d t} \frac{d θ_{4}}{d t} + (m_{3} + m_{4}) l_{2} l_{3} \frac{d θ_{2}}{d t} \frac{d θ_{3}}{d t} + m_{4} l_{2} l_{4} \frac{d θ_{2}}{d t} \frac{d θ_{4}}{d t} \\ + m_{4} l_{3} l_{4} \frac{d θ_{3}}{d t} \frac{d θ_{4}}{d t} - \frac{1}{2} (m_{1} + m_{2} + m_{3} + m_{4}) g l_{1} θ_{1}^{2} - \frac{1}{2} (m_{2} + m_{3} + m_{4}) g l_{2} θ_{2}^{2} - \frac{1}{2} (m_{3} + m_{4}) g l_{3} θ_{3}^{2} - \frac{1}{2} m_{4} g l_{4} θ_{4}^{2} \end{array}$

Las ecuaciones del movimiento

${\begin{cases} (m_{1} + m_{2} + m_{3} + m_{4}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + (m_{2} + m_{3} + m_{4}) l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + (m_{3} + m_{4}) l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + m_{4} l_{4} \frac{d^{2} θ_{4}}{d t^{2}} + (m_{1} + m_{2} + m_{3} + m_{4}) g θ_{1} = 0 \\ (m_{2} + m_{3} + m_{4}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + (m_{2} + m_{3} + m_{4}) l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + (m_{3} + m_{4}) l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + m_{4} l_{4} \frac{d^{2} θ_{4}}{d t^{2}} + (m_{2} + m_{3} + m_{4}) g θ_{2} = 0 \\ (m_{3} + m_{4}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + (m_{3} + m_{4}) l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + (m_{3} + m_{4}) l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + m_{4} l_{4} \frac{d^{2} θ_{4}}{d t^{2}} + (m_{3} + m_{4}) g θ_{3} = 0 \\ m_{4} l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + m_{4} l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + m_{4} l_{3} \frac{d^{2} θ_{3}}{d t^{2}} + m_{4} l_{4} \frac{d^{2} θ_{4}}{d t^{2}} + m_{4} g θ_{4} = 0 \end{cases}$

Cuando m₁=m₂=m₃=m₄=m, y l₁=l₂=l₃=l₄=l. Las ecuaciones del movimiento son

${\begin{cases} 4 \frac{d^{2} θ_{1}}{d t^{2}} + 3 \frac{d^{2} θ_{2}}{d t^{2}} + 2 \frac{d^{2} θ_{3}}{d t^{2}} + \frac{d^{2} θ_{4}}{d t^{2}} + 4 \frac{g}{l} θ_{1} = 0 \\ 3 \frac{d^{2} θ_{1}}{d t^{2}} + 3 \frac{d^{2} θ_{2}}{d t^{2}} + 2 \frac{d^{2} θ_{3}}{d t^{2}} + \frac{d^{2} θ_{4}}{d t^{2}} + 3 \frac{g}{l} θ_{2} = 0 \\ 2 \frac{d^{2} θ_{1}}{d t^{2}} + 2 \frac{d^{2} θ_{2}}{d t^{2}} + 2 \frac{d^{2} θ_{3}}{d t^{2}} + \frac{d^{2} θ_{4}}{d t^{2}} + 2 \frac{g}{l} θ_{3} = 0 \\ \frac{d^{2} θ_{1}}{d t^{2}} + \frac{d^{2} θ_{2}}{d t^{2}} + \frac{d^{2} θ_{3}}{d t^{2}} + \frac{d^{2} θ_{4}}{d t^{2}} + \frac{g}{l} θ_{4} = 0 \end{cases}$

Vamos a calcular y representar los modos normales de vibración. Suponiendo una solución θ₁=A₁sin(ωt), θ₂=A₂sin(ωt), θ₃=A₃sin(ωt), θ₄=A₄sin(ωt) obtenemos el sistema de ecuaciones

${\begin{cases} 4 (\frac{g}{l} - ω^{2}) A_{1} - 3 ω^{2} A_{2} - 2 ω^{2} A_{3} - ω^{2} A_{4} = 0 \\ - 3 ω^{2} A_{1} + 3 (\frac{g}{l} - ω^{2}) A_{2} - 2 ω^{2} A_{3} - ω^{2} A_{4} = 0 \\ - 2 ω^{2} A_{1} - 2 ω^{2} A_{2} + 2 (\frac{g}{l} - ω^{2}) A_{3} - ω^{2} A_{4} = 0 \\ - ω^{2} A_{1} - ω^{2} A_{2} - ω^{2} A_{3} + (\frac{g}{l} - ω^{2}) A_{4} = 0 \end{cases}$

En este sistema homogéneo de cuatro ecuaciones con cuatro incógnitas, el determinante de los coeficientes ha de ser cero

$| \begin{matrix} 4 (\frac{g}{l} - ω^{2}) & - 3 ω^{2} & - 2 ω^{2} & - ω^{2} \\ - 3 ω^{2} & 3 (\frac{g}{l} - ω^{2}) & - 2 ω^{2} & - ω^{2} \\ - 2 ω^{2} & - 2 ω^{2} & 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & - ω^{2} & - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} | = 0$

Obtenemos la ecuación cuarto orden en ω². En el código x es ω² y g es g/l

>> syms g x;
>> A=[4*(g-x),-3*x,-2*x,-x;-3*x,3*(g-x),-2*x,-x;
-2*x,-2*x,2*(g-x),-x;-x,-x,-x,g-x];
>> det(A)
ans = 24*g^4 - 96*g^3*x + 72*g^2*x^2 - 16*g*x^3 + x^4

$ω^{8} - 16 \frac{g}{l} ω^{6} + 72 \frac{g^{2}}{l^{2}} ω^{4} - 96 \frac{g^{3}}{l^{3}} ω^{2} + 24 \frac{g^{4}}{l^{4}} = 0$

Los cuadrados de las frecuencias de los modos normales de vibración son las raíces de esta ecuación

>> n=4; %número de péndulos
>> L=1.12; %longitud total
>> roots([1, -16*9.8/(L/n),72*9.8^2/(L/n)^2,-96*9.8^3/(L/n)^3, 24*9.8^4/(L/n)^4])
ans =  328.8275
  158.7817
   61.1016
   11.2892

Tomamos la segunda, tercera y cuarta ecuación del sistema homogéneo de cuatro ecuaciones, para calcular las amplitudes A₂, A₃ y A₄ en términos de la amplitud A₁

$\begin{array}{l} {\begin{cases} 3 (\frac{g}{l} - ω^{2}) A_{2} - 2 ω^{2} A_{3} - ω^{2} A_{4} = 3 ω^{2} A_{1} \\ - 2 ω^{2} A_{2} + 2 (\frac{g}{l} - ω^{2}) A_{3} - ω^{2} A_{4} = 2 ω^{2} A_{1} \\ - ω^{2} A_{2} - ω^{2} A_{3} + (\frac{g}{l} - ω^{2}) A_{4} = ω^{2} A_{1} \end{cases} \\ A_{2} = \frac{| \begin{matrix} 3 & - 2 ω^{2} & - ω^{2} \\ 2 & 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ 1 & - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} |}{| \begin{matrix} 3 (\frac{g}{l} - ω^{2}) & - 2 ω^{2} & - ω^{2} \\ - 2 ω^{2} & 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} |} ω^{2} A_{1} = \frac{ω^{4} - 6 \frac{g}{l} ω^{2} + 6 \frac{g^{2}}{l^{2}}}{- ω^{6} + 9 \frac{g}{l} ω^{4} - 18 \frac{g^{2}}{l^{2}} ω^{2} + 6 \frac{g^{3}}{l^{3}}} ω^{2} A_{1} \\ A_{3} = \frac{| \begin{matrix} 3 (\frac{g}{l} - ω^{2}) & 3 & - ω^{2} \\ - 2 ω^{2} & 2 & - ω^{2} \\ - ω^{2} & 1 & (\frac{g}{l} - ω^{2}) \end{matrix} |}{| \begin{matrix} 3 (\frac{g}{l} - ω^{2}) & - 2 ω^{2} & - ω^{2} \\ - 2 ω^{2} & 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} |} ω^{2} A_{1} = \frac{- 3 \frac{g}{l} ω^{2} + 6 \frac{g^{2}}{l^{2}}}{- ω^{6} + 9 \frac{g}{l} ω^{4} - 18 \frac{g^{2}}{l^{2}} ω^{2} + 6 \frac{g^{3}}{l^{3}}} ω^{2} A_{1} \\ A_{4} = \frac{| \begin{matrix} 3 (\frac{g}{l} - ω^{2}) & - 2 ω^{2} & 3 \\ - 2 ω^{2} & 2 (\frac{g}{l} - ω^{2}) & 2 \\ - ω^{2} & - ω^{2} & 1 \end{matrix} |}{| \begin{matrix} 3 (\frac{g}{l} - ω^{2}) & - 2 ω^{2} & - ω^{2} \\ - 2 ω^{2} & 2 (\frac{g}{l} - ω^{2}) & - ω^{2} \\ - ω^{2} & - ω^{2} & (\frac{g}{l} - ω^{2}) \end{matrix} |} ω^{2} A_{1} = \frac{6 \frac{g^{2}}{l^{2}}}{- ω^{6} + 9 \frac{g}{l} ω^{4} - 18 \frac{g^{2}}{l^{2}} ω^{2} + 6 \frac{g^{3}}{l^{3}}} ω^{2} A_{1} \end{array}$

Calculamos los determinantes. En el código x es ω² y g es g/l

>> syms g x;
>> A = [3*(g - x),-2*x,-x;-2*x,2*(g - x), -x;-x,-x,g - x]; %denominador
>> det(A)
ans = 6*g^3 - 18*g^2*x + 9*g*x^2 - x^3
>> A = [3,2,1;-2*x,2*(g - x), -x;-x,-x,g - x]; %numerador A2
>> det(A)
ans = 6*g^2 - 6*g*x + x^2
>> A = [3*(g - x),-2*x,-x;3,2,1;-x,-x,g - x]; %numerador A3
>> det(A)
ans = 6*g^2 - 3*x*g
>> A = [3*(g - x),-2*x,-x;-2*x,2*(g - x), -x;3,2,1]; %numerador A4
>> det(A)
ans = 6*g^2

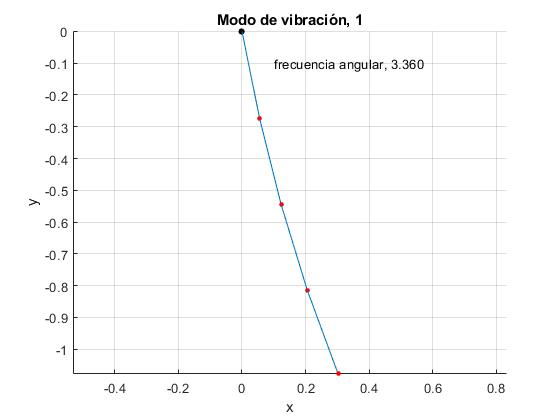
Calculamos A₂, A₃ y A₄ para el primer modo de vibración de frecuencia angular ω=ω₁. El ángulo θ₁ que forma el primer péndulo con la vertical será proporcional a A₁, el ángulo θ₂ que forma el segundo péndulo con la vertical será proporcional a A₂, el ángulo θ₃ que forma el tercer péndulo con la vertical será proporcional a A₃ y el ángulo θ₄ que forma el cuarto péndulo con la vertical será proporcional a A₄. Representamos el primer modo de vibración.

L=1.12; %longitud total
n=4; %número de péndulos
%cuadrado frecuencias ordenadas
w2=sort(roots([1, -16*9.8/(L/n),72*9.8^2/(L/n)^2,-96*9.8^3/(L/n)^3, 
24*9.8^4/(L/n)^4])); 
iModo=2; %modo de vibración
A1=0.2; %escala
den=-w2(iModo)^3+9*9.8/(L/n)*w2(iModo)^2-18*9.8^2/(L/n)^2*w2(iModo)+6*9.8^3/(L/n)^3;
A2=(w2(iModo)^2-6*9.8/(L/n)*w2(iModo)+6*9.8^2/(L/n)^2)*w2(iModo)*A1/den;
A3=(-3*9.8*w2(iModo)/(L/n)+6*9.8^2/(L/n)^2)*w2(iModo)*A1/den;
A4=6*9.8^2/(L/n)^2*w2(iModo)*A1/den;

angulos=[A1,A2,A3, A4];
hold on
x1=0; y1=0;
plot(x1,y1,'ko','markersize',4,'markerfacecolor','k')
for j=1:n
    x2=x1+(L/n)*sin(angulos(j));
    y2=y1-(L/n)*cos(angulos(j));
    line([x1,x2],[y1,y2])
    plot(x2,y2,'ro','markersize',3,'markerfacecolor','r')
    x1=x2;
    y1=y2;
end
text(0.1,-0.1, sprintf('frecuencia angular, %1.3f',sqrt(w2(iModo))))
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title(sprintf('Modo de vibración, %i',iModo))

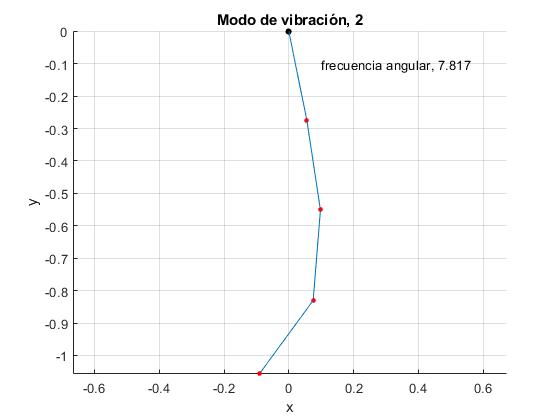
Repetimos para el segundo modo de vibración de frecuencia angular ω=ω₂, cambiando el valor de la variable iModo=2

n péndulos

Para n= 4 péndulos, escribimos el sistema de ecuaciones diferenciales en forma matricial

$\begin{array}{l} (\begin{matrix} (m_{1} + m_{2} + m_{3} + m_{4}) l_{1} & (m_{2} + m_{3} + m_{4}) l_{2} & (m_{3} + m_{4}) l_{3} & m_{4} l_{4} \\ (m_{2} + m_{3} + m_{4}) l_{1} & (m_{2} + m_{3} + m_{4}) l_{2} & (m_{3} + m_{4}) l_{3} & m_{4} l_{4} \\ (m_{3} + m_{4}) l_{1} & (m_{3} + m_{4}) l_{2} & (m_{3} + m_{4}) l_{3} & m_{4} l_{4} \\ m_{4} l_{1} & m_{4} l_{2} & m_{4} l_{3} & m_{4} l_{4} \end{matrix}) (\begin{matrix} \frac{d^{2} θ_{1}}{d t^{2}} \\ \frac{d^{2} θ_{2}}{d t^{2}} \\ \frac{d^{2} θ_{3}}{d t^{2}} \\ \frac{d^{2} θ_{4}}{d t^{2}} \end{matrix}) \\ + g (\begin{matrix} (m_{1} + m_{2} + m_{3} + m_{4}) & 0 & 0 & 0 \\ 0 & (m_{2} + m_{3} + m_{4}) & 0 & 0 \\ 0 & 0 & (m_{3} + m_{4}) & 0 \\ 0 & 0 & 0 & m_{4} \end{matrix}) (\begin{matrix} θ_{1} \\ θ_{2} \\ θ_{3} \\ θ_{4} \end{matrix}) = 0 \end{array}$

Para el caso particular, m₁=m₂=m₃=m₄=m, l₁=l₂=l₃=l₄=l

$(\begin{matrix} 4 & 3 & 2 & 1 \\ 3 & 3 & 2 & 1 \\ 2 & 2 & 2 & 1 \\ 1 & 1 & 1 & 1 \end{matrix}) (\begin{matrix} \frac{d^{2} θ_{1}}{d t^{2}} \\ \frac{d^{2} θ_{2}}{d t^{2}} \\ \frac{d^{2} θ_{3}}{d t^{2}} \\ \frac{d^{2} θ_{4}}{d t^{2}} \end{matrix}) + \frac{g}{l} (\begin{matrix} 4 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}) (\begin{matrix} θ_{1} \\ θ_{2} \\ θ_{3} \\ θ_{4} \end{matrix}) = 0$

Ahora, es fácil generalizar para n péndulos acoplados

$\begin{array}{l} (\begin{matrix} n & n - 1 & n - 2 & ... & 1 \\ n - 1 & n - 1 & n - 2 & ... & 1 \\ n - 2 & n - 2 & n - 2 & ... & 1 \\ ... & ... & ... & ... & ... \\ 1 & 1 & 1 & 1 & 1 \end{matrix}) (\begin{matrix} \frac{d^{2} θ_{1}}{d t^{2}} \\ \frac{d^{2} θ_{2}}{d t^{2}} \\ \frac{d^{2} θ_{3}}{d t^{2}} \\ ... \\ \frac{d^{2} θ_{n}}{d t^{2}} \end{matrix}) + \frac{g}{l} (\begin{matrix} n & 0 & 0 & ... & 0 \\ 0 & n - 1 & 0 & ... & 0 \\ 0 & 0 & n - 2 & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & 0 & 0 & ... & 1 \end{matrix}) (\begin{matrix} θ_{1} \\ θ_{2} \\ θ_{3} \\ ... \\ θ_{n} \end{matrix}) = 0 \\ M \frac{d^{2} x}{d t^{2}} + K x = 0 \end{array}$

Valores propios

Se calculan las frecuencias de los modos normales de vibración resolviendo el sistema homogéneo

$\begin{array}{l} \begin{array}{l} - ω^{2} M \cdot x + K \cdot x = 0 \\ (K - ω^{2} M) \cdot x = 0 \end{array} \\ (M^{- 1} K - ω^{2} I) x = 0 \end{array}$

Los valores propios de la matriz M^-1·K son los cuadrados de las frecuencias ω² de los modos normales de vibración

Para n=4 péndulos de longitud total L=1.12 m

L=1.12; %longitud total
n=4; %número de péndulos
M=zeros(n,n);
for i=1:n
    for j=1:i-1
        M(i,j)=n-i+1;
   end
   for j=i:n
       M(i,j)=n+1-j;
   end
end
K=diag(n:-1:1)*9.8/(L/n);
[V,D]=eig(K/M);
w2=sort(diag(D)); %vector de frecuencias propias al cuadrado, ordenados

El cuadrado de las frecuencias de los modos normales de vibración, coinciden con las calculadas en el apartado anterior

>>w2
ans =
   11.2892
   61.1016
  158.7817
  328.8275

Tomamos la segunda, tercera ... n ecuación del sistema homogéneo de n ecuaciones, para calcular las amplitudes A₂, A₃ ... A_n en términos de la amplitud A₁. En forma matricial se escribe para n=4, que es fácil generalizar para cualquier n

${- ω^{2} (\begin{matrix} 3 & 2 & 1 \\ 2 & 2 & 1 \\ 1 & 1 & 1 \end{matrix}) + \frac{g}{l} (\begin{matrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{matrix})} (\begin{matrix} A_{2} \\ A_{3} \\ A_{4} \end{matrix}) = ω^{2} (\begin{matrix} 3 \\ 2 \\ 1 \end{matrix}) A_{1}$

La primera matriz es la submatriz de M de 3×3 inferior derecha. Añadimos estas líneas de código para calcular los coeficienets A₂, A₃ y A₄

....
A=zeros(n-1);
for i=1:length(w2)
    C=-w2(i)*M(2:n,2:n)+(9.8/(L/n))*diag(n-1:-1:1); %incógnitas
    D=w2(i)*(n-1:-1:1)'; %términos independientes
    for j=1:n-1
        num=C;
        num(1:end,j)=D;
        A(i,j)=det(num)/det(C);
    end
end
....

>> A
A =
    1.2258    1.4798    1.7643   %A2, A3 y A4 para el primer modo w1
    0.7514   -0.4017   -3.1597   %A2, A3 y A4 para el segundo modo w2
   -0.1789   -2.1309    1.6801   %A2, A3 y A4 para el tercer modo w3
   -1.7984    1.0528   -0.2847   %A2, A3 y A4 para el cuarto modo w4

El ángulo θ₁ que forma el primer péndulo con la vertical será proporcional a A₁, el ángulo θ₂ que forma el segundo péndulo con la vertical será proporcional a A₂,... el ángulo θ_n que forma el péndulo n con la vertical será proporcional a A_n . Representamos el primer modo de vibración para n=8 péndulos. El código completo es

L=1.12; %longitud total
n=4; %número de péndulos
M=zeros(n,n);
for i=1:n
    for j=1:i-1
        M(i,j)=n-i+1;
   end
   for j=i:n
       M(i,j)=n+1-j;
   end
end
K=diag(n:-1:1)*9.8/(L/n);
[V,D]=eig(K/M);
w2=sort(diag(D)); %vector de frecuencias propias al cuadrado, ordenados

%cálculo de los coeficientes A2, A3, A4...
A=zeros(n-1);
for i=1:length(w2)
    C=-w2(i)*M(2:n,2:n)+(9.8/(L/n))*diag(n-1:-1:1); %incógnitas
    D=w2(i)*(n-1:-1:1)'; %términos independientes
    for j=1:n-1
        num=C;
        num(1:end,j)=D;
        A(i,j)=det(num)/det(C);
    end
end

hold on
plot(0,0,'ko','markersize',4,'markerfacecolor','k')
A1=0.2; %escala
iModo=2; %modo normal de vibración
angulos=[A1,A(iModo,1:end)*A1];
x1=0; y1=0;
for j=1:n
    x2=x1+(L/n)*sin(angulos(j));
    y2=y1-(L/n)*cos(angulos(j));
    line([x1,x2],[y1,y2])
    plot(x2,y2,'ro','markersize',3,'markerfacecolor','r')
    x1=x2;
    y1=y2;
end
text(0.1,-0.1, sprintf('frecuencia angular, %1.3f',sqrt(w2(iModo))))
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title(sprintf('Modo de vibración, %i',iModo))

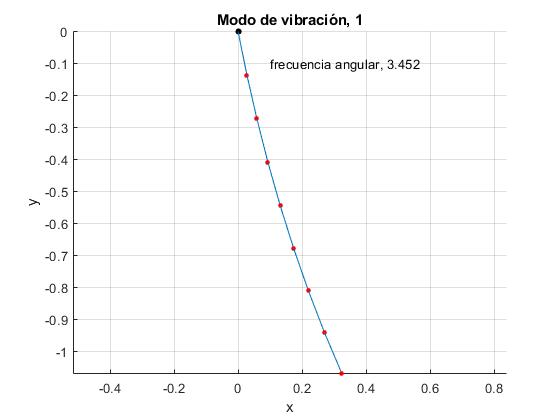
Repetimos para el segundo modo de vibración de frecuencia angular ω=ω₂, cambiando el valor de la variable iModo=2

Péndulo simple, n péndulos y péndulo compuesto de la misma longitud

Creamos un script para representar

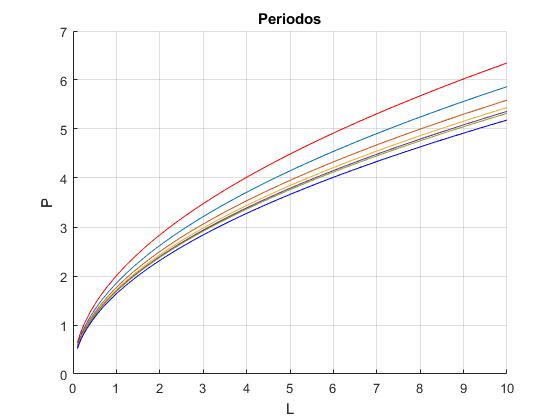
El periodo de un péndulo simple en función de la longitud L (en color rojo)

$P = 2 π \sqrt{\frac{L}{g}}$

El periodo de un péndulo compuesto, una varilla de masa m y longitud L cuyo punto de suspensión se encuentra en un extremo (en color azul)

$P = 2 π \sqrt{\frac{\frac{1}{12} m L^{2} + m {(\frac{L}{2})}^{2}}{m g (\frac{L}{2})}} = 2 π \sqrt{\frac{2}{3} \frac{L}{g}}$

Si L es la longitud total de los n péndulos acoplados, si la frecuencia del modo fundamental ω_n1. El periodo que nos interesa es

$P_{n} = \frac{2 π}{ω_{n 1}}$

Se representan los periodos de los sistemas formados por 2, 4, 8, 16 y 32 péndulos acoplados en función de la longitud total L de los péndulos. Estos periodos están comprendidos entre los de un pendulo simple (rojo) y de un péndulo compuesto (azul) tal como se aprecia en la figura

LL=0.1:0.1:10;
P=zeros(1, length(LL));
hold on
for n=[2,4,8,16,32]
    M=zeros(n,n);
    for i=1:n
        for j=1:i-1
            M(i,j)=n-i+1;
        end
        for j=i:n
            M(i,j)=n+1-j;
        end
    end
    m=1;
     for L=LL
        K=diag(n:-1:1)*9.8/(L/n);
        [V,D]=eig(K/M);
        w2=min(diag(D));
        P(m)=2*pi/sqrt(w2);
        m=m+1;
    end
    plot(LL,P)
end
fplot(@(x) 2*pi./sqrt(9.8./x),[0.1,10],'color','r')
fplot(@(x) 2*pi*sqrt(2/3)./sqrt(9.8./x),[0.1,10],'color','b')
hold off
grid on
xlabel('L')
ylabel('P')
title('Periodos')

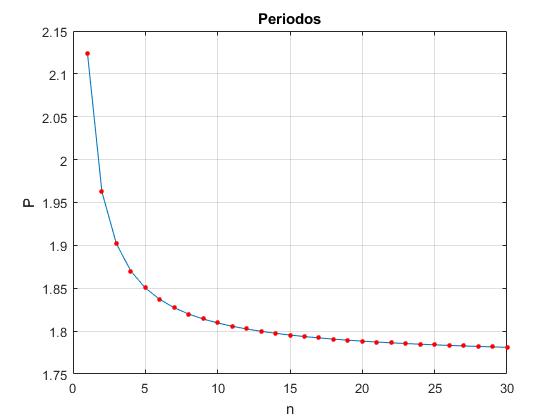
La longitud total de los péndulos acoplados no cambia

Sea L=1.12 m la longitud total de los péndulos acoplados. Representamos el periodo P_n en función del número n de péndulos

L=1.12; %longitud total
P=zeros(1,30);
P(1)=2*pi/sqrt(9.8/L);
for n=2:30 %número de péndulos
    M=zeros(n,n);
    for i=1:n
        for j=1:i-1
            M(i,j)=n-i+1;
        end
        for j=i:n
            M(i,j)=n+1-j;
        end
    end
    K=diag(n:-1:1)*9.8/(L/n);
    [V,D]=eig(K/M);
    w2=min(diag(D));
    P(n)=2*pi/sqrt(w2);
end
plot(1:30,P,'-o','markersize',3,'markeredgecolor','r','markerfacecolor','r')    
grid on
xlabel('n')
ylabel('P')
title('Periodos')

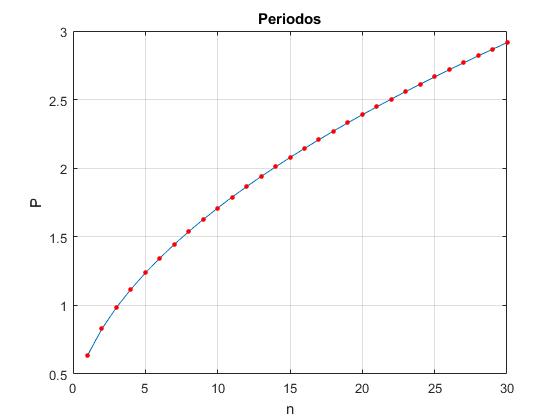
La densidad n/L de los péndulos acoplados no cambia

Para que la densidad no cambie, la longitud total L de los péndulos acoplados será proporcional al número n de péndulos. Sea n/L=10

P=zeros(1,30);
rho=10; %densidad n/L
P(1)=2*pi/sqrt(9.8*rho);
for n=2:30 %número de péndulos
    M=zeros(n,n);
    for i=1:n
        for j=1:i-1
            M(i,j)=n-i+1;
        end
        for j=i:n
            M(i,j)=n+1-j;
        end
    end
    K=diag(n:-1:1)*9.8*rho;
    [V,D]=eig(K/M);
    w2=min(diag(D));
    P(n)=2*pi/sqrt(w2);
end
plot(1:30,P,'-o','markersize',3,'markeredgecolor','r','markerfacecolor','r')    
grid on
xlabel('n')
ylabel('P')
title('Periodos')

Referencias

J. C. Zamora, F. Fajardo, J. Alexis Rodríguez. Oscillator experiments with periods between the simple pendulum and the rigid rod. Am. J. Phys. 77 (2) February 2009, pp. 169-172