Oscilaciones acopladas de un péndulo y un muelle elástico
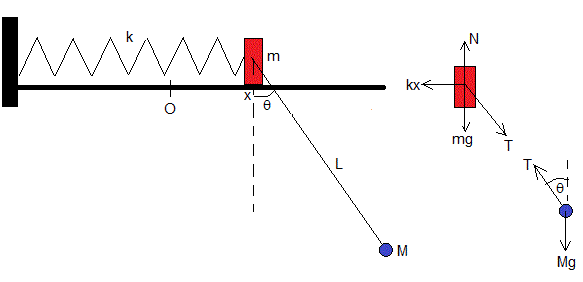
En la figura, se muestra los dos cuerpos y las fuerzas que actúan sobre los mismos.
Ecuaciones del movimiento
La posición del bloque de masa m es x. La posición de la masa puntual M es
xp=x+lsinθ
yp=lcosθ
Derivamos para obtener la velocidad de la masa puntual M
Volvemos a derivar para obtener la aceleración
Aplicamos la segunda ley de Newton para describir el movimiento del bloque de masa m a lo largo del eje X
El movimiento de la masa puntual M a lo largo del eje X y del eje Y es
Las tres ecuaciones que describen el movimiento del sistema formado por el bloque y la masa puntual, son
Eliminamos la variable desconocida T, la tensión de la cuerda. Sumamos la primera y la segunda ecuación. Multiplicamos la segunda ecuación por cosθ y la tercera por sinθ y las sumamos. Obteniendo un sistema de dos ecuaciones diferenciales en x y θ.
Formulación de Lagrange
Disponemos de otro modo alternativo de obtener las ecuaciones del movimiento. La energía cinética del sistema es
La energía potencial es la suma de la energía potencial gravitatoria de la masa puntual M y la energía potencial elástica del muelle deformado x
La Lagrangiana en términos de las coordenadas x y θ es
La ecuación de Euler-Lagrange para x es
La ecuación de Euler-Lagrange para θ es
Llegamos por dos caminos distintos a las mismas ecuaciones
Solución numérica de las ecuaciones del movimiento
Para resolver este sistema de ecuaciones diferenciales, cada una de las dos ecuaciones solamente puede tener una única derivada segunda. Despejamos d2x/dt2 en la primera ecuación y la sustituimos en la segunda
Elaboramos un script con los siguientes valores de los parámetros que podremos modificar: masa del bloque m=1.5 kg, masa puntual M=0.5 kg, constante del muelle k=20 N/m, longitud de la cuerda L=0.7 m. A continuación, las condiciones iniciales: posición del bloque x=0.3, velocidad incial dx/dt=0. Desplazamiento angular inicial del péndulo θ=π/6, velocidad angular inicial dθ/dt=0.
Se resuelve el sistema de ecuaciones diferenciales mediante el procedimiento ode45, durante un tiempo de 10 s. Se representa la posición del bloque x y la posición angular del péndulo θ en función del tiempo t.
m=1.5; %bloque
M=0.5; %masa puntual, péndulo
k=20; %constante del muelle
L=0.7; %longitud del péndulo
%x0=[0, 0, pi/6,0]; %ejemplos de condiciones iniciales
%x0=[0.1, 0.1, pi/6,pi/20];
x0=[0.3, 0, pi/4,0]; %condiciones iniciales
tspan=[0,10];
% x(1)=x, x(2)=dx/dt, x(3)=theta; x(4)=dtheta/dt
fg=@(t,x)[x(2);(M*L*sin(x(3))*x(4)^2-k*x(1)+M*9.8*sin(x(3))*cos(x(3)))
/(M*sin(x(3))^2+m);
x(4); -(M*sin(x(3))*cos(x(3))*x(4)^2-k*x(1)*cos(x(3))
/L+(m+M)*9.8*sin(x(3))/L)/(M*sin(x(3))^2+m)];
[t,x]=ode45(fg,tspan,x0);
hold on
plot(t,x(:,1))
plot(t,x(:,3))
%plot(t,x(:,2))
%plot(t,x(:,4))
hold off
grid on
legend('bloque','péndulo');
xlabel('t')
ylabel('x, \theta')
title('Bloque y péndulo')
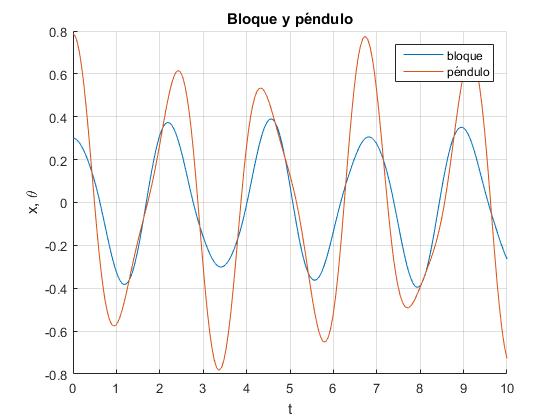
Comprobamos que la energía total E=T+U es constante
>> E=(m+M)*x(:,2).^2/2+M*L*cos(x(:,3)).*(x(:,2).*x(:,4)-9.8)+ M*L^2*x(:,4).^2/2+k*x(:,1).^2/2 E =-1.5254 -1.5254 -1.5254 -1.5254 -1.5254 ...
Actividades
En primer lugar, especificamos los parámetros del sistema
- La masa m del bloque en el control titulado Masas: bloque
- La masa M de la masa puntual en el control titulado Masas: péndulo
- La constante elástica k del muelle en el control titulado constante
- La longitud l de la cuerda que sujeta la masa puntual en el control titulado longitud
En segundo lugar, especificamos las condiciones iniciales
- La posición inicial x del bloque en el control titulado Posición bloque
- La posición angular inicial en grados θ del péndulo en el control titulado Angulo péndulo
- El bloque y la masa puntual parten del reposo. La velocidades iniciales del bloque dx/dt=0 y la velocidad angular del péndulo dθ/dt=0
Si queremos ver las gráficas de la posición x del bloque (en color rojo) y la posición angular θ del péndulo (en color azul), activamos la casilla titulada Gráfica
Se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento de Runge-Kutta. El programa calcula la energía del sistema E en cada instante y lo compara con la energía inicial E0. Si la desviación es mayor que el 1% el programa se detiene.
Aproximaciones
Si nos restringimos a pequeños valores de los ángulos θ, las ecuaciones del movimiento se hacen mucho más simples. Aproximamos, sinθ≈θ. Desarrollamos en serie de Taylor cosθ y tomamos los dos primeros términos no nulos del desarrollo en serie
La energía cinética, potencial y la lagrangiana L=T-U con esta aproximación, se expresa
Con esta aproximación, la ecuación de Euler-Lagrange para x es
y la ecuación de Euler-Lagrange para θ es
Despejamos las derivadas segundas de x y de θ en el sistema de las dos ecuaciones
Buscamos una solución de la forma
x=Xsin(ωt+φ), θ=Θsin(ωt+φ)
que representa MAS de amplitud X, Θ y frecuencia angular ω.
Tenemos un sistema homogéneo, los cuadrados de las frecuencias de los modos normales de vibración se calculan haciendo que el determinante de los coeficientes sea igual a cero
Obtenemos una ecuación de segundo grado en ω2 con dos raíces positivas, ω1 y ω2.
La forma general de la posición del bloque x en función del tiempo t es una combinación de los dos modos normales de vibración
x(t)=A1sin(ω1t)+ B1cos(ω1t)+ C1sin(ω2t)+ D1cos(ω2t)
Lo mismo para θ
θ(t)=A2sin(ω1t)+ B2cos(ω1t)+ C2sin(ω2t)+ D2cos(ω2t)
Las velocidades son
Relacionamos los coeficientes A1 y A2, B1 y B2, C1 y C2, D1 y D2, a través de una de las dos ecuaciones diferenciales del movimiento
Tenemos cuatro relaciones
Las condiciones iniciales determinan los valores de los cuatro coeficientes A1, B1, C1 y D1 y por tanto, de los coeficientes A2, B2, C2 y D2, a través de las relaciones establecidas anteriormente.
Desplazamos el bloque x0 y el péndulo un ángulo θ0 a continuación, los soltamos. La velocidad inicial es dx/dt=0, dθ/dt=0 en el instante t=0.
Resolvemos el sistema de cuatro ecuaciones junto a las relaciones establecidas anteriormente.
x0=B1+D1
0=ω1·A1+ ω2·C1
θ0=B2+D2
0=ω1·A2+ ω2·C2
La solución de este sistema es
A1=C1=A2=C2=0
La posición angular en función del tiempo t de cada una de las partículas es
x(t)=B1cos(ω1t)+D1cos(ω2t)
θ(t)=B2cos(ω1t)+D2cos(ω2t)
Modos normales de vibración
Para comprobar los modos normales en la simulación, vamos a establecer los siguientes valores para los parámetros: Masa del bloque m=1.5 kg, masa puntual del péndulo M=0.5 kg, constante del muelle k=20 N/m, longitud del péndulo l=0.7 m. El desplazamiento angular inicial del péndulo es de 30°=π/6. El script nos calcula el desplazamiento inicial del bloque x0 que introducimos con los datos anteriores en el programa interactivo
m=1.5; %bloque
M=0.5; %péndulo
k=20; %constante del muelle
L=0.7; %longitud del péndulo
%condiciones iniciales
fi0=pi/6; %desviación inicialdel péndulo
%cuadrado d elas frecuencias w_1 y w_2
a=m^2*L;
b=(m+M)*9.8*m+k*L*m;
c=m*9.8*k;
w2_1=(b+sqrt(b^2-4*a*c))/(2*a);
w2_2=(b-sqrt(b^2-4*a*c))/(2*a);
%primer modo de vibración
x0=M*9.8*fi0/(k-m*w2_1);
B1=(M*9.8*fi0-(k-m*w2_2)*x0)/(m*(w2_2-w2_1));
B2=(k-m*w2_1)*B1/(M*9.8);
D1=(-M*9.8*fi0+(k-m*w2_1)*x0)/(m*(w2_2-w2_1));
D2=(k-m*w2_2)*D1/(M*9.8);
x=@(t) B1*cos(sqrt(w2_1)*t)+D1*cos(sqrt(w2_2)*t);
theta=@(t) B2*cos(sqrt(w2_1)*t)+D2*cos(sqrt(w2_2)*t);
hold on
fplot(x,[0,10])
fplot(theta,[0,10])
hold off
grid on
legend('bloque','péndulo');
xlabel('t')
ylabel('x, \theta')
title('Bloque y péndulo')
-
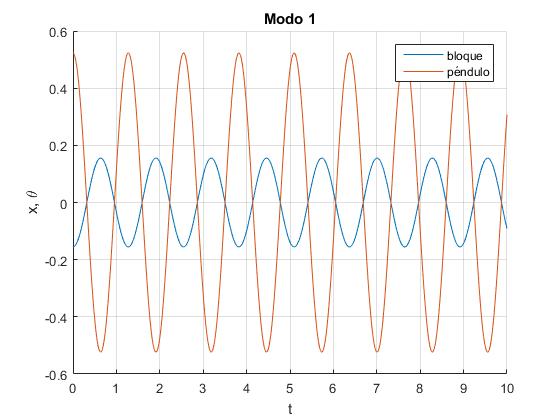
El modo 1 de frecuencia angular ω1, se obtiene cuando D2=0, entonces D1=0, la relación entre las posciones iniciales x0 y θ0 es
La posición angular en función del tiempo t de cada una de las partículas es
Resultados:
La frecuencia angular del primer modo de vibración es ω1=4.9322. El desplazamiento inicial del bloque x0=-0.1556. Las amplitudes B1=-0.1556 y B2=0.5236
>> B1,B2,D1,D2 B1 = -0.1556 B2 = 0.5236 D1 = 0 D2 = 0 >> sqrt(w2_1) ans = 4.9322 >> x0 x0 = -0.1556
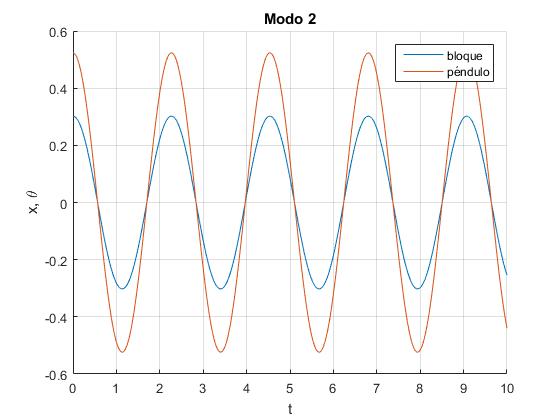
El modo 2 de frecuencia angular ω2, se obtiene cuando B2=0, entonces B1=0, la relación entre las posciones iniciales x0 y θ0 es
La posición angular en función del tiempo t de cada una de las partículas es
Cambiamos una línea en el script para establecer el segundo modo de vibración
.... w2_1=(b+sqrt(b^2-4*a*c))/(2*a); w2_2=(b-sqrt(b^2-4*a*c))/(2*a); %segundo modo de vibración x0=M*9.8*fi0/(k-m*w2_2); ....
Resultados:
La frecuencia angular del segundo modo de vibración es ω2=2.7701. El desplazamiento inicial del bloque x0=0.3022. Las amplitudes D1=0.3022 y D2=0.5236
>> B1,B2,D1,D2 B1 = 0 B2 = 0 D1 = 0.3022 D2 = 0.5236 >> sqrt(w2_2) ans = 2.7701 >> x0 x0 = 0.3022