Modos normales de vibración de sistemas lineales homogéneos.

Modos normales de vibración de sistemas lineales homogéneos

Los sistemas que analizamos en esta página, están compuestos por masas puntuales unidas a muelles elásticos de masa despreciable. Cada elemento está situado entre dos puntos. El estado de cada punto está definido por un vector columna que especifica su desplazamiento y por la fuerza interna que actúa. Una matriz cuadrada de 2×2 relaciona dos puntos consecutivos del sistema.

Muelle elástico

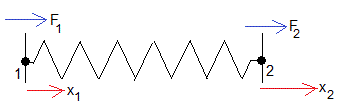
Un muelle elástico de constante k une los puntos 1 y 2. Las fuerzas en ambos puntos son iguales F₁=F₂. La deformación del muelle, es x₂-x₁

$\begin{array}{l} F_{1} = k (x_{2} - x_{1}) \\ x_{2} = x_{1} + \frac{F_{1}}{k} \end{array}$

Relacionamos x₂ y F₂ con x₁ y F₁ mediante una matriz 2×2

$(\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix})$

Denominaremos a esta matriz T_s

El vector columna de la izquierda es el estado del punto 2 y el de la derecha, el estado del punto 1. La matriz 2×2 relaciona los estados de dos puntos unidos por un elemento, en este caso el muelle

Partícula

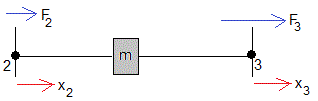
Una partícula tiene la misma posición x₂=x₃. La fuerza neta que actúa sobre la partícula F₃-F₂ es igual al producto de su masa m por la aceleración

$F_{3} - F_{2} = m \frac{d^{2} x_{2}}{d t^{2}}$

Si la partícula describe un Movimiento Armónico Simple de frecuencia angular ω, la aceleración es proporcional al desplazamiento y de sentido contrario a éste, -ω²x₂.

$F_{3} - F_{2} = - m ω^{2} x_{2}$

Relacionamos el estado del punto 3, el vector columna (x₃; F₃) con el estado del punto 2, el vector columna (x₂; F₂) mediante una matriz 2×2

$(\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2} \\ F_{2} \end{matrix})$

Denominaremos a esta matriz T_p

Una vez que hemos definido el concepto de estado y las matrices que relacionan el estado de dos puntos consecutivos que se unen mediante un muelle o una partícula, vamos a ver como se aplican a los sistemas que se estudian en la sección de osciladores acoplados del capítulo Oscilaciones

Partícula unida a un muelle elástico

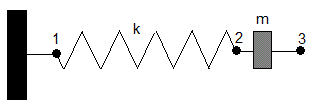
El sistema más sencillo está formado por una partícula de masa m unida a un muelle elástico de constante k

Relacionamos los estados de los puntos 1, 2 y 3 de la siguiente manera:

Entre los puntos 1 y 2 hay un muelle elástico de constante k, relacionamos el estado del punto 2 con el estado del punto 1

$(\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix})$

Entre los puntos 2 y 3 hay una partícula de masa m, relacionamos el estado del punto 3 con el estado del punto 2.

$(\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2} \\ F_{2} \end{matrix})$

Relacionamos el estado del punto 3 con el estado del punto 1

$\begin{array}{l} (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ - m ω^{2} & 1 - m ω^{2} / k \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \end{array}$

El producto de las matrices T_p·T_s da lugar a una matriz cuyo determinante es la unidad

Condiciones de contorno

Las condiciones de contorno son:

x₁=0, ya que el punto 1 es fijo
F₃=0, ya que el extremo 3 es libre

$(\begin{matrix} x_{3} \\ 0 \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ - m ω^{2} & 1 - \frac{m ω^{2}}{k} \end{matrix}) (\begin{matrix} 0 \\ F_{1} \end{matrix})$

Lo que implica que

$\begin{array}{l} x_{3} = \frac{F_{1}}{k} \\ 0 = (1 - \frac{m ω^{2}}{k}) F_{1} \end{array}$

x₃ es la deformación del muelle. El término entre paréntesis deberá ser cero, es decir, el resultado esperado, la frecuencia angular ω del MAS que describe una partícula de masa m unida a un muelle de constante k

$ω = \sqrt{\frac{k}{m}}$

Dos osciladores

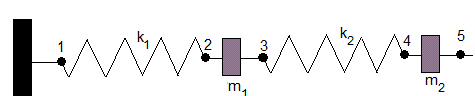
Consideremos el sistema de la figura: el primer oscilador está formado por un muelle de constante k₁, unido a una partícula de masa m₁, el otro extremo del muelle (punto 1) está fijo. El segundo oscilador está formado por un muelle de constante k₂, unido a una partícula de masa m₂, el otro extremo del muelle (punto 3) está unido a la partícula de masa m₁

Relacionamos los estados de los puntos 2-1 (muelle de constante k₁), 3-2(partícula de masa m₁), 4-3 (muelle de constante k₂), 5-4 (partícula de masa m₂). Finalmente, relacionamos los estados de los puntos extremos 5-1

$\begin{array}{l} (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{4} \\ F_{4} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{5} \\ F_{5} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{2} ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{4} \\ F_{4} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{2} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{5} \\ F_{5} \end{matrix}) = (\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \end{array}$

Condiciones de contorno

Las condiciones de contorno son:

x₁=0, ya que el punto 1 es fijo
F₅=0, ya que el extremo 5 es libre

$(\begin{matrix} x_{5} \\ 0 \end{matrix}) = (\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}) (\begin{matrix} 0 \\ F_{1} \end{matrix})$

Lo que implica que el elemento de la matriz T₂₂=0

En la página titulada Dos osciladores acoplados verticales calculamos las frecuencias de los modos normales de vibración del sistema formado por dos partículas de masas m₁=2m y m₂=m unidas a muelles elásticos de constante k₁=k₂=k

Frecuencias de los modos normales de oscilación

Utilizamos Math Symbolic de Matlab para realizar la multiplicación de matrices

syms k m w;
Ts_1=[1,1/k;0,1];
Tp_1=[1,0;-2*m*w^2,1];
Ts_2=[1,1/k;0,1];
Tp_2=[1,0;-m*w^2,1];

T=Tp_2*Ts_2*Tp_1*Ts_1;

Comprobamos que el determinante de la matriz T es la unidad

>> det(T)
ans =1

Utilizamos la función solve de MATLAB para calcular las raíces positivas de la ecuación T₂₂=0.

>> solve(T(2,2))
 ans =
 -(-(k*(2^(1/2) - 2))/(2*m))^(1/2)
  -((k*(2^(1/2) + 2))/(2*m))^(1/2)
  (-(k*(2^(1/2) - 2))/(2*m))^(1/2)
   ((k*(2^(1/2) + 2))/(2*m))^(1/2)

$ω_{1} = \sqrt{\frac{k}{m} (1 - \frac{\sqrt{2}}{2})} ω_{2} = \sqrt{\frac{k}{m} (1 + \frac{\sqrt{2}}{2})}$

Amplitudes del MAS que describe de cada una de las partículas

La amplitud de la primera partícula es x₂=x₃
La amplitud de la segunda partícula es x₄=x₅

Calculamos x₃ y x₅ cuando el sistema oscila en el primer modo normal de frecuencia ω₁, sabiendo que x₁=0

En el apatado anterior, hemos deducido la relación entre el estado del punto 3 y el estado del punto 1 y la relación entre el estado del punto 5 y del punto 1. Teniendo en cuenta las condiciones de contorno x₁=0, y asignando un valor arbitrario a F₁=1. Las expresiones de x₃ y x₅ son, respectivamente

$\begin{array}{l} x_{3} = (\begin{matrix} 1 & 0 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} 0 \\ 1 \end{matrix}) \\ x_{5} = (\begin{matrix} 1 & 0 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{2} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} 0 \\ 1 \end{matrix}) \end{array}$

Utilizamos MATLAB para calcular x₃ y x₅ para el primer modo normal de vibración, para el ejemplo de sistema descrito en este apartado, asignado los valores a la constante k=1 y a la masa m=1. Añadimos el siguiente código al script anterior

...
w1=subs((-(k*(-2^(1/2) - 2))/(2*m))^(1/2),{k,m},{1,1});
Vs_1=subs(Ts_1,k,1);
Vp_1=subs(Tp_1,{m,w},{1,w1});
Vs_2=subs(Ts_2,k,1);
Vp_2=subs(Tp_2,{m,w},{1,w1});

x5=[1,0]*(Vp_2*Vs_2*Vp_1*Vs_1)*[0;1];
x3=[1,0]*(Vp_1*Vs_1)*[0;1];
disp([double(x3), double(x5)])

    1.0000   1.4142

Como podemos ver en las figuras al final de la página Dos osciladores acoplados verticales, para la frecuencia ω₁=0.5412, las partículas oscilan en fase, y sus amplitudes están en la relación, x₅ es $\sqrt{2} = 1.4142...$ , veces la amplitud x₃

...
w2=subs(((k*(2^(1/2) + 2))/(2*m))^(1/2),{k,m},{1,1});
Vs_1=subs(Ts_1,k,1);
Vp_1=subs(Tp_1,{m,w},{1,w2});
Vs_2=subs(Ts_2,k,1);
Vp_2=subs(Tp_2,{m,w},{1,w2});

x5=[1,0]*(Vp_2*Vs_2*Vp_1*Vs_1)*[0;1];
x3=[1,0]*(Vp_1*Vs_1)*[0;1];
disp([double(x3), double(x5)])

    1.0000   -1.4142

Para el segundo modo de frecuencia ω₂=1.3066, los osciladores están en oposición de fase, la relación de amplitudes es la misma que para la frecuencia anterior

Dos osciladores acoplados

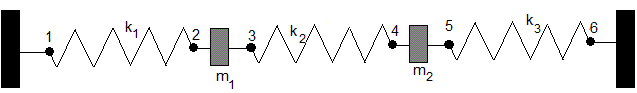
Consideremos el sistema de dos osciladores: el primero está formado por un muelle de constante k₁, unido a una partícula de masa m₁, el otro extremo del muelle (punto 1) está fijo. El segundo oscilador está formado por un muelle de constante k₃, unido a una partícula de masa m₂, el otro extremo del muelle (punto 6) está fijo. Las dos partículas están unidas por un muelle de constante k₂

Relacionamos los estados de los puntos 2-1 (muelle de constante k₁), 3-2(partícula de masa m₁), 4-3 (muelle de constante k₂), 5-4 (partícula de masa m₂), 6-5 (muelle de constante k₃). Finalmente, relacionamos los estados de los puntos extremos 6-1

$\begin{array}{l} (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{4} \\ F_{4} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{5} \\ F_{5} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{2} ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{4} \\ F_{4} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m_{2} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{6} \\ F_{6} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{3} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{5} \\ F_{5} \end{matrix}) = (\begin{matrix} 1 & 1 / k_{3} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{2} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{2} \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m_{1} ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k_{1} \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{6} \\ F_{6} \end{matrix}) = (\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \end{array}$

Condiciones de contorno

Las condiciones de contorno son:

x₁=0, ya que el punto 1 es fijo
x₆=0, ya que el extremo 6 es fijo

$\begin{array}{l} (\begin{matrix} 0 \\ F_{6} \end{matrix}) = (\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}) (\begin{matrix} 0 \\ F_{1} \end{matrix}) \\ \begin{array}{l} T_{12} F_{1} = 0 \\ F_{6} = T_{22} F_{1} \end{array}} T_{12} = 0 \end{array}$

Lo que implica que el elemento de la matriz T₁₂=0

En la página titulada Dos osciladores acoplados calculamos las frecuencias de los modos normales de vibración del sistema formado por dos partículas de masas m₁=m₂=m unidas a muelles elásticos de constante k₁=k₃=k, la constante del muelle que une las partículas es k₂=K

Frecuencias de los modos normales de oscilación

Utilizamos Math Symbolic de Matlab para realizar la multiplicación de matrices

syms k m w K;
Ts_1=[1,1/k;0,1];
Tp_1=[1,0;-m*w^2,1];
Ts_2=[1,1/K;0,1];
Tp_2=[1,0;-m*w^2,1];
Ts_3=[1,1/k;0,1];

T=Ts_3*Tp_2*Ts_2*Tp_1*Ts_1;

Comprobamos que el determinante de la matriz T es la unidad

>> det(T)
ans =1

Utilizamos la función solve para calcular las raíces positivas de la ecuación T₁₂=0.

>> solve(T(1,2))
ans =
  (m*(2*K + k))^(1/2)/m
 -(m*(2*K + k))^(1/2)/m
  (k^2*(m/k^3)^(1/2))/m
 -(k^2*(m/k^3)^(1/2))/m

$ω_{1} = \sqrt{\frac{k}{m}} ω_{2} = \sqrt{\frac{k + 2 K}{m}}$

Amplitudes del MAS que describe de cada una de las partículas

La amplitud de la primera partícula es x₂=x₃
La amplitud de la segunda partícula es x₄=x₅

Calculamos x₃ y x₅ cuando el sistema oscila en el primer modo normal de frecuencia ω₁, sabiendo que x₁=0

Utilizamos MATLAB para calcular x₃ y x₅ para el primer modo normal de vibración, para el ejemplo de sistema descrito en este apartado, asignado los valores a la constante k=10 y a la constante K=0.5 a las masas de las partículas m=1. Añadimos el siguiente código al script anterior

...
w1=subs(sqrt(k/m),{k,m},{10,1});
Vs_1=subs(Ts_1,k,10);
Vp_1=subs(Tp_1,{m,w},{1,w1});
Vs_2=subs(Ts_2,K,0.5);
Vp_2=subs(Tp_2,{m,w},{1,w1});

x5=[1,0]*(Vp_2*Vs_2*Vp_1*Vs_1)*[0;1];
x3=[1,0]*(Vp_1*Vs_1)*[0;1];
disp([double(x3), double(x5)])

   0.1000    0.1000

Como podemos ver en el programa interactivo o utilizando el código MATLAB al final de la página Dos osciladores acoplados, para la frecuencia ω₁=3.1623, las partículas oscilan en fase y sus amplitudes x₃=x₅ son las mismas

...
w1=subs(sqrt((k+2*K)/m),{k,K,m},{10,0.5,1});
Vs_1=subs(Ts_1,k,10);
Vp_1=subs(Tp_1,{m,w},{1,w1});
Vs_2=subs(Ts_2,K,0.5);
Vp_2=subs(Tp_2,{m,w},{1,w1});

x5=[1,0]*(Vp_2*Vs_2*Vp_1*Vs_1)*[0;1];
x3=[1,0]*(Vp_1*Vs_1)*[0;1];
disp([double(x3), double(x5)])

    0.1000   -0.1000

Para el segundo modo de frecuencia ω₂=3.3166, los osciladores están en oposición de fase, las amplitudes son las mismas

Sistema de N partículas unidas a N+1 muelles elásticos

Consideremos un sistema formado por N partículas de masa m unidas a N+1 muelles elásticos de constante k. En la figura mostramos 10 partículas unidas a 11 muelles elásticos. Señalamos los 2N+2=22 puntos cuyo estado tenemos que determinar

$\begin{array}{l} (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) = T_{s} (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2} \\ F_{2} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) = (T_{p} T_{s}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{4} \\ F_{4} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{3} \\ F_{3} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) = T_{s} (T_{p} T_{s}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{5} \\ F_{5} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{4} \\ F_{4} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) = {(T_{p} T_{s})}^{2} (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ ... \\ (\begin{matrix} x_{2 N + 1} \\ F_{2 N + 1} \end{matrix}) = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) (\begin{matrix} x_{2 N} \\ F_{2 N} \end{matrix}) = {(T_{p} T_{s})}^{N} (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{2 N + 2} \\ F_{2 N + 2} \end{matrix}) = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) (\begin{matrix} x_{2 N + 1} \\ F_{2 N + 1} \end{matrix}) = T_{s} {(T_{p} T_{s})}^{N} (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \\ (\begin{matrix} x_{2 N + 2} \\ F_{2 N + 2} \end{matrix}) = (\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}) (\begin{matrix} x_{1} \\ F_{1} \end{matrix}) \end{array}$

Condiciones de contorno

Las condiciones de contorno son:

x₁=0, ya que el punto 1 es fijo
x_2N+2=0, ya que el extremo 2N+2 es fijo

$(\begin{matrix} 0 \\ F_{2 N + 2} \end{matrix}) = (\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}) (\begin{matrix} 0 \\ F_{1} \end{matrix})$

Lo que implica que el elemento de la matriz T₁₂=0

En la página titulada Modos normales de vibración (I) calculamos las frecuencias de los modos normales de vibración del sistema formado por N=2, 3 y 4, partículas de masas m unidas a muelles elásticos de constante k. Probamos con N=4

Frecuencias de los modos normales de oscilación

Utilizamos Math Symbolic de Matlab para realizar la multiplicación de matrices

syms k m w;
N=4; %número de partículas
Ts=[1,1/k;0,1];
Tp=[1,0;-m*w^2,1];
T=Ts*(Tp*Ts)^N;

Comprobamos que el determinante de la matriz T es la unidad

>> det(T)
ans =1

Utilizamos la función solve para calcular las raíces positivas de la ecuación T₁₂=0.

>> solve(T(1,2))
ans =
 -(-(k*(5^(1/2) - 3))/(2*m))^(1/2)
  -((k*(5^(1/2) + 3))/(2*m))^(1/2)
 -(-(k*(5^(1/2) - 5))/(2*m))^(1/2)
  -((k*(5^(1/2) + 5))/(2*m))^(1/2)
  (-(k*(5^(1/2) - 3))/(2*m))^(1/2)
   ((k*(5^(1/2) + 3))/(2*m))^(1/2)
  (-(k*(5^(1/2) - 5))/(2*m))^(1/2)
   ((k*(5^(1/2) + 5))/(2*m))^(1/2)

$ω_{1} = \sqrt{\frac{k}{m} \frac{3 - \sqrt{5}}{2}} ω_{2} = \sqrt{\frac{k}{m} \frac{5 - \sqrt{5}}{2}} ω_{3} = \sqrt{\frac{k}{m} \frac{3 + \sqrt{5}}{2}} ω_{4} = \sqrt{\frac{k}{m} \frac{5 + \sqrt{5}}{2}}$

Amplitudes del MAS que describe de cada una de las partículas

La amplitud de la primera partícula es q₁=x₂=x₃
La amplitud de la segunda partícula es q₂=x₄=x₅
La amplitud de la tercera partícula es q₃=x₆=x₇
La amplitud de la cuarta partícula es q₄=x₈=x₉

$\begin{array}{l} q_{1} = (\begin{matrix} 1 & 0 \end{matrix}) (T_{p} T_{s}) (\begin{matrix} 0 \\ 1 \end{matrix}) \\ q_{2} = (\begin{matrix} 1 & 0 \end{matrix}) {(T_{p} T_{s})}^{2} (\begin{matrix} 0 \\ 1 \end{matrix}) \\ q_{3} = (\begin{matrix} 1 & 0 \end{matrix}) {(T_{p} T_{s})}^{3} (\begin{matrix} 0 \\ 1 \end{matrix}) \\ q_{4} = (\begin{matrix} 1 & 0 \end{matrix}) {(T_{p} T_{s})}^{4} (\begin{matrix} 0 \\ 1 \end{matrix}) \end{array}$

Una vez que se han calculado las amplitudes q_j con j=1,2,...N, de cada una de las partículas se normalizan de acuerdo a la siguiente fórmula

$\sum_{j = 1}^{N} m_{j} q_{j}^{2} = 1$

donde m_j es la masa de cada partícula

Completamos el script anterior para calcular y representar las amplitudes de la oscilación de cada una de las partículas para la frecuencia del modo seleccionado

....
masa=1; %masa
cte=1; %constante del muelle
w1=sqrt((3-sqrt(5))/2); %frecuencia del primer modo normal
Vs=subs(Ts,k,cte);
Vp=subs(Tp,{m,w},{masa,w1});
q=zeros(N,1);
suma=0;
for j=1:N
    q(j)=[1,0]*(Vp*Vs)^j*[0;1];
    suma=suma+masa*q(j)^2;
end
for j=1:N
    q(j)=q(j)/sqrt(suma); %amplitudes
end
stem(q)
xlim([0,N+1])
xlabel('j')
ylabel('q_j')
title('Amplitudes de la oscilación')

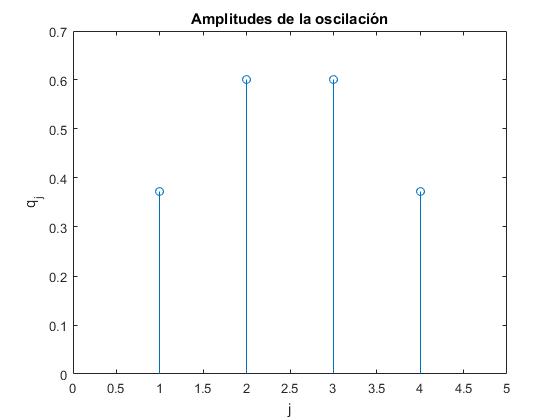
Calculamos las amplitudes q_j(ω_r) con j=1,2,...N para la frecuencia ω_r de un modo normal de vibración y las amplitudes q_j(ω_s) para la frecuencia ω_s de otro modo normal de vibración r≠s. Comprobamos que se cumple que

$\sum_{j = 1}^{N} m_{j} q_{j} (ω_{r}) \cdot q_{j} (ω_{s}) = 0$

Hemos calculado las amplitudes q_j para la frecuencia del modo fundamental ω₁. Duplicamos el código para calcular las amplitudes y_j para el tercer modo de vibración ω₃

syms k m w;
N=4; %número de partículas
Ts=[1,1/k;0,1];
Tp=[1,0;-m*w^2,1];
T=Ts*(Tp*Ts)^N;

masa=1; %masa
cte=1; %constante del muelle
w1=sqrt((3-sqrt(5))/2); %frecuencia del primer modo 
Vs=subs(Ts,k,cte);
Vp=subs(Tp,{m,w},{masa,w1});
q=zeros(N,1);
suma=0;
for j=1:N
    q(j)=[1,0]*(Vp*Vs)^j*[0;1];
    suma=suma+masa*q(j)^2;
end
for j=1:N
    q(j)=q(j)/sqrt(suma);
end

w3=sqrt((3+sqrt(5))/2); %frecuencia del tercer modo 
Vs=subs(Ts,k,cte);
Vp=subs(Tp,{m,w},{masa,w3});
y=zeros(N,1);
suma=0;
for j=1:N
    y(j)=[1,0]*(Vp*Vs)^j*[0;1];
    suma=suma+masa*y(j)^2;
end
for j=1:N
    y(j)=y(j)/sqrt(suma);
end

suma=0;
for j=1:N
    suma=suma+masa*q(j)*y(j);
end
disp(suma)

   1.1102e-16

Sistema homogéneo

En esta página, hemos estudiado un sistema formado por partículas unidas a muelles elásticos. Calculamos mediante el procedimiento descrito en esta página:

Las frecuencias de los modos normales de vibración
Las amplitudes del MAS que describe cada una de las partículas para la frecuencia del modo seleccionado

El sistema más importante consta de N partículas de la misma masa m unidas a N+1 muelles de la misma constante k

La matriz T que relaciona los estados de los puntos extremos 1 y 2N+2 es

$\begin{array}{l} T = T_{s} {(T_{p} T_{s})}^{N} \\ T_{s} = (\begin{matrix} 1 & 1 / k \\ 0 & 1 \end{matrix}) T_{p} = (\begin{matrix} 1 & 0 \\ - m ω^{2} & 1 \end{matrix}) \end{array}$

Se utiliza la función solve de MATLAB para calcular las raíces reales y positivas de la ecuación T₁₂=0.

Para la frecuencia ω del modo normal de vibración seleccionado, se calculan las amplitudes q_j del MAS que describe cada una de las partículas del sistema. Se normalizan y se representan gráficamente

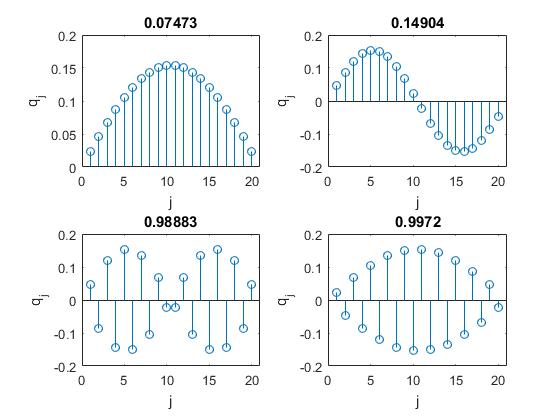
$q_{j} = (\begin{matrix} 1 & 0 \end{matrix}) {(T_{p} T_{s})}^{j} (\begin{matrix} 0 \\ 1 \end{matrix})$

En el siguiente script representamos las amplitudes q_j de los dos primeros modos de vibración y de los dos últimos modos para un sistema de N=20 partículas, de masa m=4 unidas a muelles de constante k=1. En el título de cada uno de los gráficos aparece la frecuencia

syms k m w;
N=20; %número de partículas
masa=4; %masa
cte=1; %constante del muelle
Ts=[1,1/k;0,1];
Tp=[1,0;-m*w^2,1];
T=Ts*(Tp*Ts)^N;
V=subs(T,{k,m},{cte,masa});
W=double(solve(V(1,2))); %complejas
Wr=zeros(N,1); %reales
j=1;
for i=1:length(W)
    if real(W(i))>0
        Wr(j)=real(W(i));
        j=j+1;
    end
end
Wr=sort(Wr); %frecuencias
disp(Wr)

%amplitudes
q=zeros(N,1);
ventana=1;
Vs=subs(Ts,k,cte);
for s=[1,2,19,20] % modos seleccionados
    w1=Wr(s); %frecuencia del primer modo de vibración
    Vp=subs(Tp,{m,w},{masa,w1});
    suma=0;
    for j=1:N
        q(j)=[1,0]*(Vp*Vs)^j*[0;1];
        suma=suma+masa*q(j)^2;
    end
    for j=1:N
        q(j)=q(j)/sqrt(suma);
    end
    subplot(2,2,ventana)
    stem(q);
    xlim([0,N+1])
    xlabel('j')
    ylabel('q_j')
    title(num2str(w1))
    ventana=ventana+1;
end

Frecuencias de los N=20 modos normales de vibración ordenadas de menor a mayor