Oscilaciones forzadas en un sistema formado por partículas unidas por muelles (IV)
Fuerza no periódica
Sin rozamiento
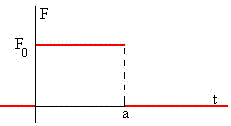
En la figura, se muestra la fuerza que actúa sobre la segunda partícula
En las páginas anteriores, calculamos los valores propios y los vectores propios de la matriz M-1·K, donde M es la matriz diagonal de las masas y K de las constantes elásticas de los muelles.
>> [V,D]=eig(inv(M)*K)
La matriz diagonal D contiene en su diagonal principal los cuadrados de las frecuencias de los modos normales de vibración, ω1 y ω2.
Los vectores columna de la matriz V son los vectores propios correspondientes a cada uno de los valores propios. Modificamos la matriz V multiplicando cada vector propio por un factor de escala, de modo que se cumpla
>> M=sym('[2,0;0,1]');
>> K=sym('[9,-3;-3,3]');
>> [V,D]=eig(inv(M)*K)
V =
[ 1/2, -1]
[ 1, 1]
D =
[ 3/2, 0]
[ 0, 6]
Los cuadrados de las frecuencias de los modos normales de vibración son los elementos de la diagonal de la matriz D.
La nueva matriz V es
Definimos el vector u(t) de modo que
En el espacio u, el comportamiento del sistema se describe mediante un sistema de dos ecuaciones diferenciales desacopladas
donde
En la página web "Respuesta de un oscilador a una fuerza no periódica" estudiamos la función escalón. Para el caso en que no exista fuerza de rozamiento, γ=0, por lo que ω=ω0.
Las soluciones de las ecuaciones diferenciales desacopladas son, respectivamente:
Calculamos las posiciones x1(t) y x2(t) de cada una de las partículas mediante la transformación x=V·u
Elaboramos un script para representar las posiciones x1(t) y x2(t) de cada una de las partículas para una anchura del pulso rectangular coincidente con el periodo del segundo modo normal de vibración a=2π/ω2 y para un valor F0=2 de la fuerza.
syms t a;
M=sym('[2,0;0,1]');
K=sym('[9,-3;-3,3]');
[V,D]=eig(inv(M)*K);
w=diag(sqrt(D)); %vector de frecuencias propias
n=length(w);
%calcula una nueva matriz V
for i=1:n
r=V(:,i)'*M*V(:,i);
V(:,i)=V(:,i)/sqrt(r);
end
%vector fuerza
F0=sym('[0;2]');
f0=V'*F0;
u=diag(f0'*inv(M*D))*((1-cos(w*t))-(1-cos(w*(t-a)))*heaviside(t-a));
x=V*u;
x=subs(x,a,2*pi/w(2));
%representación gráfica
color=['b','r','g'];
hold on
for i=1:n
h=ezplot(x(i),[0,15]);
set(h,'color',color(i))
end
title('Dos osciladores acoplados, forzados')
ylabel('x1,x2')
xlabel('t')
grid on
hold off
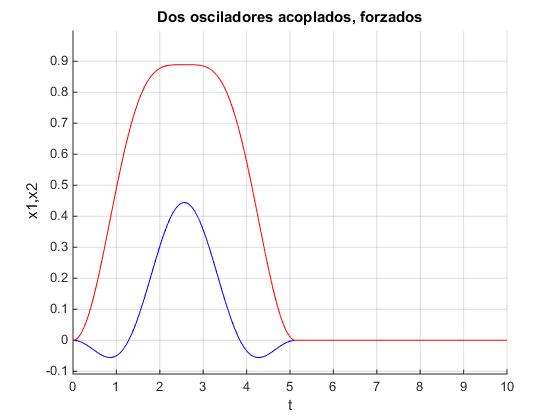
Cuando la anchura del pulso rectangular coincide con el periodo del primer modo normal de vibración a =2π/ω1, la oscilación se detiene completamente tal como se observa en la figura.
Con rozamiento
Como hemos descrito en la página anterior, la matriz C de los coeficientes de la fuerza de rozamiento, no es habitualmente diagonalizable, pero hay procedimientos que nos permiten diagonalizarla y hacer que las ecuaciones que describen el movimiento oscilatorio de cada partícula del sistema en el espacio u se desacoplen.
Para cada una de las partículas 2γ adquiere el valor de los elementos de la matriz diagonal Cg. Las frecuencias propias ω0 son las frecuencias de los modos normales de vibración, cuyos cuadrados están en la diagonal de la matriz D de los valores propios y f(t) es la fuerza transformada que actúa sobre cada partícula.
En el caso de un pulso rectangular de altura F0 y anchura a, la repuesta del oscilador amortiguado ya se ha estudiado en la página titulada "Respuesta de un oscilador a una fuerza no periódica"
Calculamos las posiciones x1(t) y x2(t) de cada una de las partículas mediante la transformación x=V·u
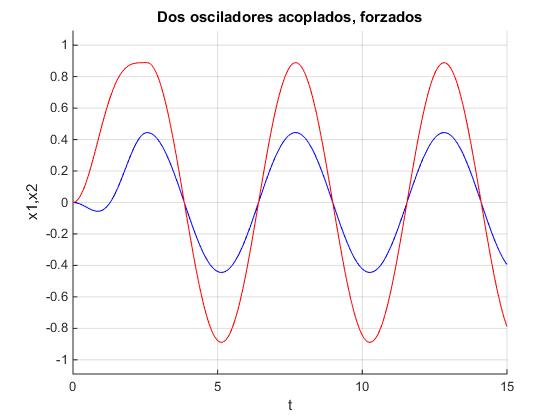
Elaboramos un script para representar las posiciones x1(t) y x2(t) de cada una de las partículas para una anchura del pulso rectangular coincidente con el periodo del segundo modo normal de vibración a=2π/ω2 y para un valor F0=2 de la fuerza. La amplitud de la oscilación decrece con el tiempo.
syms t wf c a;
M=sym('[2,0;0,1]');
K=sym('[9,-3;-3,3]');
C=sym('[2*c,-c;-c,c]');
C=subs(C,c,sym('1/2')); %cambiar el rozamiento c
[V,D]=eig(inv(M)*K);
w0=diag(sqrt(D)); %vector de frecuencias propias
n=length(w0);
%calcula una nueva matriz V
for i=1:n
r=V(:,i)'*M*V(:,i);
V(:,i)=V(:,i)/sqrt(r);
end
%la matriz C se hace diagonal
for i=1:n
Cg(i,i)= V(:,i)'*C*V(:,i)/(V(:,i)'*V(:,i));
end
g=diag(Cg)/2;
%vector fuerza
F0=sym('[0;2]');
f0=V'*F0;
w=sqrt(w0.^2-g.^2); %frecuencia de la oscilación amortiguada
u=diag(f0'*inv(M*D))*((1-exp(-g*t).*(cos(w*t)+(g./w).*sin(w*t)))
-(1-exp(-g*(t-a)).*(cos(w*(t-a))+(g./w).*sin(w*(t-a))))*heaviside(t-a));
x=V*u;
x=subs(x,a,2*pi/w(2)); %cambiar la anchura del pulso
%representación gráfica
color=['b','r','g'];
hold on
for i=1:n
h=ezplot(x(i),[0,20]);
set(h,'color',color(i))
end
title('Dos osciladores acoplados, forzados')
ylabel('x1,x2')
xlabel('t')
grid on
hold off
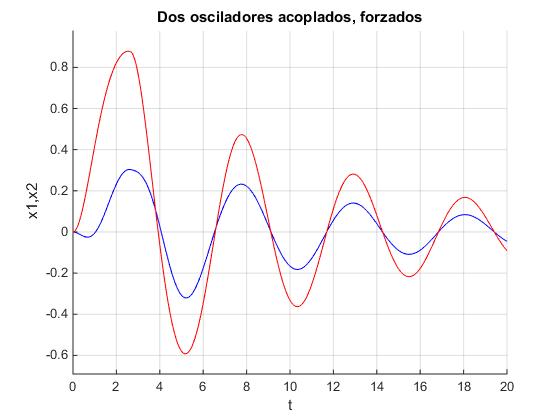
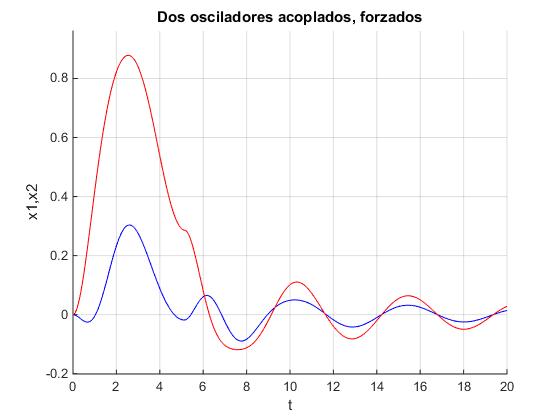
Cuando la anchura del pulso rectangular coincide con el periodo del primer modo normal de vibración a=2π/ω1 la oscilación ya no se detiene como se observa en la figura. La amplitud de la oscilación decrece con el tiempo.