Modos normales de vibración (II)
Sistema formado por partículas de la misma masa unidas por muelles elásticos de distinta constante

Vamos a estudiar sistemas formados por dos y tres partículas de la misma masa unidas por muelles de constantes k (azul) y g (rojo). Se generalizará sin dificulad a un sistema formado por N partículas.
Sistema formado por dos partículas
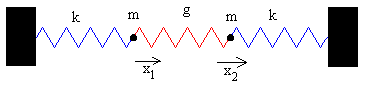
Ecuaciones del movimiento
En forma matricial
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz M-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k g m;
>> M=[m,0;0,m];
>> K=[k+g,-g;-g,k+g];
>> [V,D]=eig(M^-1*K);
>> w2 =diag(D)
w2=
k/m
(2*g + k)/m
>> V
V =
[ 1, -1]
[ 1, 1]
| Valores propios ω2 | Vectores propios |
| (1,1) | |
| (-1,1) |
Sea un sistema formado por dos partículas de masa m=1, unidas por muelles de constantes k=1 y g=2. las frecuencias de los modos normales de vibración son. ω1=1 y ω2=
Sistema formado por tres partículas
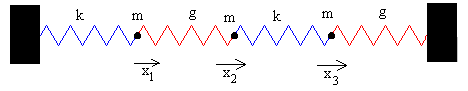
Ecuaciones del movimiento
En forma matricial, el sistema de ecuaciones se expresa
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz M-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k g m;
>> M=[m,0;0,m];
>> K=[k+g,-g;-g,k+g];
>> [V,D]=eig(M^-1*K);
>> w2 =diag(D)
>> w2 =
(g + k - (g^2 + k^2)^(1/2))/m
(g + k)/m
(g + k + (g^2 + k^2)^(1/2))/m
>> simplify(V)
ans =
[ g/k, -k/g, g/k]
[ (g^2 + k^2)^(1/2)/k, 0, -(g^2 + k^2)^(1/2)/k]
[ 1, 1, 1]
| Valores propios ω2 | Vectores propios |
Sea un sistema formado por dos partículas de masa m=1, unidas por por muelles de constantes k=1 y g=2. Las frecuencias de los modos normales de vibración son. ω1=, ω2= y ω3=
Sistema formado por N partículas
La matriz de la masa M es diagonal cuyos elementos son la masa m de las partículas. La matriz K es
Actividades
Se ha fijado
- La masa de las partículas, m=1 kg
- La constante elástica de los muelles de color azul, k=1N/m
Se introduce
- El número N de partículas, en el control titulado Número de partículas
-
La constante elástica de los muelles de color rojo, g, en el control titulado Constante
Se pulsa el botón titulado Nuevo
Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular ω1.
Se pulsa el botón titulado >>, observamos los siguientes modos normales ω2, … etc.
Se pulsa el botón titulado << para observar el modo normal de vibración anterior.
Las frecuencias de los modos de vibración se guardan en el control área de texto situado a la izquierda del applet.
Oscilaciones de una cadena diatómica lineal

Vamos a estudiar sistemas formados por dos y tres partículas de masas M y m alternadas unidas por muelles de la misma constante k. Se generalizará sin dificulad a un sistema formado por N partículas.
Sistema formado por dos partículas N=2
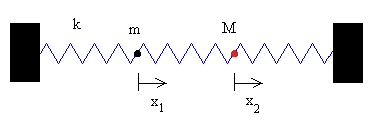
Ecuaciones del movimiento
En forma matricial, el sistema de ecuaciones se expresa
La primera es la matriz que ahora denominaremos Masa (para evitar confundirla con la masa M de las partículas) de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz Masa-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k M m; >> Masa=[m,0;0,M]; >> K=[2*k,-k;-k,2*k]; >> [V,D]=eig(Masa^-1*K); >> w2 =diag(D) >> w2 = (M*k + k*(M^2 - M*m + m^2)^(1/2) + k*m)/(M*m) (M*k - k*(M^2 - M*m + m^2)^(1/2) + k*m)/(M*m)Ejemplo
Sea el sistema formado por dos partículas de masas m=1 y M=2, unidas por muelles de constantes k=1
>> w2=subs(w2,{m,M,k},{1,2,1});
>> sqrt(w2)
ans =
(3^(1/2)/2 + 3/2)^(1/2)
(3/2 - 3^(1/2)/2)^(1/2)
>> double(ans)
ans =
1.5382
0.7962
Sistema formado por tres partículas N=3

Ecuaciones del movimiento
En forma matricial, el sistema de ecuaciones se expresa
La primera es la matriz Masa de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz Masa-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k M m;
>> Masa=[m,0,0;0,M,0;0,0,m];
>> K=[2*k,-k,0;-k,2*k,-k;0,-k,2*k];
>> [V,D]=eig(Masa^-1*K);
>> w2=diag(D)
w2 =
(k*(M^2 + m^2)^(1/2) + M*k + k*m)/(M*m)
(M*k - k*(M^2 + m^2)^(1/2) + k*m)/(M*m)
(2*k)/m
Ejemplo
Sea el sistema formado por dos partículas de masas m=1 y M=2, unidas por muelles de constantes k=1
>> w2=subs(w2,{m,M,k},{2,1,1})
>> sqrt(w2)
ans =
(5^(1/2)/2 + 3/2)^(1/2)
(3/2 - 5^(1/2)/2)^(1/2)
2^(1/2)
>> double(ans)
ans =
ans =
1.6180
0.6180
1.4142
Una particularidad importante es que la matriz Masa-1K ha dejado de ser simétrica
>> (Masa^-1*K) ans = [ (2*k)/m, -k/m, 0] [ -k/M, (2*k)/M, -k/M] [ 0, -k/m, (2*k)/m]
Lo que es importante a la hora de elegir procedimientos para calcular los valores y vectores propios. Por ejemplo, el procedimiento de Jacobi solamente es aplicable a matrices simétricas
Sistema formado por N partículas
Para N partículas calculamos los valores y los vectores propios de la matriz Masa-1K
Como la matriz no es simétrica no podemos aplicar en la simulación (más abajo) el procedimiento de Jacobi. Como alternativa, obtenemos los coeficientes del polinomio característico aplicando el procedimiento de Leverrier y calculamos las raíces del polinomio aplicando el procedimiento del punto medio para raíces múltiples.
Actividades
Se ha fijado
- La masa, m=1 kg
- La constante elástica de los muelles, k=1 N/m
Se introduce
- El número N de partículas, en el control titulado Número de partículas
- La masa M de las otras partículas en el control titulado Masa
Se pulsa el botón titulado Nuevo
Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular ω1.
Se pulsa el botón titulado >>, observamos los siguientes modos normales ω2, … etc.
Se pulsa el botón titulado << para observar el modo normal de vibración anterior.

