Oscilaciones forzadas en un sistema formado por partículas unidas por muelles (I)
Una partícula unida a un muelle elástico
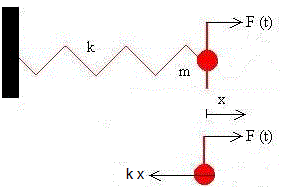
Escribimos la ecuación del movimiento aplicando la segunda ley de Newton y a continuación, otra ecuación equivalente en la que se ha sustituido k/m por el cuadrado de ω0 que es la frecuencia propia o natural del oscilador. Esta segunda forma es más general que la primera y es válida para cualquier tipo de oscilador
En el estado estacionario, la solución de esta ecuación diferencial es de la forma x(t)=Acos(ωt)+Bsin(ωt). Calculamos los coeficientes A y B, introduciendo la solución en la ecuación diferencial
Que dan lugar al siguiente sistema de dos ecuaciones con dos incógnitas
El resultado es el siguiente: B=0,
Representamos la amplitud A en función de x=ω/ω0
fplot('1/(1-x^2)',[0,3])
ylim([-5,5])
grid on
xlabel('\omega/\omega_0')
ylabel('A')
title('Un oscilador')
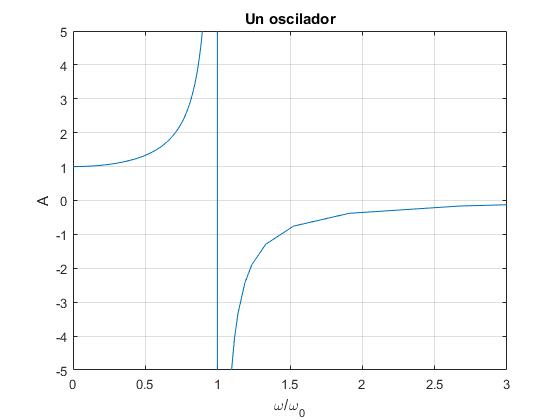
Las amplitudes A se hace infinita, cuando el denominador se hace cero, ω/ω0=1
- Para ω<ω0, A>0, el movimiento de la partícula está en fase con la fuerza oscilante. x(t)=Acos(ωt)
- Para ω>ω0, A<0, el movimiento de la partícula está en oposición de fase con la fuerza oscilante. x(t)=|A|cos(ωt+π)
Dos osciladores acoplados
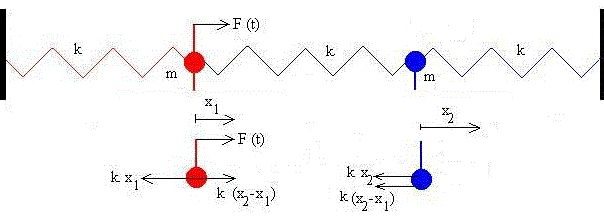
Escribimos la ecuación del movimiento aplicando la segunda ley de Newton y a continuación, otra ecuación equivalente en la que se ha sustituido k/m por el cuadrado de ω0 que es la frecuencia propia o natural del oscilador.
En el estado estacionario, la solución de este sistema de dos ecuaciones diferenciales tiene la forma x1(t)=A1cos(ωt)+B1sin(ωt) y x2(t)=A2cos(ωt)+B2sin(ωt). Calculamos los coeficientes A1, B1, A2 y B2, introduciendo las soluciones x1(t) y x2(t) en el segundo sistema de ecuaciones diferenciales.
Que dan lugar al siguiente sistema de cuatro ecuaciones con cuatro incógnitas
syms w w0 F0 m; A=[(2*w0^2-w^2),-w0^2,0,0; -w0^2,(2*w0^2-w^2),0,0; 0,0 (2*w0^2-w^2), -w0^2;0,0,-w0^2,(2*w0^2-w^2)]; b=[F0/m;0;0;0]; X=A\b
X =
-(F0*(w^2 - 2*w0^2))/(m*(w^4 - 4*w^2*w0^2 + 3*w0^4))
(F0*w0^2)/(m*(w^4 - 4*w^2*w0^2 + 3*w0^4))
0
0
El resultado es el siguiente: B1=0, B2=0
Representamos las amplitudes A1 y A2 en función de x=ω/ω0
A1=@(x) (2-x^2)/(x^4-4*x^2+3);
A2=@(x) 1/(x^4-4*x^2+3);
hold on
fplot(A1,[0,3]);
fplot(A2,[0,3]);
hold off
ylim([-5,5])
grid on
legend('A_1', 'A_2')
xlabel('\omega/\omega_0')
ylabel('A_1, A_2')
title('Dos osciladores')
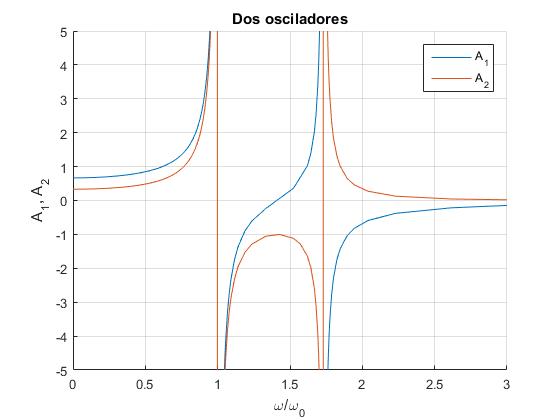
Las amplitudes A1 y A2 se hacen infinitas, cuando el denominador se hace cero
>> solve(x^4-4*x^2+3)
ans =
-1
1
3^(1/2)
-3^(1/2)
Las raíces positivas son ω/ω0=1, ω/ω0=
La amplitud A1 se hace cero para ω/ω0=
En la figura, apreciamos los intervalos de frecuencias en los que A1>0 es decir, el movimiento de la primera partícula está en fase con la fuerza oscilante, x1(t)=A1cos(ωt) y los intervalos de frecuencias en los que A1<0 es decir, el movimiento de la primera partícula está en oposición fase con la fuerza oscilante, x1(t)=|A1|cos(ωt+π). Lo mismo podríamos decir para A2
Tres osciladores acoplados
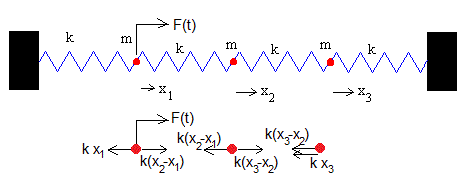
Escribimos la ecuación del movimiento aplicando la segunda ley de Newton y a continuación, otra ecuación equivalente en la que se ha sustituido k/m por el cuadrado de ω0 que es la frecuencia propia o natural del oscilador.
En el estado estacionario, la solución de este sistema de tres ecuaciones diferenciales tiene la forma x1(t)=A1cos(ωt)+B1sin(ωt), x2(t)=A2cos(ωt)+B2sin(ωt) y x3(t)=A3cos(ωt)+B3sin(ωt). Calculamos los coeficientes A1, B1, A2, B2, A3, B3 introduciendo las soluciones x1(t), x2(t) y x3(t) en el segundo sistema de ecuaciones diferenciales.
Dando lugar al siguiente sistema de seis ecuaciones con seis incógnitas
syms w w0 F0 m; A=[(2*w0^2-w^2),-w0^2,0,0,0,0;-w0^2,(2*w0^2-w^2),-w0^2,0,0,0;0, -w0^2,(2*w0^2-w^2),0,0,0;0,0,0,(2*w0^2-w^2),-w0^2,0;0,0,0,-w0^2,(2*w0^2-w^2), -w0^2;0,0,0,0,-w0^2,(2*w0^2-w^2)]; b=[F0/m;0;0;0;0;0]; X=A\b
X =
-(F0*(w^4 - 4*w^2*w0^2 + 3*w0^4))/(m*(w^2 - 2*w0^2)*(w^4 - 4*w^2*w0^2 + 2*w0^4))
(F0*w0^2)/(m*(w^4 - 4*w^2*w0^2 + 2*w0^4))
-(F0*w0^4)/(m*(w^6 - 6*w^4*w0^2 + 10*w^2*w0^4 - 4*w0^6))
El resultado es el siguiente: B1=0, B2=0 y B3=0
Representamos las amplitudes A1, A2 y A3 en función de x=ω/ω0
A1=@(x) (3-4*x^2+x^4)/(4-10*x^2+6*x^4-x^6);
A2=@(x) 1/(x^4-4*x^2+2);
A3=@(x) 1/(4-10*x^2+6*x^4-x^6);
hold on
fplot(A1,[0,3]);
fplot(A2,[0,3]);
fplot(A3,[0,3]);
hold off
ylim([-5,5])
grid on
legend('A_1', 'A_2', 'A_3')
xlabel('\omega/\omega_0')
ylabel('A_1, A_2, A_3')
title('Tres Osciladores')
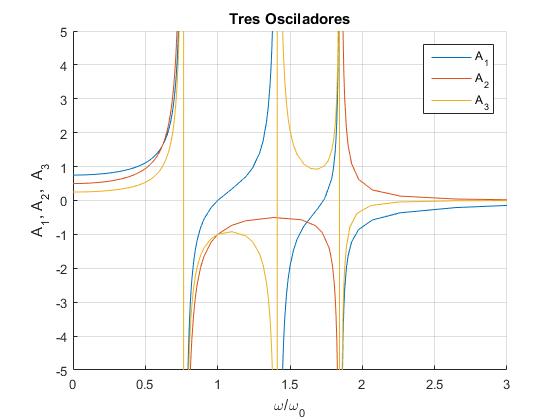
Las amplitudes A1, A3 y A2 se hacen infinitas, cuando el denominador se hace cero
>> solve(4-10*x^2+6*x^4-x^6)
ans =
(2^(1/2) + 2)^(1/2)
2^(1/2)
-(2^(1/2) + 2)^(1/2)
(2 - 2^(1/2))^(1/2)
-2^(1/2)
-(2 - 2^(1/2))^(1/2)
>> solve(x^4-4*x^2+2)
ans =
(2^(1/2) + 2)^(1/2)
-(2^(1/2) + 2)^(1/2)
(2 - 2^(1/2))^(1/2)
-(2 - 2^(1/2))^(1/2)
Las raíces positivas son ω/ω0=, ω/ω0= , ω/ω0=
La amplitud A1 se hace cero para ω/ω0=1 y para ω/ω0=
>> solve(3-4*x^2+x^4)
ans =
-1
1
3^(1/2)
-3^(1/2)
n osciladores acoplados
Se puede encontrar una solución analítica para n osciladores, véase el artículo citado en las referencias.
Referencias
Somayyeh Belbasi, M. Ebrahim Foulaadvand, Yong S. Joe. Anti-resonance in a one-dimensional chain of driven coupled oscillators Am. J. Phys. 82, 32, (2014), doi: 10.1119/1.4827277

