Oscilaciones forzadas en un sistema formado por partículas unidas por muelles (II)
Sin rozamiento
La solución de estas ecuaciones diferenciales es la suma de la solución de la ecuación homogénea que depende de las condiciones iniciales y la solución particular. El primer término describe el estado transitorio que desaparece al cabo de cierto tiempo (teóricamente infinito) si hay rozamiento y el segundo, el estado estacionario.
Primero, consideraremos que no hay rozamiento que es el caso más sencillo y posteriormente, le añadiremos el rozamiento en las páginas siguientes.
En este apartado, estudiaremos el comprortamiento de un sistema bajo la acción de fuerzas, sin tener en cuenta el rozamiento.
En la figura, representamos un sistema de dos partículas de masas m1 y m2 unidas por tres muelles de constantes k1, k2 y k3. Sobre la primera partícula actúa una fuerza dependiente del tiempo F1(t) y sobre la segunda la fuerza F2(t). Las ecuaciones del movimiento son
En forma matricial escribimos
En la página anterior, calculamos los valores propios y los vectores propios de la matriz M-1·K, donde M es la matriz diagonal de las masas y K de las constantes elásticas de los muelles.
>> [V,D]=eig(inv(M)*K)
La matriz diagonal D contiene en su diagonal principal los cuadrados de las frecuencias de los modos normales de vibración, ω1 y ω2.
Los vectores columna de la matriz V son los vectores propios correspondientes a cada uno de los valores propios. Modificamos la matriz V multiplicando cada vector propio por un factor de escala, de modo que se cumpla
Definimos un nuevo vector u(t) de modo que
La ecuación diferencial del movimiento en forma matricial se transforma en
El comportamiento del sistema se describe mediante un sistema de dos ecuaciones diferenciales desacopladas
La solución de cada una de estas ecuaciones diferenciales es la suma de su homogénea que depende de las condiciones iniciales y de la solución particular que depende de la expresión de cada una de las fuerzas f1(t) y f2(t).
Una vez que obtenemos las soluciones en términos de las coordendas u1(t) y u2(t) se vuelven a transformar en coordenadas físicas x1(t) y x2(t), mediante x=V·u.
Ejemplo 1
En la figura al principio de la página, sea el sistema de dos partículas de masas m1=2 y m2=1, unidas por muelles de constantes k1=6, k2=3 y k3=0. Sobre la segunda partícula, actúa una fuerza F2(t)=2·cos(ωf t), sobre la primera no actúa ninguna fuerza F1(t)=0.
Las ecuaciones del movimiento en forma matricial se escriben
Calculamos los valores propios (cuadrados de las frecuencias de los modos normales de vibración) y los vectores propios correspondientes a cada valor propio de la matriz M-1·K
>> M=sym('[2,0;0,1]');
>> K=sym('[9,-3;-3,3]');
>> [V,D]=eig(inv(M)*K)
V =
[ 1/2, -1]
[ 1, 1]
D =
[ 3/2, 0]
[ 0, 6]
Los cuadrados de las frecuencias de los modos normales de vibración son los elementos de la diagonal de la matriz D.
Creamos una nueva matriz V, multiplicando los vectores propios por un factor de escala de modo que
>> X1=V(:,1); >> X2=V(:,2); >> r=X1'*M*X1 r =3/2 >> X1=X1/sqrt(r); >> r=X2'*M*X2 r =3 >> X2=X2/sqrt(r); >> V=[X1,X2] V = [ 6^(1/2)/6, -3^(1/2)/3] [ 6^(1/2)/3, 3^(1/2)/3] >> Mg=V'*M*V Mg = [ 1, 0] [ 0, 1] >> Kg=V'*K*V Kg = [ 3/2, 0] [ 0, 6]
La nueva matriz V es
En el sistema de coordenadas u, que hemos definido mediante la transformación x=V·u, las fuerzas f1(t) y f2(t) se expresan
>> syms t wf;
>> F=[0;2*cos(wf*t)];
>> f=V'*F
f =
(2*2^(1/2)*3^(1/2)*cos(t*wf))/3
(2*3^(1/2)*cos(t*wf))/3
Las ecuaciones diferenciales del movimiento se desacoplan y su solución particular se puede calcular fácilmente
Solución de la primera ecuación diferencial
Solución de la segunda ecuación diferencial
La solución particular es up=Acos(ωf·t). Introducimos la solución particular en la ecuación diferencial para calcular el coeficiente A
La solución completa es la suma de la homogénea más la particular
Los coeficientes C y D se calculan a partir de las condiciones iniciales. Conocido x1(0) y x2(0), obtenemos las condiciones iniciales u1(0) y u2(0) mediante la transformación u0=V-1·x0. Se procede del mismo modo para las velocidades iniciales.
En este ejercicio, x1(0)=0 y x2(0)=0 por lo que u1(0)=0 y u2(0)=0. Lo mismo para las velocidades
La solución de la primera ecuación diferencial es
Análogamente a la de la primera ecuación diferencial
Calculamos las posiciones x1(t) y x2(t) de cada una de las partículas mediante la transformación x=V·u
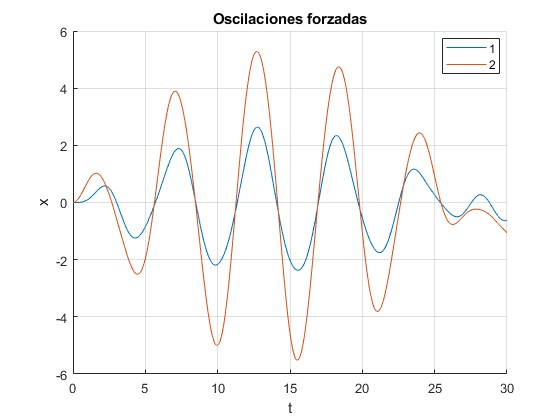
Representamos x1(t) y x2(t) para ωf=1.
w1=sqrt(3/2); %frecuencias de los modos normales
w2=sqrt(6);
w=1; %fuerza oscilante
x1=@(t) 2*(cos(w*t)-cos(w1*t))/(3*(w1^2-w^2))-2*(cos(w*t)-cos(w2*t))
/(3*(w2^2-w^2));
x2=@(t) 4*(cos(w*t)-cos(w1*t))/(3*(w1^2-w^2))+2*(cos(w*t)-cos(w2*t))
/(3*(w2^2-w^2));
hold on
fplot(x1,[0,30])
fplot(x2,[0,30])
hold off
grid on
xlabel('t')
ylabel('x')
legend('1','2','Location', 'best')
title('Oscilaciones forzadas')
Ejemplo 2
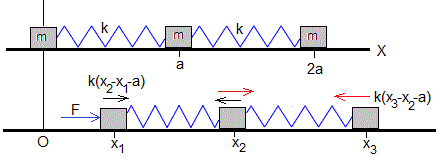
Tres cuerpos de masa m están conectados por muelles de constante k. El movimiento se produce a lo largo del eje X.
En el instante inicial, los cuerpos están en reposo en las posiciones 0, a y 2a, siendo a la longitud del muelle sin deformar.
Se aplica una fuerza oscilante fcos(ωt) al primer cuerpo. Vamos a determinar el movimiento de cada uno de los cuerpos.
En la figura, se muestran las fuerzas sobre los cuerpos, suponiendo que x2-x1>a y que x3-x2>a. La fuerza que ejerce un muelle sobre un cuerpo es igual y de sentido contrario a la que ejerce dicho muelle sobre el otro cuerpo
Las ecuaciones del movimiento son
En forma matricial
>> syms m k positive; >> M=[m,0,0;0,m,0;0,0,m] M = [m, 0, 0] [0, m, 0] [0, 0, m] >> K=[k,-k,0;-k,2*k,-k;0,-k,k] K = [ k, -k, 0] [-k, 2*k, -k] [ 0, -k, k] >> [V,D]=eig(inv(M)*K) V = [1, -1, 1] [1, 0, -2] [1, 1, 1] D = [0, 0, 0] [0, k/m, 0] [0, 0, (3*k)/m]
Las frecuencias propias son
Creamos una nueva matriz V, multiplicando los vectores propios por un factor de escala
>> X1=V(:,1); >> X2=V(:,2); >> X3=V(:,3); >> r=X1'*M*X1 >> X1=X1/sqrt(r) >> r=X2'*M*X2; >> X2=X2/sqrt(r); >> r=X3'*M*X3; >> X3=X3/sqrt(r); >> V=[X1,X2,X3];
En el sistema de coordenadas u, que hemos definido mediante la transformación x=V·u, las fuerzas f1(t), f2(t) y f3(t) se expresan
>> syms f w t a positive; >> F=[f*cos(w*t)-k*a;0;k*a]; >> f=V'*F; >> f=simplify(f);
El sistema de ecuaciones diferenciales desacopladas es
Condiciones iniciales
Conocido x1(0), x2(0) y x3(0), obtenemos las condiciones iniciales u1(0), u2(0) y u3(0) mediante la transformación u0=V-1·x0. Se procede del mismo modo para las velocdiades iniciales.
>> u0=inv(V)*[0;a;2*a];
Primera ecuación diferencial
Segunda ecuación diferencial
Tercera ecuación diferencial
Integramos para obtener la velocidad du1/dt, la velocidad inicial es nula
Integramos de nuevo, para obtener la posición u1(t) del primer cuerpo, la posición inicial es
La solución particular es y2=Acos(ωt)+B. Introducimos en la ecuación diferencial para obtener los coeficientes A y B
La solución completa es
Los coeficientes C y D se determinan a partir de las condiciones iniciales,
La primera condición
La segunda
La solución de la segunda ecuación diferencial es
La solución particular es y2=Acos(ωt). Introducimos en la ecuación diferencial para obtener el coeficiente A
La solución completa es
Los coeficientes C y D se determinan a partir de las condiciones iniciales,
Primera condición
Segunda condición
La solución de la tercera ecuación diferencial es
Relacionamos la posición de cada cuerpo xi con ui, mediante la transformación x=V·u
Los posiciones de cada uno de los cuerpos son
x2(t)-a es el desplazamiento del segundo cuerpo de su posición inicial de equilibrio, x3(t)-2a es el desplazamiento del tercer cuerpo de su posición inicial de equilibrio
Referencias
Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1124, pp. 208-211

