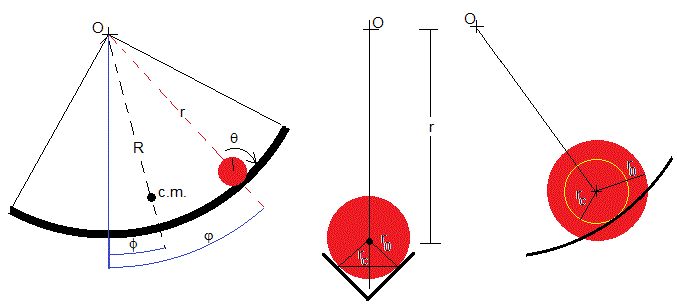
A la izquierda de la figura, se representa una pista de masa M doblada en forma de cuarto de circunferencia cuyos extremos se cuelgan de un punto O mediante hilos. La sección trasversal de la pista tiene forma de V con el vértice de 90°. La bola de masa m y radio r₀ rueda sin deslizar a lo largo de la pista.

Los puntos de contacto de la bola con la pista distan $r_c=r_0/\sqrt{2}$ de su centro. De modo, que la distancia entre el punto O y la línea de rodadura es r+r_c, tal como se muestra a la derecha de la figura.

El centro de la bola describe un arco de circunferencia de radio r y forma un ángulo φ con la dirección vertical. El centro de masas de la pista (punto de color negro) describe un arco de circunferencia de radio R y forma un ángulo ɸ con la dirección vertical tal como se muestra en la figura.

Centro de masa de una pista circular

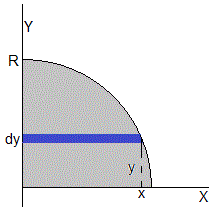
Calculamos primero el centro de masa de una figura homogénea, de densidad constante, en forma de cuarto de círculo de radio R.

${\displaystyle y_{cm}=\frac{{\displaystyle \underset{0}{\overset{R}{\int }}y\left(xdy\right)}}{{\displaystyle \underset{0}{\overset{R}{\int }}xdy}}}$

donde x·dy es el área del rectángulo en color azul.

La relación entre x e y es la ecuación de la circunferencia $x^2+y^2=R^2$. El denominador es el área de un cuarto de círculo, πR²/4

${\displaystyle y_{cm}=\frac{{\displaystyle \underset{0}{\overset{R}{\int }}y\sqrt{R^2-y^2}dy}}{\pi R^2/4}={-\frac{4}{\pi R^2}\frac{1}{3}\left(\sqrt{R^2-y^2}\right)|}_0^R=\frac{4R}{3\pi }}$

Por simetría, x_cm=y_cm. El centro de masas se encuentra a una distancia R del origen en la bisectriz del primer cuadrante $R=y_{cm}\sqrt{2}$

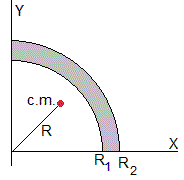
Calculamos ahora, el centro de masas de la pista en forma de cuarto de circunferencia de radio interior R₁ y radio exterior R₂.

${\displaystyle \begin{array}{l}{y}_{cm}=\frac{\left(\pi R_2^2/4\right)\left(4R_2/3\pi \right)-\left(\pi R_1^2/4\right)\left(4R_1/3\pi \right)}{\left(\pi R_2^2/4\right)-\left(\pi R_1^2/4\right)}\\ =\frac{4}{3\pi }\frac{R_2^2+R_1{R}_2+R_1^2}{R_2+R_1}\end{array}}$

Con R₁=19 cm y R₂=20.9 cm, la distancia R desde el punto O al centro de masas de la pista es

${\displaystyle R=\frac{4}{3\pi }\sqrt{2}\frac{R_2^2+R_1{R}_2+R_1^2}{R_2+R_1}}$

R=17.97 cm

Momento de inercia de la pista circular

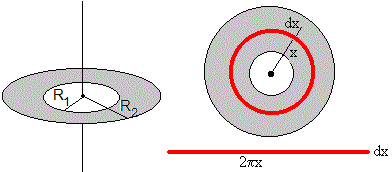
Calculamos el momento de inercia de un disco con un agujero en su centro de masa M y radios interior R₁ y exterior R₂, respecto de un eje perpendicular al plano del disco y que pasa por su centro.

Tomamos un elemento diferencial de masa que dista x del eje de rotación. El elemento es un anillo de radio x y de anchura dx. Si recortamos el anillo y lo extendemos, se convierte en un rectángulo de longitud 2πx y anchura dx, cuya masa es

${\displaystyle dm=\frac{M}{\pi \left(R_2^2-R_1^2\right)}2\pi xdx=\frac{2M}{\left(R_2^2-R_1^2\right)}xdx}$

El momento de inercia disco es

${\displaystyle I_O=\underset{R_1}{\overset{R_2}{{\displaystyle \int }}}\frac{2M}{R_2^2-R_1^2}{x}^{3}dx=\frac{1}{2}\frac{M}{R_2^2-R_1^2}\left(R_2^4-R_1^4\right)=\frac{1}{2}M\left(R_2^2+R_1^2\right)}$

La pista en forma de cuarto de circunferencia tiene de radios interior R₁=19 cm y R₂=19+1.9=20.9 cm, su masa es de M=90 g, por lo que el momento de inercia es I_O=3.59·10^-3 kg m².

Energía cinética y potencial de la pista

El ángulo ɸ mide la posición angular del centro de la pista respecto del eje vertical. En el equilibrio ɸ=0

La pista, de momento de inercia I_O describe un movimiento de rotación con velocidad angular dɸ/dt alrededor de un eje perpendicular al plano de la pista que pasa por O. La energía cinética es

${\displaystyle E_{1k}=\frac{1}{2}{I}_0{\left(\frac{d\varphi }{dt}\right)}^2}$

Situamos el nivel cero de energía potencial en el eje O. Cuando el c.m. de la pista se ha desviado un ángulo ɸ de la vertical, su energía potencial es E_1p=-MgRcosɸ.

Energía cinética y potencial de la bola

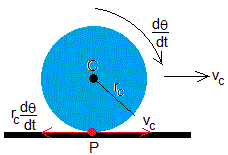
La posición angular del centro de la bola, medida desde la dirección vertical es φ, su velocidad es r·dφ/dt.

Cuando una bola de radio r_c rueda sin deslizar sobre una superficie horizontal, el punto de contacto P está en reposo v_P=0. La velocidad del punto P es la suma de la velocidad de traslación del centro v_c y r_cdθ/dt (de sentido contrario) donde dθ/dt es la velocidad angular de rotación alrededor de un eje perpendicular que pasa por el centro. La relación entre ambas velocidades (traslación y rotación) es v_P=v_c+r_c·dθ/dt=0

Para el observador inercial, la bola se mueve sobre la pista, el punto de contacto P de la bola con la pista describe un arco de circunferencia de radio (r+r_c) con velocidad (r+r_c)·dɸ/dt. El centro de la bola describe un arco de circunferencia de radio r con velocidad rdφ/dt, la relación entre velocidades se escribe

${\displaystyle (r_c+r)\frac{d\varphi }{dt}=r\frac{d\phi }{dr}+r_c\frac{d\theta }{dt}}$

La energía cinética de la bola es la suma de la energía cinética de traslación del centro y la energía cinética de rotación alrededor de un eje que pasa por el centro. Sabiendo que el momento de inercia de una esfera es 2mR²/5.

${\displaystyle E_{2k}=\frac{1}{2}m{\left(r\frac{d\phi }{dt}\right)}^2+\frac{1}{2}\left(\frac{2}{5}m{r}_0^2\right){\left(\frac{d\theta }{dt}\right)}^2}$

Situamos el nivel cero de energía potencial en el eje O. Cuando el centro de la bola se ha desviado un ángulo φ de la vertical su energía potencial es E_2p=-mgrcosφ.

Ecuaciones del movimiento

La energía total E_1k+E_2k+E_1p+E_2p del sistema bola-pista se conserva

${\displaystyle E=\frac{1}{2}{I}_0{\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}m{\left(r\frac{d\phi }{dt}\right)}^2+\frac{1}{2}\left(\frac{2}{5}m{r}_0^2\right){\left(\frac{d\theta }{dt}\right)}^2-MgR\cos \varphi -mgr\cos \phi }$

La energía total se deberá mantener constante e igual a la energía inicial durante todo el movimiento.

Teniendo en cuenta la relación entre las velocidades angulares dɸ/dt, dφ/dt y dθ/dt, deducida en el apartado anterior, la energía del sistema se expresa

${\displaystyle \begin{array}{l}E=\frac{1}{2}{I}_0{\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}m{\left(r\frac{d\phi }{dt}\right)}^2+\frac{1}{2}\left(\frac{2}{5}m{r}_0^2\right){\left(\frac{r_c+r}{r_c}\frac{d\varphi }{dt}-\frac{r}{r_c}\frac{d\phi }{dr}\right)}^2-MgR\cos \varphi -mgr\cos \phi \\ E=\frac{1}{2}\left(I_0+\frac{2}{5}m{r}_0^2{\left(\frac{r_c+r}{r_c}\right)}^2\right){\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}m\left(1+\frac{2}{5}{r}_0^2\frac{1}{r_c^2}\right)r^2{\left(\frac{d\phi }{dt}\right)}^2-\left(\frac{2}{5}m{r}_0^2\right)\frac{r\left(r_c+r\right)}{r_c^2}\frac{d\varphi }{dt}\frac{d\phi }{dt}\\ -MgR\cos \varphi -mgr\cos \phi \end{array}}$

La lagrangiana L=E_k-E_k

${\displaystyle \begin{array}{l}L=\frac{1}{2}\left(I_0+\frac{2}{5}m{r}_0^2{\left(\frac{r_c+r}{r_c}\right)}^2\right){\left(\frac{d\varphi }{dt}\right)}^2+\frac{1}{2}m\left(1+\frac{2}{5}{r}_0^2\frac{1}{r_c^2}\right)r^2{\left(\frac{d\phi }{dt}\right)}^2-\left(\frac{2}{5}m{r}_0^2\right)\frac{r\left(r_c+r\right)}{r_c^2}\frac{d\varphi }{dt}\frac{d\phi }{dt}\\ +MgR\cos \varphi +mgr\cos \phi \end{array}}$

Las ecuaciones del movimiento son,

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{d\dot{\varphi }}\right)-\frac{\partial L}{d\varphi }=0\\ \left(I_0+\frac{2}{5}m{r}_0^2{\left(\frac{r_c+r}{r_c}\right)}^2\right)\frac{d^2\varphi }{d{t}^2}-\left(\frac{2}{5}m{r}_0^2\right)\frac{r\left(r_c+r\right)}{r_c^2}\frac{d^2\phi }{d{t}^2}+MgR\sin \varphi =0\\ \frac{d}{dt}\left(\frac{\partial L}{d\dot{\phi }}\right)-\frac{\partial L}{d\phi }=0\\ m\left(1+\frac{2}{5}{r}_0^2\frac{1}{r_c^2}\right)r^2\frac{d^2\phi }{d{t}^2}-\left(\frac{2}{5}m{r}_0^2\right)\frac{r\left(r_c+r\right)}{r_c^2}\frac{d^2\varphi }{d{t}^2}+mgr\sin \phi =0\end{array}}$

Tenemos que resolver el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}B\frac{d^2\varphi }{d{t}^2}-C\frac{d^2\phi }{d{t}^2}+MgR\sin \varphi =0\\ D\frac{d^2\phi }{d{t}^2}-C\frac{d^2\varphi }{d{t}^2}+mgr\sin \phi =0\end{array}\\ B=I_0+\frac{2}{5}m{r}_0^2{\left(\frac{r_c+r}{r_c}\right)}^{2}C=\left(\frac{2}{5}m{r}_0^2\right)\frac{r\left(r_c+r\right)}{r_c^2}D=m{r}^2+\frac{2}{5}m{r}_0^2\frac{r^2}{r_c^2}\end{array}}$

Con las condiciones iniciales siguientes: En el instante t=0, la bola y la pista parten del reposo, dφ/dt=0 y dɸ/dt=0, desde las posiciones ɸ=ɸ₀ y φ=φ₀.

Para integrar el sistema de dos ecuaciones difrenciales, despejamos las derivadas segundas de los ángulos φ y ɸ en el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^2\varphi }{d{t}^2}+\frac{D·MgR\sin \varphi +C·mgr\sin \phi }{BD-C^2}=0\\ \frac{d^2\phi }{d{t}^2}+\frac{C·MgR\sin \varphi +B·mgr\sin \phi }{BD-C^2}=0\end{array}}$

Resolvemos el sistema de dos ecuaciones diferenciales de segundo orden utilizando el procedimiento ode45 de MATLAB. En el instante t=0, se desvía la bola un ángulo φ₀=π/6 (30°), la pista no se desvía, ɸ₀=0 y se suelta. La bola y la pista oscilan, representándose las posiciones angulares del c.m. de la pista ɸ y del centro de la bola φ en función del tiempo t

Con los datos que aparecen al principio del script:

• Momento de inercia de la pista, I=3.59·10^-3 kgm²
• Masa de la pista, M= 90 g
• El centro de masas de la pista describe un arco de circunferencia de radio, R=17.97 cm
• Radio de la bola, r₀= 1.27 cm
• Masa de la bola, m=67 g
• Distancia entre el centro de la bola y la pista, r_c=0.898 cm
• El centro de la bola describe un arco de circunferencia de radio, r=18.4 cm

I=3.59e-3;  %momento de inercia de la pista
M=0.090; %masa de la pista
r0=1.27/100; %radio de la bola
m=0.067; %masa de la bola
rc=r0/sqrt(2); %contacto bola-pista
r=18.4/100; %radio del centro de la bola
R=17.97/100; %centro de masas de la pista

%coeficientes
B=I+2*m*r0^2*(rc+r)^2/(5*rc^2);
C=2*m*r0^2*r*(r+rc)/(5*rc^2);
D=m*r^2+2*m*r0^2*r^2/(5*rc^2);

%condiciones iniciales
xPista=0;
xBola=pi/6;
%xPista=10*pi/180;  
%xBola=11.5566*pi/180;  %modo normal 1
%xBola=-10.8690*pi/180; %modo normal 2
% x(3) es phi, x(4) es dphi/dt, x(1) es rh, x(2) es drh/dt
fg=@(t,x)[x(2);(D*M*9.8*R*sin(x(1))+C*m*9.8*r*sin(x(3)))/(C^2-B*D); x(4); 
(C*M*9.8*R*sin(x(1))+B*m*9.8*r*sin(x(3)))/(C^2-B*D)];
[t,x]=ode45(fg,[0,10],[xPista,0,xBola,0]); % la bola se desvía un radián
hold on
plot(t,x(:,1)) 
plot(t,x(:,3)) 
hold off
grid on
legend('pista','bola', 'location','southeast');
ylabel('angulos')
xlabel('t')
title('Bola rueda sobre pista')

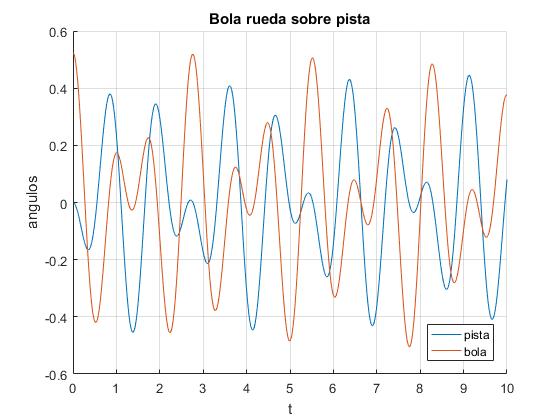
Añadimos al script, el cálculo de la energía inicial E₀ y de la energía en cualquier instante E. El mayor tanto por ciento de error, $\text{max}\left(\left|\frac{E-E_0}{E_0}\right|\times 100\right)$, es muy pequeño, de este modo, verificamos el procedimiento numérico

...
Einicial=-m*9.8*r*cos(xBola)-M*9.8*R; % la bola se desvía un radián
E=I*x(:,2).^2/2+m*r^2*x(:,4).^2/2+(m*r0^2/5)*((rc+r)*x(:,2)/rc-r*x(:,4)/rc).^2
-M*9.8*R*cos(x(:,1))-m*9.8*r*cos(x(:,3));
max(abs(100*(Einicial-E)/Einicial)) 
%error máximo en el intervalo de tiempo especificado

ans =    0.0980

Para las siguientes condiciones iniciales, en comentarios en el código, observamos los modos normales de vibración:

• Primer modo normal de vibración: ɸ₀=10·π/180 (10 grados), φ₀=11.5566·π/180
• Segundo modo normal de vibración: ɸ₀=10·π/180 (10 grados), φ₀=-10.8690·π/180

Modos normales de vibración

Si nos restringimos a pequeños valores de los ángulos sinφ≈φ y sinɸ≈ɸ, el sistema de ecuaciones diferenciales se transforma en

${\displaystyle \{\begin{array}{l}B\frac{d^2\varphi }{d{t}^2}-C\frac{d^2\phi }{d{t}^2}+MgR\varphi =0\\ D\frac{d^2\phi }{d{t}^2}-C\frac{d^2\varphi }{d{t}^2}+mgr\phi =0\end{array}}$

Ensayamos una solución de la forma ɸ=A₁sin(ωt), φ=A₂sin(ωt)

${\displaystyle \begin{array}{l}\{\begin{array}{l}-{\omega }^{2}B{A}_1+{\omega }^{2}C{A}_2+MgR{A}_1=0\\ -{\omega }^{2}D{A}_2+{\omega }^{2}C{A}_1+mgr{A}_2=0\end{array}\\ \{\begin{array}{l}\left(MgR-{\omega }^{2}B\right)A_1+\left({\omega }^{2}C\right)A_2=0\\ \left(mgr-{\omega }^{2}D\right)A_2+\left({\omega }^{2}C\right)A_1=0\end{array}\end{array}}$

Se trata de un sistema homogéneo de dos ecuaciones con dos incógnitas, por lo que

${\displaystyle \begin{array}{l}{\omega }^4{C}^2+\left(MgR-{\omega }^{2}B\right)\left(mgr-{\omega }^{2}D\right)=0\\ {\omega }_1^2=\frac{\left(MgRD+mgrB\right)+\sqrt{{\left(MgRD+mgrB\right)}^2-4\left(BD-C^2\right)Mm{g}^{2}Rr}}{2\left(BD-C^2\right)}\\ {\omega }_2^2=\frac{\left(MgRD+mgrB\right)-\sqrt{{\left(MgRD+mgrB\right)}^2-4\left(BD-C^2\right)Mm{g}^{2}Rr}}{2\left(BD-C^2\right)}\end{array}}$

La forma general de la posición angular ɸ del centro de masas de la pista, en función del tiempo t es una combinación de los dos modos normales de vibración

ɸ(t)=A₁sin(ω₁t)+ B₁cos(ω₁t)+ C₁sin(ω₂t)+ D₁cos(ω₂t)

Lo mismo para la posición angular del centro de la bola, φ

φ(t)=A₂sin(ω₁t)+ B₂cos(ω₁t)+ C₂sin(ω₂t)+ D₂cos(ω₂t)

Derivando con respecto del tiempo obtenemos la expresión de las velocidades angulares

${\displaystyle \begin{array}{l}\frac{d\varphi }{dt}={\omega }_1\left(A_1\cos ({\omega }_{1}t)-B_1\sin ({\omega }_{1}t)\right)+{\omega }_2\left(C_1\cos ({\omega }_{2}t)-D_1\sin ({\omega }_{2}t)\right)\hfill \\ \frac{d\phi }{dt}={\omega }_1\left(A_2\cos ({\omega }_{1}t)-B_2\sin ({\omega }_{1}t)\right)+{\omega }_2\left(C_2\cos ({\omega }_{2}t)-D_2\sin ({\omega }_{2}t)\right)\hfill \end{array}}$

Las condiciones iniciales en el instante

${\displaystyle t=0\{\begin{array}{l}\varphi ={\varphi }_0,\frac{d\varphi }{dt}=0\\ \phi ={\phi }_0,\frac{d\phi }{dt}=0\end{array}}$

dan lugar a cuatro ecuaciones

${\displaystyle \{\begin{array}{l}{B}_1+D_1={\varphi }_0\\ {\omega }_1{A}_1+{\omega }_2{C}_1=0\\ B_2+D_2={\phi }_0\\ {\omega }_1{A}_2+{\omega }_2{C}_2=0\end{array}}$

Derivando las velocidades angulares, obtenemos las aceleraciones angulares

${\displaystyle \begin{array}{l}\frac{d^2\varphi }{d{t}^2}=-{\omega }_1^2\left(A_1\sin ({\omega }_{1}t)+B_1\sin ({\omega }_{1}t)\right)-{\omega }_2^2\left(C_1\sin ({\omega }_{2}t)+D_1\cos ({\omega }_{2}t)\right)\hfill \\ \frac{d^2\phi }{d{t}^2}=-{\omega }_1^2\left(A_2\sin ({\omega }_{1}t)+B_2\sin ({\omega }_{1}t)\right)-{\omega }_2^2\left(C_2\sin ({\omega }_{2}t)+D_2\cos ({\omega }_{2}t)\right)\hfill \end{array}}$

Relacionamos los coeficientes A₁ y A₂, B₁ y B₂, C₁ y C₂, D₁ y D₂, calculando la derivada segunda de ɸ, la derivada segunda de φ e introduciéndolos en una de las dos ecuaciones diferenciales del movimiento

${\displaystyle D\frac{d^2\phi }{d{t}^2}-C\frac{d^2\varphi }{d{t}^2}+mgr\phi =0}$

Llegamos a otras cuatro relaciones

${\displaystyle \{\begin{array}{l}\left(-D{\omega }_1^2+mgr\right)A_2+C{\omega }_1^2{A}_1=0\\ \left(-D{\omega }_1^2+mgr\right)B_2+C{\omega }_1^2{B}_1=0\\ \left(-D{\omega }_2^2+mgr\right)C_2+C{\omega }_2^2{C}_1=0\\ \left(-D{\omega }_2^2+mgr\right)D_2+C{\omega }_2^2{D}_1=0\end{array}}$

En el sistema de ocho ecuaciones con ocho incógnitas, despejamos los coeficientes, A₁, A₂, B₁, B₂, C₁, C₂, D₁ y D₂

Lo primero que vemos son los coeficientes que se hacen nulos

${\displaystyle \begin{array}{l}{C}_1=0C_2=0\\ A_1=0A_2=0\end{array}}$

quedando reducido el sistema a cuatro ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left(-D{\omega }_1^2+mgr\right)B_2+C{\omega }_1^2{B}_1=0\\ \left(-D{\omega }_2^2+mgr\right)D_2+C{\omega }_2^2{D}_1=0\end{array}\\ \{\begin{array}{l}{B}_1+D_1={\varphi }_0\\ B_2+D_2={\phi }_0\end{array}\end{array}}$

cuya solución es

${\displaystyle \begin{array}{l}{B}_2=\frac{{\omega }_1^2}{mgr\left({\omega }_1^2-{\omega }_2^2\right)}\left\{\left(-D{\omega }_2^2+mgr\right){\phi }_0+C{\omega }_2^2{\varphi }_0\right\}{B}_1=-\frac{-D{\omega }_1^2+mgr}{C{\omega }_1^2}{B}_2\\ D_2=-\frac{{\omega }_2^2}{mgr\left({\omega }_1^2-{\omega }_2^2\right)}\left\{\left(-D{\omega }_1^2+mgr\right){\phi }_0+C{\omega }_1^2{\varphi }_0\right\}{D}_1=-\frac{-D{\omega }_2^2+mgr}{C{\omega }_2^2}{D}_2\end{array}}$

Las posiciones angulares en función del tiempo t del centro de masas de la pista y del centro de la bola son:

ɸ(t)=B₁cos(ω₁t)+ D₁cos(ω₂t)
φ(t)=B₂cos(ω₁t)+D₂cos(ω₂t)

Modos normales de vibración

• El modo 1 de frecuencia angular ω₁, se obtiene cuando D₂=0 y por tanto, D₁=0. La relación entre los ángulos iniciales de desviación es

${\displaystyle {\phi }_0=\frac{C{\omega }_1^2}{D{\omega }_1^2-mgr}{\varphi }_0}$

La posición angular en función del tiempo t es

ɸ(t)=ɸ₀cos(ω₁t)
φ(t)=φ₀cos(ω₁t)

• El modo 2 de frecuencia angular ω₂, se obtiene cuando B₂=0 y por tanto, B₁=0. La relación entre los ángulos iniciales de desviación es

${\displaystyle {\phi }_0=\frac{C{\omega }_2^2}{D{\omega }_2^2-mgr}{\varphi }_0}$

La posición angular en función del tiempo t es

ɸ(t)=ɸ₀cos(ω₂t)
φ(t)=φ₀cos(ω₂t)

Con los mismos datos que aparecen al principio del script y que hemos utilizado anteriormente. Calculamos las frecuencias ω₁ y ω₂ de los modos normales de vibración

Si desplazamos la pista ɸ₀= 10·180/π (10 grados)

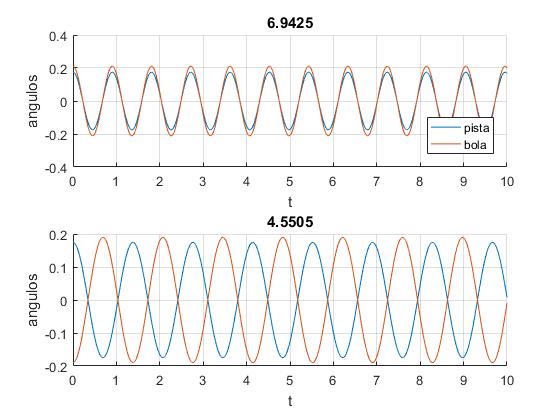
• El primer modo de frecuencia ω₁, se observa cuando el centro de la bola se desplaza φ₀=0.2107 (11.56 grados)
• El segundo modo de frecuencia ω₂, se observa cuando el centro de la bola se desplaza φ₀=-0.1897 (-10.87 grados)

Representamos los dos modos de vibración, en el título de cada uno de los gráficos se proporciona la frecuencia angular

I=3.59e-3;  %momento de inercia de la pista
M=0.090; %masa de la pista
r0=1.27/100; %radio de la bola
m=0.067; %masa de la bola
rc=r0/sqrt(2); %contacto bola-pista
r=18.4/100; %radio del centro de la bola
R=17.97/100; %centro de masas de la pista

%coeficientes
B=I+2*m*r0^2*(rc+r)^2/(5*rc^2);
C=2*m*r0^2*r*(r+rc)/(5*rc^2);
D=m*r^2+2*m*r0^2*r^2/(5*rc^2);

%frecuencias de los modos normales de oscilación
w1=sqrt((M*9.8*R*D+m*9.8*r*B+sqrt((M*9.8*R*D+m*9.8*r*B)^2-
4*(B*D-C^2)*M*m*9.8^2*R*r))/(2*(B*D-C^2)));
w2=sqrt((M*9.8*R*D+m*9.8*r*B-sqrt((M*9.8*R*D+m*9.8*r*B)^2-
4*(B*D-C^2)*M*m*9.8^2*R*r))/(2*(B*D-C^2)));

%ángulo inicial de la pista
rh_0=10*pi/180;

%primer modo, frecuencia w1
phi_0=C*w1^2*rh_0/(D*w1^2-m*9.8*r); %ángulo de la bola
subplot(2,1,1)
hold on
fplot(@(t) rh_0*cos(w1*t),[0,10])
fplot(@(t) phi_0*cos(w1*t),[0,10])
hold off
grid on
xlabel('t')
ylabel('angulos')
legend('pista','bola', 'location','southeast');
title(num2str(w1))

%segundo modo, frecuencia w2
phi_0=C*w2^2*rh_0/(D*w2^2-m*9.8*r); %ángulo de la bola
subplot(2,1,2)
hold on
fplot(@(t) rh_0*cos(w2*t),[0,10])
fplot(@(t) phi_0*cos(w2*t),[0,10])
hold off
grid on
xlabel('t')
ylabel('angulos')
title(num2str(w2))

Actividades

Se han fijado los siguientes parámetros:

• Momento de inercia de la pista, I=3.59·10^-3 kgm²
• Masa de la pista, M= 90 g
• El centro de masas de la pista describe un arco de circunferencia de radio, R=17.97 cm
• Radio de la bola, r₀= 1.27 cm
• Masa de la bola, m=67 g
• Distancia entre el centro de la bola y la pista, r_c=0.898 cm
• El centro de la bola describe un arco de circunferencia de radio, r=18.4 cm

Se introduce

• El ángulo inicial de desviación de la pista, ɸ₀ en grados, en el control titulado Angulo pista
• El ángulo inicial de desviación de la bola, φ₀ en grados, en el control titulado Angulo bola

Se pulsa el botón titualdo Nuevo

Se observa el movimiento oscilatorio de la pista y la bola rodando sobre la pista

Si activamos la casilla titulada Gráfica y pulsamos el botón titulado Nuevo, observamos la representación gráfica de los ángulos de desviación de la pista ɸ (en azul) y de la bola φ (en rojo) medidos desde la vertical, en función del tiempo t

Cuando desplazamos la pista, ɸ₀= 10·180/π (10 grados)

Se resuelve el sistema de ecuaciones diferenciales por el procedimiento de Runge-Kutta. Se compara la energía inicial con la energía del sistema en cada instante. Se calcula y se muestra el error, que hemos definido en la primera sección y que se debrá se casi nulo

• El primer modo de frecuencia ω₁, se observa cuando el centro de la bola se desplaza φ₀=0.2107 (11.56 grados)
• El segundo modo de frecuencia ω₂, se observa cuando el centro de la bola se desplaza φ₀=-0.1897 (-10.87 grados)

Referencias

R. E. Benenson, B. B. Marsh. Coupled oscillations of a ball and curved-track pendulum. Am. J. Phys. 56 (4) April 1988. pp. 345-348