Con rozamiento

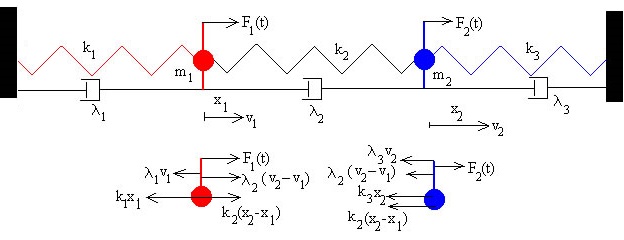
En la parte inferior de la figura, se muestran mediante vectores las fuerzas que actúan sobre cada una de las partículas, fijarse en aquellas que corresponden a las interacciones mutuas.

${\displaystyle \begin{array}{l}\{\begin{array}{l}{m}_1\frac{d^2{x}_1}{d{t}^2}=F_1(t)+k_2(x_2-x_1)+{\lambda }_2\left(v_2-v_1\right)-k_1{x}_1-{\lambda }_1{v}_1\\ m_2\frac{d^2{x}_2}{d{t}^2}=F_2(t)-k_2(x_2-x_1)-{\lambda }_2\left(v_2-v_1\right)-k_3{x}_2-{\lambda }_3{v}_2\end{array}\\ \{\begin{array}{l}{m}_1\frac{d^2{x}_1}{d{t}^2}+\left({\lambda }_1+{\lambda }_2\right)\frac{d{x}_1}{dt}-{\lambda }_2\frac{d{x}_2}{dt}+\left(k_1+k_2\right)x_1-k_2{x}_2=F_1(t)\\ m_2\frac{d^2{x}_2}{d{t}^2}-{\lambda }_2\frac{d{x}_1}{dt}+\left({\lambda }_2+{\lambda }_3\right)\frac{d{x}_2}{dt}-k_2{x}_1+\left(k_2+k_3\right)x_2=F_2(t)\end{array}\end{array}}$

En forma matricial escribimos

${\displaystyle \begin{array}{l}\left(\begin{array}{cc}{m}_1& 0\\ 0& m_2\end{array}\right)\left(\begin{array}{c}\frac{d^2{x}_1}{d{t}^2}\\ \frac{d^2{x}_2}{d{t}^2}\end{array}\right)+\left(\begin{array}{cc}{\lambda }_1+{\lambda }_2& -{\lambda }_2\\ -{\lambda }_2& {\lambda }_2+{\lambda }_3\end{array}\right)\left(\begin{array}{c}\frac{d{x}_1}{dt}\\ \frac{d{x}_2}{dt}\end{array}\right)+\\ \left(\begin{array}{cc}{k}_1+k_2& -k_2\\ -k_2& k_2+k_3\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{F}_1(t)\\ F_2(t)\end{array}\right)\end{array}}$

Donde M, C y K son las matrices simétricas masa, rozamiento y constantes de los muelles.

Calculamos los valores propios y los vectores propios de la matriz M^-1·K.

>> [V,D]=eig(inv(M)*K)

La matriz diagonal D contiene en su diagonal principal los cuadrados de las frecuencias de los modos normales de vibración, ω₁ y ω₂.

Los vectores columna de la matriz V son los vectores propios correspondientes a cada uno de los valores propios. Modificamos la matriz V multiplicando cada vector propio por un factor de escala, de modo que se cumpla

${\displaystyle \begin{array}{l}{M}_g={\left(V\right)}^T·M·V=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\\ K_g={\left(V\right)}^T·K·V=\left(\begin{array}{cc}{\omega }_1^2& 0\\ 0& {\omega }_2^2\end{array}\right)\end{array}}$

Definimos un espacio u(t) de modo que

${\displaystyle \begin{array}{l}x(t)=V·u(t)\\ \dot{x}(t)=V·\dot{u}(t)\\ \ddot{x}(t)=V·\ddot{u}(t)\end{array}}$

La ecuación diferencial del movimiento en forma vectorial se transforma en

${\displaystyle \begin{array}{l}M·V·\ddot{u}(t)+CV·\dot{u}(t)+KV·u(t)=F\\ {\left(V\right)}^T·M·V·\ddot{u}(t)+{\left(V\right)}^T·CV·\dot{u}(t)+{\left(V\right)}^T·KV·u(t)={\left(V\right)}^T·F\\ M_g·\ddot{u}(t)+C_g·\dot{u}(t)+K_g·u(t)=f(t)\\ M_g=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)K_g=\left(\begin{array}{cc}{\omega }_1^2& 0\\ 0& {\omega }_2^2\end{array}\right)C_g={\left(V\right)}^T·CV\end{array}}$

El problema que aparece ahora es que la matriz C_g habitualmente no es diagonal, con los cual no se pueden desacoplar las ecuaciones diferenciales del movimiento de las partículas.

Ejemplo

Continuando con el ejemplo del apartado anterior: Sea el sistema de dos partículas de masas m₁=2 y m₂=1, unidas por muelles de constantes k₁=6, k₂=3 y k₃=0. Sobre la segunda partícula actúa una fuerza de la forma F₂(t)=2·cos(ω_f t), sobre la primera no actúa ninguna fuerza F₁(t)=0. Los coeficientes de las fuerza de rozamiento son: λ₁=λ₂=1, λ₃=0

${\displaystyle \begin{array}{l}\left(\begin{array}{cc}2& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}\frac{d^2{x}_1}{d{t}^2}\\ \frac{d^2{x}_2}{d{t}^2}\end{array}\right)+\left(\begin{array}{cc}2& -1\\ -1& 1\end{array}\right)\left(\begin{array}{c}\frac{d{x}_1}{dt}\\ \frac{d{x}_2}{dt}\end{array}\right)+\left(\begin{array}{cc}9& -3\\ -3& 6\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ =\left(\begin{array}{c}0\\ 2·\cos ({\omega }_{f}t)\end{array}\right)\end{array}}$

syms t wf;
M=sym([2,0;0,1]);
K=sym([9,-3;-3,3]);
C=sym([2,-1;-1,1]);
[V,D]=eig(inv(M)*K);
W=diag(sqrt(D)); %vector de las frecuencias propias
%calcula una nueva matriz V
for i=1:length(W)
    r=V(:,i)'*M*V(:,i);
    V(:,i)=V(:,i)/sqrt(r);
end

%comprobación
Mg=V'*M*V
Kg=V'*K*V
Cg=V'*C*V
%vector fuerza
F=sym([0;2*cos(wf*t)]);
f=V'*F

En la ventana de comandos vemos que M_g y K_g son matrices diagonales pero no lo es C_g

Mg =
[ 1, 0]
[ 0, 1]
Kg =
[ 3/2, 0]
[   0, 6]
Cg =
[       1/3, 2^(1/2)/6]
[ 2^(1/2)/6,       5/3]
f =
 (2*2^(1/2)*3^(1/2)*cos(t*wf))/3
         (2*3^(1/2)*cos(t*wf))/3
>> V
V = 
[ (2^(1/2)*3^(1/2))/6, -3^(1/2)/3]
[ (2^(1/2)*3^(1/2))/3,  3^(1/2)/3]

${\displaystyle C_g=\left(\begin{array}{cc}\frac{1}{3}& \frac{\sqrt{2}}{6}\\ \frac{\sqrt{2}}{6}& \frac{5}{3}\end{array}\right)}$

La matriz C_g se diagonaliza mediante el procedimiento denominado balance de energía, que viene descrito en textos de Vibraciones Mecánicas.

${\displaystyle C_g=\left(\begin{array}{cc}{c}_1& 0\\ 0& c_2\end{array}\right)c_1=\frac{{\left(X_1\right)}^T·C·X_1}{{\left(X_1\right)}^T·X_1}{c}_2=\frac{{\left(X_2\right)}^T·C·X_2}{{\left(X_2\right)}^T·X_2}}$

donde X₁ y X₂ son los vectores columna de la matriz V de los vectores propios modificada, que hemos calculado anteriormente.

${\displaystyle V=\left(\begin{array}{cc}\frac{\sqrt{6}}{6}& -\frac{\sqrt{3}}{3}\\ \frac{\sqrt{6}}{3}& \frac{\sqrt{3}}{3}\end{array}\right)}$

>> V(:,1)'*C*V(:,1)/(V(:,1)'*V(:,1))
ans =2/5
>> V(:,2)'*C*V(:,2)/(V(:,2)'*V(:,2))
ans =5/2

Se ha hecho la matriz C_g diagonal

${\displaystyle C_g=\left(\begin{array}{cc}\frac{2}{5}& 0\\ 0& \frac{5}{2}\end{array}\right)}$

Las nuevas ecuaciones diferenciales desacopladas en el espacio u son

${\displaystyle \begin{array}{l}\frac{d^2{u}_1}{d{t}^2}+\frac{2}{5}\frac{d{u}_1}{dt}+\frac{3}{2}{u}_1=\frac{2\sqrt{6}}{3}\cos ({\omega }_{f}t)\\ \frac{d^2{u}_2}{d{t}^2}+\frac{5}{2}\frac{d{u}_2}{dt}+6u_2=\frac{2\sqrt{3}}{3}\cos ({\omega }_{f}t)\end{array}}$

Las condiciones iniciales en el espacio u se escriben en forma matricial

${\displaystyle \begin{array}{l}u(0)={\left(V\right)}^T·M·x(0)\\ \dot{u}(0)={\left(V\right)}^T·M·\dot{x}(0)\end{array}}$

En el estado estacionario, la soluciones particulares de estas ecuaciones diferenciales tienen la forma

u_i=A_uicos(ω_f t)+B_uisin(ω_f t), i=1,2

Obtendremos los valores de A_ui y B_ui haciendo que cumpla cada una de las ecuaciones diferenciales

${\displaystyle \begin{array}{l}{A}_{\mathrm{u1}}=\frac{\frac{2\sqrt{6}}{3}\left(\frac{3}{2}-{\omega }_f^2\right)}{{\left(\frac{3}{2}-{\omega }_f^2\right)}^2+{\left(\frac{2}{5}{\omega }_f\right)}^2}{B}_{\mathrm{u1}}=\frac{\frac{2\sqrt{6}}{3}\left(\frac{2}{5}{\omega }_f\right)}{{\left(\frac{3}{2}-{\omega }_f^2\right)}^2+{\left(\frac{2}{5}{\omega }_f\right)}^2}\\ A_{\mathrm{u2}}=\frac{\frac{2\sqrt{3}}{3}\left(6-{\omega }_f^2\right)}{{\left(6-{\omega }_f^2\right)}^2+{\left(\frac{5}{2}{\omega }_f\right)}^2}{B}_{\mathrm{u2}}=\frac{\frac{2\sqrt{3}}{3}\left(\frac{5}{2}{\omega }_f\right)}{{\left(6-{\omega }_f^2\right)}^2+{\left(\frac{5}{2}{\omega }_f\right)}^2}\end{array}}$

Mediante la transformación x=V·u, obtenemos las posiciones x₁(t) y x₂(t) de cada una de las dos partículas en función del tiempo

x_i=A_xicos(ω_f t)+B_xisin(ω_f t), i=1,2

Amplitud de las oscilaciones en función de la frecuencia ω_f

La amplitud A_i de la oscilación de cada una de las partículas es

${\displaystyle A_i=\sqrt{A_{xi}^2+B_{xi}^2}}$

Elaboramos un script que nos permita experimentar con distintos valores de los coeficientes de la fuerza de rozamiento λ₁=λ₂=c, λ₃=0.

syms t wf c;
M=sym([2,0;0,1]);
K=sym([9,-3;-3,3]);
C=sym([2*c,-c;-c,c]);
C=subs(C,c,sym(0.1));

[V,D]=eig(inv(M)*K);
W=diag(sqrt(D)); %vector de frecuencias propias
%calcula una nueva matriz V
for i=1:length(W)
    r=V(:,i)'*M*V(:,i);
    V(:,i)=V(:,i)/sqrt(r);
end
%vector fuerza
F0=sym([0;2]);
f0=V'*F0;
n=length(M);
for i=1:n
    Cg(i,i)= V(:,i)'*C*V(:,i)/(V(:,i)'*V(:,i));
    A(i)=f0(i)*(D(i,i)-wf^2)/((D(i,i)-wf^2)^2+(Cg(i,i)*wf)^2);
    B(i)=f0(i)*Cg(i,i)*wf/((D(i,i)-wf^2)^2+(Cg(i,i)*wf)^2);
    %u(i)=A(i)*cos(wf*t)+B(i)*sin(wf*t);
end
Ax=V*[A',B'];

hold on
color=['b','r','g'];
for i=1:n
    modulo(i)=sqrt(dot(Ax(i,:),Ax(i,:)));
    h=ezplot(modulo(i),[0,3]);
    set(h,'color',color(i))
end
title('Amplitudes')
ylabel('A1,A2')
xlabel('\omega_f')
grid on
hold off

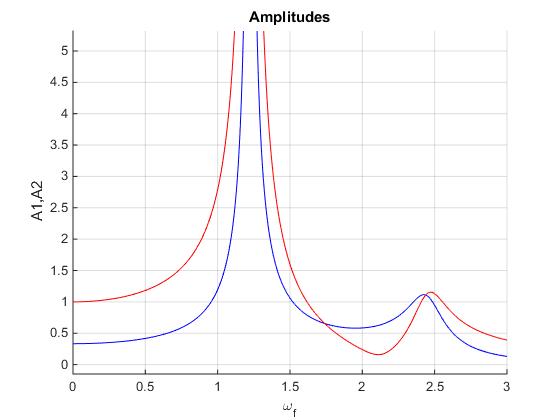
Por ejemplo para c=0.1 (figura más abajo) observamos dos picos, el primero muy agudo próximo a la frecuencia ω₁=1.22 y otro muy pequeño próximo a la frecuencia ω₂=2.45. Este segundo pico, desaparece cuando se incrementa el rozamiento, por ejemplo para c=1.

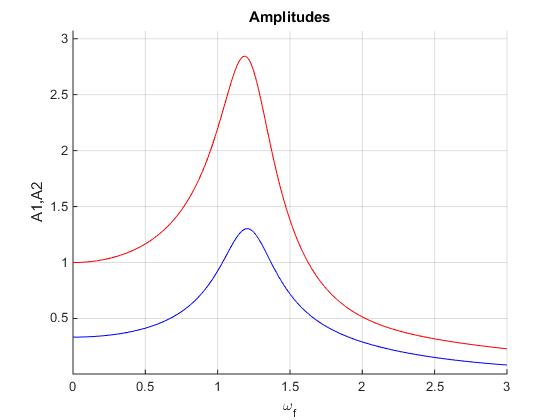
Para c=1

Se cambia la línea de código, C=subs(C,c,sym(1));

Posición de las partículas en función del tiempo

El siguiente script nos permite representar las posiciones x₁(t) y x₂(t) de cada una de las dos partículas en el estado estacionario en función del tiempo para una frecuencia de la fuerza oscilante ω_f

syms t wf c;
M=sym([2,0;0,1]);
K=sym([9,-3;-3,3]);
C=sym([2*c,-c;-c,c]);
C=subs(C,c,sym(1)); %cambiar el rozamiento c

[V,D]=eig(inv(M)*K);
%calcula una nueva matriz V
for i=1:length(W)
    r=V(:,i)'*M*V(:,i);
    V(:,i)=V(:,i)/sqrt(r);
end
%vector fuerza
F0=sym([0;2]);
f0=V'*F0;

n=length(M);
for i=1:n
    Cg(i,i)= V(:,i)'*C*V(:,i)/(V(:,i)'*V(:,i));
    A(i)=f0(i)*(D(i,i)-wf^2)/((D(i,i)-wf^2)^2+(Cg(i,i)*wf)^2);
    B(i)=f0(i)*Cg(i,i)*wf/((D(i,i)-wf^2)^2+(Cg(i,i)*wf)^2);
    u(i)=A(i)*cos(wf*t)+B(i)*sin(wf*t);
end
x=V*u';

 %cambiar la frecuencia wf de la fuerza oscilante
 x=subs(x,wf,sym(sqrt(3/2)));
%representación gráfica
color=['b','r','g'];
hold on
for i=1:n
    h=ezplot(x(i),[0,12]);
    set(h,'color',color(i))
end
title('Dos osciladores acoplados, forzados')
ylabel('x1,x2')
xlabel('t')
grid on
hold off

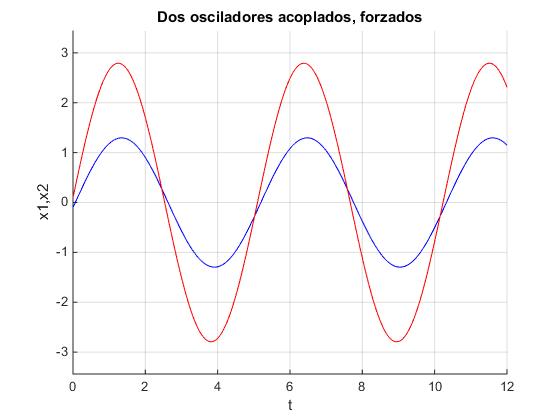
Para la frecuencia ω_f=ω₁ y para c=1, obtenemos la siguiente representación gráfica

El estado transitorio y su evolución hacia el estado estacionario

En el siguiente script resolvemos la ecuación diferencial de cada oscilador en el espacio u, donde las ecuaciones diferenciales del movimiento de cada partícula están desacopladas, del mismo modo que se hizo para las oscilaciones forzadas.

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}+2g\frac{dy}{dt}+{\omega }_0^{2}y=f_{ci}\cos ({\omega }_{f}t)\\ y=u_i{\omega }_0^2=D(i,i)2g=C_g(i,i)f_{ci}=f0(i)\\ y_0=u_i(0)\dot{y}(0)={\dot{u}}_i(0)\end{array}}$

El coeficiente de rozamiento se ha establecido en c=1, la frecuencia de la fuerza oscilante en ${\omega }_f={\omega }_1=\sqrt{\frac{3}{2}}$

syms t wf c;
M=sym([2,0;0,1]);
K=sym([9,-3;-3,3]);
C=sym([2*c,-c;-c,c]);
C=subs(C,c,sym(1)); %cambiar el rozamiento c

[V,D]=eig(inv(M)*K);
W=diag(sqrt(D)); %vector de frecuencias propias
%calcula una nueva matriz V
for i=1:length(W)
    r=V(:,i)'*M*V(:,i);
    V(:,i)=V(:,i)/sqrt(r);
end
%la matriz C se hace diagonal
n=length(M);
for i=1:n
    Cg(i,i)= V(:,i)'*C*V(:,i)/(V(:,i)'*V(:,i));
end
%vector fuerza
F0=sym([0;2]);
f0=V'*F0;

%condiciones iniciales
x0=sym([0;0]);
xp0=sym([0;0]);
u0=V'*M*x0;
up0=V'*M*xp0;

%resuelve las ecuaciones diferenciales desacopladas
syms g fc w0 y0 v0;
eq='D2y+2*g*Dy+w0^2*y=fc*cos(wf*t)';
y=dsolve(eq,'y(0)=y0','Dy(0)=v0');
for i=1:n
    u(i)=subs(y,{g w0 fc y0 v0},{Cg(i,i)/2 W(i) f0(i) u0(i) up0(i)});
end
x=V*u';
%cambiar la frecuencia de la fuerza oscilante
x=subs(x,wf,sym('sqrt(3/2)')) 

%representación gráfica
color=['b','r','g'];
hold on
for i=1:n
    h=ezplot(x(i),[0,30]);
    set(h,'color',color(i))
end
title('Dos osciladores acoplados, forzados')
ylabel('x1,x2')
xlabel('t')
grid on
hold off

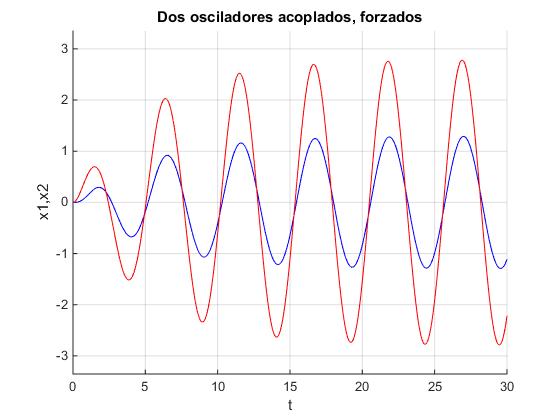
Resolución numérica de las ecuaciones del movimiento

Elaboramos el siguiente script para resolver el sistema de ecuaciones diferenciales que describe el movimiento de cada partícula, con las condiciones iniciales especificadas

${\displaystyle \begin{array}{l}\frac{d^2{x}_1}{d{t}^2}=-\frac{\left({\lambda }_1+{\lambda }_2\right)}{m_1}\frac{d{x}_1}{dt}+\frac{{\lambda }_2}{m_1}\frac{d{x}_2}{dt}-\frac{\left(k_1+k_2\right)}{m_1}{x}_1+\frac{k_2}{m_1}{x}_2+\frac{F_1(t)}{m_1}\\ \frac{d^2{x}_2}{d{t}^2}=\frac{{\lambda }_2}{m_2}\frac{d{x}_1}{dt}-\frac{\left({\lambda }_2+{\lambda }_3\right)}{m_2}\frac{d{x}_2}{dt}+\frac{k_2}{m_2}{x}_1-\frac{\left(k_2+k_3\right)}{m_2}{x}_2+\frac{F_2(t)}{m_2}\\ t=0\{\begin{array}{l}{x}_1=0\\ \frac{d{x}_1}{dt}=0\end{array}\{\begin{array}{l}{x}_2=0\\ \frac{d{x}_2}{dt}=0\end{array}\end{array}}$

Sea el sistema de dos partículas de masas m₁=2 y m₂=1, unidas por muelles de constantes k₁=6, k₂=3 y k₃=0. Los coeficientes de la fuerza de rozamiento λ₁=λ₂=c, λ₃=0, con c=1. Se aconseja cambiar el valor de c y ver el efecto sobre el estado transitorio del oscilador. La frecuencia de la fuerza oscilante se ha establecido en ${\omega }_f={\omega }_1=\sqrt{\frac{3}{2}}$ . Se aconseja cambiar este valor.

Para utilizar la función ode45 de MATLAB es necesario transformar el sistema de dos ecuaciones diferenciales de segundo orden en cuatro de primer orden, denominando x₁=y₁, dx₁/dt=y₂, x₂=y₃ y dx₂/dt=y₄

${\displaystyle \{\begin{array}{l}\frac{d{y}_1}{dt}=y_2\\ \frac{d{y}_2}{dt}=-\frac{\left({\lambda }_1+{\lambda }_2\right)}{m_1}{y}_2+\frac{{\lambda }_2}{m_1}{y}_4-\frac{\left(k_1+k_2\right)}{m_1}{y}_1+\frac{k_2}{m_1}{y}_3+\frac{F_1(t)}{m_1}\\ \frac{d{y}_3}{dt}=y_4\\ \frac{d{y}_4}{dt}=\frac{{\lambda }_2}{m_2}{y}_2-\frac{\left({\lambda }_2+{\lambda }_3\right)}{m_2}{y}_4+\frac{k_2}{m_2}{y}_1-\frac{\left(k_2+k_3\right)}{m_2}{y}_3+\frac{F_2(t)}{m_2}\end{array}}$

En el script resolvemos el sistema de dos ecuaciones diferenciales de segundo orden, mediante la función ode45 de MATLAB

function acoplados_3
    y0=[0,0,0,0]; %condiciones iniciales
    tspan=[0,30];
    [t,y]=ode45(@modoamortiguada,tspan,y0);

    hold on
    plot(t,y(:,1),'b')
    plot(t,y(:,3),'r')
    hold off
    grid on
    xlabel('t')
    ylabel('x1,x2');
    title('osciladores acoplados, forzados')

    function f=modoamortiguada(t,y)
        m1=2;
        m2=1;
        k1=6;
        k2=3;
        k3=0;

        c=1;  %coeficiente de la fuerza de rozamiento
        c1=c;
        c2=c;
        c3=0;

        wf=sqrt(3/2); %frecuencia de la fuerza oscilante
        F2=2*cos(wf*t);
        F1=0;

        f=[y(2);(-(c1+c2)*y(2)+c2*y(4)-(k1+k2)*y(1)+k2*y(3)+F1)/m1;...
            y(4);(-(c2+c3)*y(4)+c2*y(2)-(k3+k2)*y(3)+k2*y(1)+F2)/m2];
    end

end

Obtenemos una gráfica similar a la figura anterior, aunque la amplitud final en el estado estacionario difiere un poco del calculado de modo exacto.

Referencia

Lecture 21: MODAL ANALYSIS OF UNDAMPED FORCED MDOF SYSTEMS