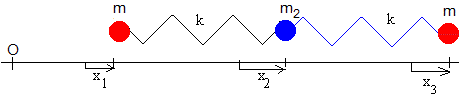
Sistema formado por tres partículas y dos muelles
Consideremos el sistema de la figura: tres partículas de masa m, m2 y m unidas por dos muelles de la misma constante k. En el instante t, la primera partícula se desplaza x1 de su posición de equilibrio, la segunda x2 y la tercera x3
La Lagrangiana de este sistema es
Las ecuaciones del movimiento de cada una de las tres partículas
En forma matricial
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles.
Valores propios
Buscamos una solución de la forma
x1=X1sin(ωt+φ), x2=X2sin(ωt+φ), x3=X3sin(ωt+φ)
que representan MAS de amplitud X1, X2, X3 y frecuencia angular ω.
Tenemos un sistema homogéneo, los cuadrados de las frecuencias ω2 de los modos normales de vibración se calculan haciendo que el determinante de los coeficientes sea igual a cero
El resultado es
>> syms k m m2; >> M=diag([m,m2,m]); >> K=[k,-k,0;-k,2*k,-k;0,-k,k]; >> [V,D]=eig(M^-1*K) V = %vectores propios [ 1, -1, 1] [ 1, 0, -(2*m)/m2] [ 1, 1, 1] D = %cuadrado de las frecuencias [ 0, 0, 0] [ 0, k/m, 0] [ 0, 0, (2*k*m + k*m2)/(m*m2)]
Vectores propios
Dado el valor de X1=1, calculamos X2 y X3 tomando dos ecuaciones del sistema homogéneo de tres ecuaciones con tres incógnitas, para cada una de las frecuencias de los modos normales de vibración
Vamos a dividir los vectores X(1), X(2) y X(3) por un factor de escala de modo que
Como X es un vector columna, XT es vector fila
>> X1=V(:,1); >> r=X1'*M*X1 r =2*m + m2 >> X1=X1/sqrt(r); >> r=X2'*M*X2 r =2*m >> X2=V(:,2); >> X2=X2/sqrt(r); >> X3=V(:,3); >> r=X3'*M*X3 r =2*m + (4*m*conj(m))/conj(m2)
Math Symbolic de MATLAB no calcula adecuadamente estas operaciones con vectores y matrices
Superposición
Como vimos en la página anterior, el desplazamiento xi(t) de cada una de las partículas es combinación la lineal
En forma matricial escribimos
El vector V tiene por columnas los vectores X(1), X(2) y X(3)
Ecuaciones del movimiento desacopladas
Las nuevas ecuaciones del movimiento expresadas en términos de las coordenadas u(t) están desacopladas y sus soluciones son conocidas: movimiento rectilíneo uniforme para ω1=0, y Movimiento Armónico Simple para ω2 y ω3. Las soluciones de estas ecuaciones diferenciales son:
donde las constantes Ai y Bi se determinan a partir de las condiciones iniciales
Condiciones iniciales
Las condiciones inicales vienen determinadas por el desplazamiento y velocidad de cada una de las partículas en el instante t=0. Todas las partículas parten de su posición inicial en equilibrio en reposo, salvo la primera partícula a la que se le proporciona una velocidad inicial p/m siendo p el momento lineal.
Las condiciones iniciales en el espacio u se escriben en forma matricial
Como x(0)=0 entonces u(0)=0, por lo que B1=0, A2=0, A3=0
Las ecuaciones del movimiento en el espacio u(t) son
Finalmente, el desplazamiento de cada una de las partículas respecto del tiempo, el vector x se obtiene, multiplicando la matriz V por el vector u
El resultado final es
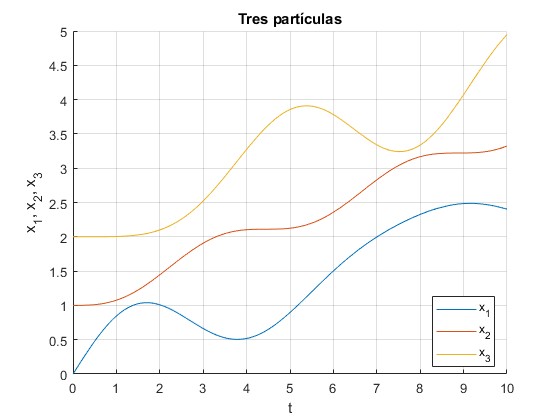
Representamos el desplazamiento de cada una de las tres partículas x1(t), x2(t) y x3(t) para el siguiente sistema:
- Constante de los dos muelles, k=1
- Masa de las partículas situadas en los extremos, m=1
- Masa de la partícula situada en el centro, m2=2
- Momento lineal inicial de la primera partícula, p=1
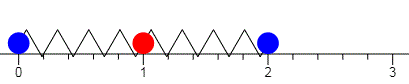
Situación inicial de las partículas en el instante t=0
k=1; %constante de los dos muelles
m=1; %masas de las partículas de los extremos
m2=2; %masa de la particula del centro
p=1; %momento lineal (primera partícula)
M=diag([m,m2,m]); %matriz masas
K=[k,-k,0;-k,2*k,-k;0,-k,k]; %matriz constante
[V,D]=eig(M^-1*K);
w=diag(sqrt(D)); %vector de frecuencias propias
w=fliplr(w');
disp(w)
x1=@(t) p*(t/(2*m+m2)+sin(w(2)*t)/(2*m*w(2))+m2*sin(w(3)*t)/(2*m*(m2+2*m)*w(3)));
x2=@(t) 1+p*(t/(2*m+m2)-sin(w(3)*t)/((m2+2*m)*w(3)));
x3=@(t) 2+p*(t/(2*m+m2)-sin(w(2)*t)/(2*m*w(2))+m2*sin(w(3)*t)/(2*m*(m2+2*m)*w(3)));
hold on
fplot(x1,[0,10])
fplot(x2,[0,10])
fplot(x3,[0,10])
hold off
xlabel('t')
legend('x_1', 'x_2', 'x_3', 'location', 'best')
ylabel('x_1, x_2, x_3')
grid on
title('Tres partículas')
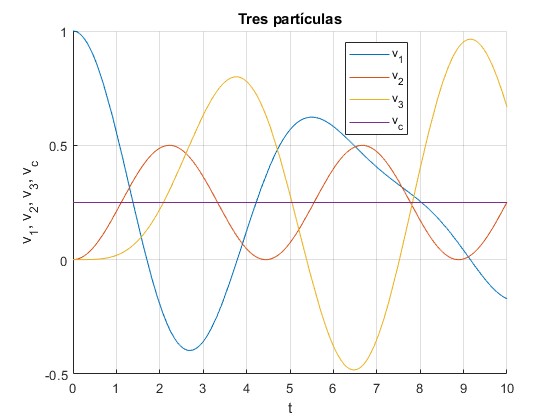
Derivando respecto del tiempo, obtenemos las velocidades de las partículas
Comprobamos que la velocidad del centro de masas es constante
Con los valores de los parámetros de este sistema, vcm=1/4=0.25
k=1; %constante de los dos muelles
m=1; %masas de las partículas de los extremos
m2=2; %masa de la particula del centro
p=1; %momento lineal (primera partícula)
M=diag([m,m2,m]); %matriz masas
K=[k,-k,0;-k,2*k,-k;0,-k,k]; %matriz constante
[V,D]=eig(M^-1*K);
w=diag(sqrt(D)); %vector de frecuencias propias
w=fliplr(w');
v1=@(t) p*(1/(2*m+m2)+cos(w(2)*t)/(2*m)+m2*cos(w(3)*t)/(2*m*(m2+2*m)));
v2=@(t) p*(1/(2*m+m2)-cos(w(3)*t)/((m2+2*m)));
v3=@(t) p*(1/(2*m+m2)-cos(w(2)*t)/(2*m)+m2*cos(w(3)*t)/(2*m*(m2+2*m)));
vCM=@(t) (m*v1(t)+m*v3(t)+m2*v2(t))/(2*m+m2);
hold on
fplot(v1,[0,10])
fplot(v2,[0,10])
fplot(v3,[0,10])
fplot(vCM,[0,10])
hold off
xlabel('t')
legend('v_1', 'v_2', 'v_3', 'v_c', 'location', 'best')
ylabel('v_1, v_2, v_3, v_c')
grid on
title('Tres partículas')
Actividades
Observamos el movimiento de las tres partículas del sistema con los siguientes datos:
- Constante de los dos muelles, k=1
- Masa de las partículas situadas en los extremos, m=1
- Masa de la partícula situada en el centro, m2, se puede modificar en el control titulado Masa partícula roja
- Momento lineal inicial de la primera partícula, p=0.5, se puede modificar en el control titulado Momento lineal
La situación inicial de las partículas en el instante t=0 es x01=0, x02=1, x03=2
Referencias
Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 2032, pp. 529-532

