Modos normales de vibración (I)

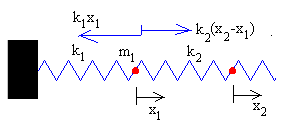
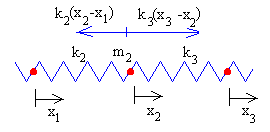
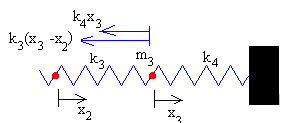
Supongamos que la primera partícula se desplaza x1 de la posición de equilibrio, que la segunda se desplaza x2 y la tercera, se desplaza x3.
En las figuras, se muestra las fuerzas sobre cada una de las partículas
Ecuación del movimiento de la primera partícula
Ecuación del movimiento de la segunda partícula
Ecuación del movimiento de la tercera partícula
En forma matricial
En general, tendremos para n partículas unidas a n+1 muelles
Los modos normales de vibración y sus propiedades
Supongamos un sistema formado por tres partículas de la misma masa m unidas por muelles elásticos iguales de constante k, tal como se muestra en la figura. Este ejemplo, nos va a servir para elaborar un script que nos permita estudiar cualquier configuración de muelles y partículas.

En este caso, las tres ecuaciones diferenciales del movimiento se escriben
En forma matricial
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles. Fijamos el valor de la masa m=1 y de la constante k=1 de los muelles.
Valores y vectores propios
Buscamos una solución de la forma
x1=X1sin(ωt+φ1), x2=X2sin(ωt+φ2), x3=X3sin(ωt+φ3)
que representan MAS de amplitud X1, X2, X3 , frecuencia angular ω.
Las frecuencias de los modos normales de vibración se calculan resolviendo el sistema homogéneo
;
Como la matriz M es diagonal su inversa M-1 es tambien diagonal
>> K=sym('[2,-1,0;-1,2,-1;0,-1,2]');
>> [V,D]=eig(K)
V =
[ 1, 1, -1]
[ 2^(1/2), -2^(1/2), 0]
[ 1, 1, 1]
D =
[ 2 - 2^(1/2), 0, 0]
[ 0, 2^(1/2) + 2, 0]
[ 0, 0, 2]
Los cuadrados de las frecuencias de los modos normales de vibración están en la diagonal de la matriz D. El vector propio correspondiente a cada uno de los valores propios son los vectores columna X(1), X(2) y X(3) de la matriz V, tal como se indica a continuación:
Propiedades de los vectores propios
Comprobamos las siguientes propiedades de los vectores propios X(1), X(2) y X(3)
donde el símbolo T indica traspuesta (cambiar filas por columnas)
>> X1=V(:,1); >> X2=V(:,2); >> X3=V(:,3); >> r=X1'*K*X2 r =4 - 2^(1/2)*(2*2^(1/2) - 2) - 2*2^(1/2) >> simplify(r) ans =0 >> r=X3'*K*X1 r =0 >> r=X2'*K*X3 r =0 >> r=X2'*M*X1 r =0 >> r=X3'*M*X2 r =0 >> r=X1'*M*X1 r =4 >> r=X2'*M*X2 r =4 >> r=X3'*M*X3 r =2 >> r=X1'*K*X1 r =8 - 4*2^(1/2) >> r=X2'*K*X2 r =4*2^(1/2) + 8 >> r=X3'*K*X3 r =4
El cociente
es el cuadrado de las frecuencias de cada uno de los modos normales de vibración
Vamos a dividir los vectores X(1), X(2) y X(3) por un factor de escala de modo que
De este modo, los cuadrados de las frecuencias de cada cada uno de los modos normales de vibración se calcularán a partir de la matriz K de las constantes de los muelles.
Como
Al vector X(1) tendremos que dividirlo entre dos, X(2) habrá que dividirlo entre dos y a X(3)entre raíz de dos
>> X1=X1/2;
>> X2=X2/2;
>> X3=X3/sym('sqrt(2)');
>> X1'*M*X1
ans =1
>> X2'*M*X2
ans =1
>> X3'*M*X3
ans =1
>> X1'*K*X1
ans =2 - 2^(1/2)
>> X2'*K*X2
ans =2^(1/2) + 2
>> X3'*K*X3
ans =2
Los nuevos vectores X(1), X(2) y X(3)son
y la nueva matriz V, formada por los vectores columna X(1), X(2) y X(3) es
Comprobamos que
donde Mg y Kg la nueva matriz de masas y la nueva matriz diagonal de las constantes de los muelles. En la diagonal de esta matriz aparecen los cuadrados de las frecuencias de los modos normales de vibración
>> V=[X1,X2,X3] V = [ 1/2, 1/2, -2^(1/2)/2] [ 2^(1/2)/2, -2^(1/2)/2, 0] [ 1/2, 1/2, 2^(1/2)/2] >> V'*M*V ans = [ 1, 0, 0] [ 0, 1, 0] [ 0, 0, 1] >> V'*K*V ans = [ 2 - 2^(1/2), 0, 0] [ 0, 2^(1/2) + 2, 0] [ 0, 0, 2]
Superposición
Como vimos en la página anterior, el desplazamiento xi(t) de cada una de las partículas es combinación la lineal
En forma matricial escribimos
Ecuaciones del movimiento desacopladas
En la ecuación diferencial del movimiento reemplazamos
y multiplicamos por la matriz traspuesta de V.
Las nuevas ecuaciones del movimiento expresadas en términos de las coordenadas u(t) están desacopladas y su solución es bien conocida, un Movimiento Armónico Simple. Las soluciones de estas ecuaciones diferenciales son:
donde las constantes Ai y Bi se determinan a partir de las condiciones iniciales
Condiciones iniciales
Las condiciones inicales vienes determinadas por el desplazamiento de la posición de equilibrio y velocidad de cada una de las partículas en el instante t=0. Por ejemplo, desplazamos las partículas de sus posición de equilibrio y las soltamos
Teniendo en cuenta la relación entre xi(t) y ui(t)
En vez de calcular la matriz inversa de V, la sustituimos por un producto de matrices, que es más conveniente
Las nuevas condiciones iniciales se escriben en forma matricial
Como ejemplo tomemos las condiciones iniciales siguientes
>> x0=[1;0;0]; %posición
>> xp0=[0;0;0]; %velocidad (x prima)
>> u0=V'*M*x0 %posición transformada
u0 =
1/2
1/2
-2^(1/2)/2
>> up0=V'*M*xp0 %velocidad (u prima) transformada
up0 =
0
0
0
A partir de las condiciones iniciales en el espacio u
determinamos las constantes Ai y Bi
Finalmente, la posición de cada una de las partículas respecto del tiempo, el vector x se obtiene, multiplicando la matriz cuadrada V por el vector u
>> syms t;
>> u1=cos(sqrt(D(1,1))*t)/2;
>> u2=cos(sqrt(D(2,2))*t)/2;
>> u3=-cos(sqrt(D(3,3))*t)*sqrt(2)/2;
>> u=[u1;u2;u3];
>> x=V*u
cos(t*(2^(1/2) + 2)^(1/2))/4 + cos(2^(1/2)*t)/2 +
cos(t*(2 - 2^(1/2))^(1/2))/4
-(2^(1/2)*(cos(t*(2^(1/2) + 2)^(1/2)) -
cos(t*(2 - 2^(1/2))^(1/2))))/4
cos(t*(2^(1/2) + 2)^(1/2))/4 - cos(2^(1/2)*t)/2 +
cos(t*(2 - 2^(1/2))^(1/2))/4
>> hold on
>> ezplot(x(1),[0 20])
>> g=ezplot(x(2),[0 20]);
>> set(g,'color','red')
>> g=ezplot(x(3),[0 20]);
>> set(g,'color','green')
>> grid on
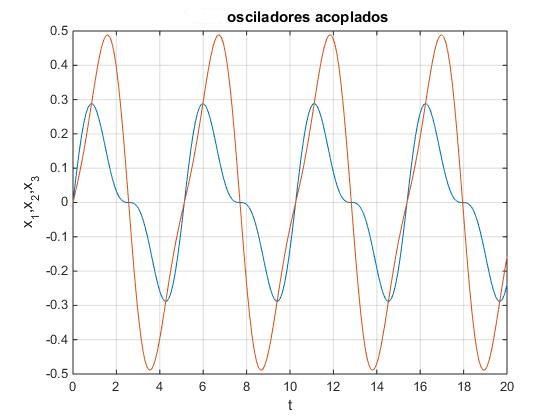
Representación gráfica del movimiento de cada partícula
Solamente nos queda unir las distintas porciones de código MATLAB en un script que nos permita resolver el sistema formado por tres partículas y optimizar el código para que pueda ser generalizable a cualquier configuración
syms t;
%matriz de las constantes de los muelles
K=sym('[2,-1,0;-1,2,-1;0,-1,2]');
M=sym('[1,0,0;0,1,0;0,0,1]'); %matriz de las masas
[V,D]=eig(inv(M)*K); %valores y vectores propios
w=diag(sqrt(D)); %vector de frecuencias propias
for i=1:length(w) %para hacer diagonal K
r=V(:,i)'*M*V(:,i);
V(:,i)=V(:,i)/sqrt(r);
end
%condiciones iniciales
x0=sym('[1;0;0]'); %posición inicial
xp0=sym('[0;0;0]'); %velocidad (x prima) inicial
u0=V'*M*x0;
up0=V'*M*xp0;
%movimiento de cada una de las partículas
A=u0;
B=up0./diag(D);
u=diag(A)*cos(w*t)+diag(B)*sin(w*t);
x=V*u;
x=simplify(x)
%representación gráfica
color=['b','r','g'];
hold on
for i=1:length(w)
h=ezplot(x(i),[0,20]);
set(h,'color',color(i))
end
title('Tres osciladores acoplados')
ylabel('x_1,x_2,x_3')
xlabel('t')
grid on
hold off
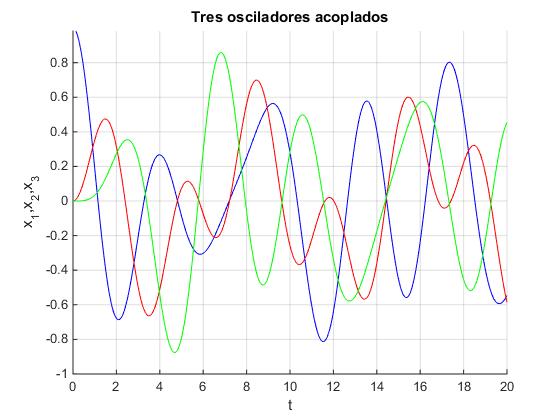
En la ventana de comandos obtenemos las frecuencias de los modos normales de vibración y el vector x(t), posición de cada partícula en función del tiempo, cuya representación gráfica se muestra en la figura: la primera en color azul, la segunda en color rojo y la tercera en color verde..
w =
(2 - 2^(1/2))^(1/2)
(2^(1/2) + 2)^(1/2)
2^(1/2)
x = cos(t*(2^(1/2) + 2)^(1/2))/4 + cos(2^(1/2)*t)/2
+ cos(t*(2 - 2^(1/2))^(1/2))/4
-(2^(1/2)*(cos(t*(2^(1/2) + 2)^(1/2)) -
cos(t*(2 - 2^(1/2))^(1/2))))/4
cos(t*(2^(1/2) + 2)^(1/2))/4 - cos(2^(1/2)*t)/2
+ cos(t*(2 - 2^(1/2))^(1/2))/4
Cambiamos la matriz K de las constantes de los muelles elásticos, la matriz M de las masas y los vectores posición inicial x0 y velocidad inicial xp0. Si se incrementa la dimensión de la matrices hay que añadir más colores al vector
El siguiente script es similar al anterior pero que funciona con la versión básica de MATLAB mientras que en el anterior es necesario disponer del complemento Math Symbolic por lo que se aconseja su utilización, salvo en aquellos casos en los que sea preciso obtener una respuesta analítica exacta.
K=[2,-1,0;-1,2,-1;0,-1,2]; %matriz constante de los muelles
M=[1,0,0;0,1,0;0,0,1]; %matriz de las masas
[V,D]=eig(inv(M)*K); %valores y vectores propios
w=diag(sqrt(D)) %vector de frecuencias propias
for i=1:length(w)
r=V(:,i)'*M*V(:,i);
V(:,i)=V(:,i)/sqrt(r);
end
%condiciones iniciales
x0=[1;0;0]; %posición inicial
xp0=[0;0;0]; %velocidad (x prima) inicial
u0=V'*M*x0;
up0=V'*M*xp0;
%movimiento de cada una de las partículas
A=u0;
B=up0./diag(D);
t=linspace(0,20,200);
u=diag(A)*cos(w*t)+diag(B)*sin(w*t);
x=V*u;
%representación gráfica
plot(t,x);
title('Tres osciladores acoplados')
ylabel('x_1,x_2,x_3')
xlabel('t')
grid on
Obtenemos una gráfica similar, pero los colores de las representación gráfica de la posición xi(t) de cada partícula lo establece MATLAB.
En la ventana de comandos obtenemos las frecuencias de los modos normales de vibración
w =
0.7654
1.4142
1.8478
Frecuencias de los modos normales de vibración
Sistema formado por dos partículas
Las ecuaciones del movimiento son
expresadas en forma matricial
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz M-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k m;
>> M=[m,0;0,m];
>> K=[2*k,-k;-k,2*k];
>> [V,D]=eig(M^-1*K);
>> w2 =diag(D)
w2 =
k/m
(3*k)/m
>> V
V =
[ 1, -1]
[ 1, 1]
| Valores propios ω2 | Vectores propios |
(1, 1) |
|
(-1,1) |
Sistema formado por tres partículas

Las ecuaciones del movimiento son
expresada en forma matricial
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz M-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k m;
>> M=[m,0,0;0,m,0; 0,0,m];
>> K=[2*k,-k,0;-k,2*k,-k;0,-k,2*k];
>> [V,D]=eig(M^-1*K);
>> w2 =diag(D)
w2 =
(k*(2^(1/2) + 2))/m
-(k*(2^(1/2) - 2))/m
(2*k)/m
>> V
V =
[ 1, 1, -1]
[ -2^(1/2), 2^(1/2), 0]
[ 1, 1, 1]
| Valores propios ω2 | Vectores propios |
|
|
|
|
(-1,0,1) |
Sistema formado por cuatro partículas

Las ecuaciones del movimiento son
expresadas en forma matricial
La primera es la matriz M de las masas y la segunda es la matriz K de las constantes de los muelles. Las frecuencias de los modos normales de vibración ω2 son los valores propios de la matriz M-1K. El vector propio correspondiente a cada uno de los valores propios son los vectores columna de la matriz V
>> syms k m; >> M=[m,0,0,0;0,m,0,0; 0,0,m,0; 0,0,0,m]; >> K=[2*k,-k,0,0;-k,2*k,-k,0;0,-k,2*k,-k;0,0,-k,2*k]; >> [V,D]=eig(M^-1*K); >> w2 =diag(D) w2 = (k*(5^(1/2) + 3))/(2*m) -(k*(5^(1/2) - 3))/(2*m) (k*(5^(1/2) + 5))/(2*m) -(k*(5^(1/2) - 5))/(2*m) >> V V = [ 1, 1, -1, -1] [ 1/2 - 5^(1/2)/2, 5^(1/2)/2 + 1/2, 5^(1/2)/2 + 1/2, 1/2 - 5^(1/2)/2] [ 1/2 - 5^(1/2)/2, 5^(1/2)/2 + 1/2, - 5^(1/2)/2 - 1/2, 5^(1/2)/2 - 1/2] [ 1, 1, 1, 1]
| Valores propios ω2 | Vectores propios |
|
|
|
|
|
|
|
Actividades
Se ha fijado
- La masa de las partículas, m=1 kg
- La constante elástica de los muelles, k=1 N/m
Se introduce
-
El número N de partículas, en el control titulado Partículas
Se pulsa el botón titulado Nuevo
Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular.
Se pulsa el botón titulado >>, observamos los siguientes modos normales
Se pulsa el botón titulado << para observar el modo normal de vibración anterior.
En la parte inferior, se muestra el desplazamiento de las partículas
Ejemplos
Probamos con los ejemplos estudiados en la página "Modos normales de vibración":
Ejemplo 1
El sistema está formado por dos partículas de masa m=1. La constante de los muelles es k1,3=10 y la constante del acoplamiento k2=0.5. Se desvía la primera partícula x01=1 de la posición de eqilibrio y se suelta. La posición inicial de la segunda partícula x02=0, velocidad inicial de ambas v01=0, v02=0.
k1=10; k2=0.5; k3=10; m1=1; m2=1; K=[(k1+k2),-k2;-k2,(k2+k3)]; %sistema de dos partículas M=[m1,0;0,m2]; .... %condiciones iniciales x0=[1;0]; xp0=[0;0]; ....
En la ventana de comandos obtenemos las frecuencias de los modos normales de vibración
w =
3.1623
3.3166
Utilizamos alternativamente, el script de cálculo simbólico
syms k1 k2 k3 m1 m2;
K=[(k1+k2),-k2;-k2,(k2+k3)];
M=[m1,0;0,m2];
K=subs(K,{k1,k2,k3},{10,0.5,10});
M=subs(M,{m1,m2},{1,1});
....
%condiciones iniciales
x0=sym('[1;0]');
xp0=sym('[0;0]');
.....
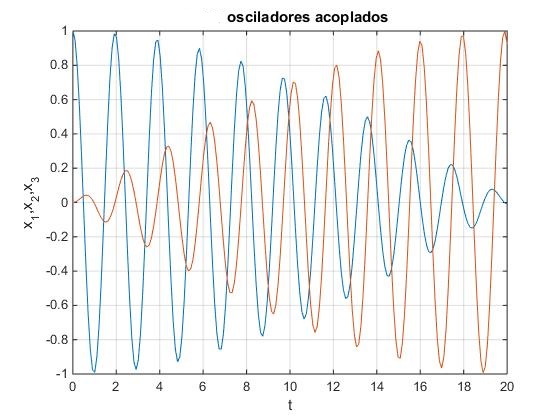
En la ventana de comandos obtenemos la expresión de las posiciones de las partículas en función del tiempo, x1(t) y x2(t). Los argumentos de las funciones coseno son las frecuencias de los modos normales de vibración
x = cos(10^(1/2)*t)/2 + cos(11^(1/2)*t)/2 cos(10^(1/2)*t)/2 - cos(11^(1/2)*t)/2
Ejemplo 2
El sistema formado por dos partículas de masas m1=10 y m2=1 unidas por muelles de constantes k1=30, k2=5 y k3=0. Las condiciones iniciales en el instante t=0, son las siguientes: posición inicial x01=1, x02=0, velocidad inicial v01=0, v02=0.
k1=30; k2=5; k3=0;m1=10; m2=1; K=[(k1+k2),-k2;-k2,(k2+k3)]; M=[m1,0;0,m2]; .... %condiciones iniciales x0=[1;0]; xp0=[0;0]; ...
En la ventana de comandos obtenemos las frecuencias de los modos normales de vibración
w =
1.5811
2.4495
Utilizamos alternativamente, el script de cálculo simbólico
syms k1 k2 k3 m1 m2;
K=[(k1+k2),-k2;-k2,(k2+k3)]; %para un sistema de dos partículas
M=[m1,0;0,m2];
K=subs(K,{k1,k2,k3},{30,5,0});
M=subs(M,{m1,m2},{10,1});
....
%condiciones iniciales
x0=sym('[1;0]');
xp0=sym('[0;0]');
.....
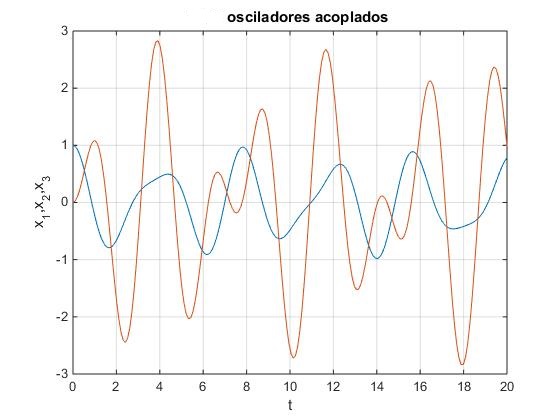
En la ventana de comandos obtenemos la expresión de las posiciones de las partículas en función del tiempo, x1(t) y x2(t). Los argumentos de las funciones coseno son las frecuencias de los modos normales de vibración
X = (2*cos(6^(1/2)*t))/7 + (5*cos((10^(1/2)*t)/2))/7 (10*cos((10^(1/2)*t)/2))/7 - (10*cos(6^(1/2)*t))/7
Ejemplo 3
El sistema formado por dos partículas de masas m1=2 y m2=1 unidas por muelles de constantes k1=6, k2=3 y k3=0. Las condiciones iniciales en el instante t=0, son las siguientes: posición inicial x01=0, x02=0, velocidad inicial v01=1, v02=0.
En la ventana de comandos obtenemos las frecuencias de los modos normales de vibración
w =
2.4495
1.2247

