Sistema no aislado de dos partículas interactuantes

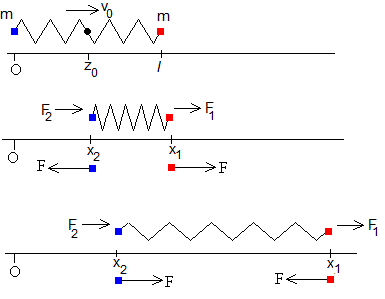
Consideremos un sistema de dos partículas cada una de masa m, unidas por un muelle elástico o una goma elástica de constante k y de longitud l si deformar.

Se aplica una fuerza externa F₁ y F₂ sobre cada una de las partículas. Estas fuerzas dependen de la posición de cada una de ellas, x₁ y x₂.

En la figura se muestra:

en la parte superior, la situación inicial cuando el muelle de longitud l está sin deformar. El centro de masas está situado en la posición z₀ y se mueve con velocidad v₀
en la parte intermedia, cuando el muelle está comprimido. Como (x₁-x₂) es menor que l, la fuerza de interacción F es positiva para la partícula de la derecha y es negativa para la partícula de la izquierda.
en la parte inferior, cuando el muelle está estirado. Como (x₁-x₂) es mayor que l, la fuerza F es negativa para la partícula de la derecha y es positiva para la partícula de la izquierda .

Ecuaciones del movimiento

Las ecuaciones del movimiento para cada una de las dos partículas son,

$\begin{array}{l} m \frac{d^{2} x_{1}}{d t^{2}} = F_{1} + k (l - (x_{1} - x_{2})) \\ m \frac{d^{2} x_{2}}{d t^{2}} = F_{2} - k (l - (x_{1} - x_{2})) \end{array}$

Movimiento del centro de masa

Si sumamos las dos ecuaciones tenemos

$\begin{array}{l} \frac{d^{2} (x_{1} + x_{2})}{d t^{2}} = \frac{F_{1} + F_{2}}{m} \\ \frac{d^{2} z}{d t^{2}} = \frac{F_{1} + F_{2}}{2 m} \end{array}$

donde z=(mx₁+mx₂)/(m+m)=(x₁+x₂)/2, es la posición del centro de masas

Movimiento relativo de las dos partículas

$\begin{array}{l} \frac{d^{2} (x_{1} - x_{2})}{d t^{2}} = \frac{F_{1} - F_{2}}{m} + 2 \frac{k}{m} (l - (x_{1} - x_{2})) \\ \frac{d^{2} ξ}{d t^{2}} = \frac{F_{1} - F_{2}}{2 m} + \frac{k}{m} (l - 2 ξ) \end{array}$

donde ξ=(x₁-x₂)/2 es la posición relativa de las dos partículas.

Posición de cada una de las dos partículas

Conocida la posición z del centro de masas y la posición relativa ξ de las partículas en función del tiempo t, determinamos la posición de cada una de las partículas

$\begin{array}{l} {\begin{cases} x_{1} + x_{2} = 2 z \\ x_{1} - x_{2} = 2 ξ \end{cases} \\ x_{2} = z - ξ, x_{1} = z + ξ \end{array}$

Las fuerzas externas

Supongamos que F₁ y F₂ son dos fuerzas conservativas derivadas de la energía potencial E_p(x)

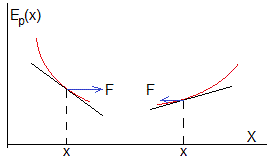
$F_{1} = {- \frac{d E_{p} (x)}{d x} |}_{x = x_{1}}, F_{2} = {- \frac{d E_{p} (x)}{d x} |}_{x = x_{2}}$

Sea E_p(x) la función

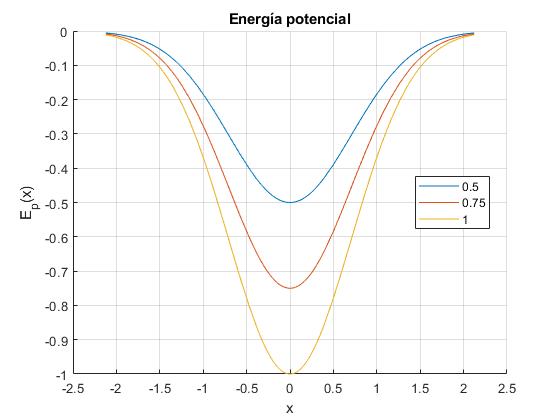
$\begin{array}{l} E_{p} (x) = - m g h \exp (- \frac{x^{2}}{2 a^{2}}) \\ F = - \frac{d E_{p} (x)}{d x} = - \frac{m g h}{a^{2}} x \exp (- \frac{x^{2}}{2 a^{2}}) \end{array}$

Tomamos la masa de las partículas como unidad m=1 kg y el parámetro a²=1/2. Representamos E_p(x) para los siguientes valores de gh=0.5, 0.75, 1

a=1/sqrt(2);
m=1;
hold on
for gh=[0.5,0.75,1]
    Ep=@(x) -m*gh*exp(-x.^2/(2*a^2));
    fplot(Ep,[-3*a,3*a],'displayName',num2str(gh))
 end
hold off
grid on
xlabel('x')
legend('-DynamicLegend','location','best')
ylabel('E_p(x)')
title('Energía potencial')

Sistema de dos ecuaciones diferenciales

Las ecuaciones del movimiento del centro de masas y del movimiento relativo se escriben en términos de z y ξ

Movimiento del centro de masas

$\begin{array}{l} \frac{d^{2} z}{d t^{2}} = \frac{F_{1} + F_{2}}{2 m} \\ \frac{d^{2} z}{d t^{2}} = - \frac{g h}{2 a^{2}} (x_{1} \exp (- \frac{x_{1}^{2}}{2 a^{2}}) + x_{2} \exp (- \frac{x_{2}^{2}}{2 a^{2}})) \\ \frac{d^{2} z}{d t^{2}} = - \frac{g h}{2 a^{2}} ((z + ξ) \exp (- \frac{{(z + ξ)}^{2}}{2 a^{2}}) + (z - ξ) \exp (- \frac{{(z - ξ)}^{2}}{2 a^{2}})) \end{array}$

Movimiento relativo

$\begin{array}{l} \frac{d^{2} ξ}{d t^{2}} = \frac{F_{1} - F_{2}}{2 m} + \frac{k}{m} (l - 2 ξ) \\ \frac{d^{2} ξ}{d t^{2}} = - \frac{g h}{2 a^{2}} (x_{1} \exp (- \frac{x_{1}^{2}}{2 a^{2}}) - x_{2} \exp (- \frac{x_{2}^{2}}{2 a^{2}})) + \frac{k}{m} (l - 2 ξ) \\ \frac{d^{2} ξ}{d t^{2}} = - \frac{g h}{2 a^{2}} ((z + ξ) \exp (- \frac{{(z + ξ)}^{2}}{2 a^{2}}) - (z - ξ) \exp (- \frac{{(z - ξ)}^{2}}{2 a^{2}})) + \frac{k}{m} (l - 2 ξ) \end{array}$

Se resuelve el sistema de dos ecuaciones diferenciales por procedimientos numéricos, con las siguientes condiciones iniciales

El centro de masa del sistema parte de la posición z₀, y el muelle está sin deformar, su longitud es l, ξ₀=l/2
La velocidad del centro de masa es v₀ y la velocidad inicial relativa es cero

${(\frac{d z}{d t})}_{t = 0} = v_{0}, {(\frac{d ξ}{d t})}_{t = 0} = 0$

Balance energético

Las fuerzas externas F₁ y F₂ son conservativas.

El trabajo de una fuerza conservativa es igual a la diferencia entre la energía potencial E_p(x) inicial en A y final en B.

$\begin{array}{l} W_{1} = \int_{A}^{B} F_{1} d x = E_{p} (x_{1 A}) - E_{p} (x_{1 B}) \\ W_{2} = \int_{A}^{B} F_{2} d x = E_{p} (x_{2 A}) - E_{p} (x_{2 B}) \\ W_{e x t} = W_{1} + W_{2} = (E_{p} (x_{1 A}) - E_{p} (x_{1 B})) + (E_{p} (x_{2 A}) - E_{p} (x_{2 B})) \\ W_{e x t} = (E_{p} (z_{0} + ξ_{0}) - E_{p} (z + ξ)) + (E_{p} (z_{0} - ξ_{0}) - E_{p} (z - ξ)) \end{array}$

La energía cinética de las dos partículas del sistema es

$\begin{array}{l} E_{k B} = \frac{1}{2} m {(\frac{d x_{1}}{d t})}^{2} + \frac{1}{2} m {(\frac{d x_{2}}{d t})}^{2} = \frac{1}{2} m {(\frac{d z}{d t} + \frac{d ξ}{d t})}^{2} + \frac{1}{2} m {(\frac{d z}{d t} - \frac{d ξ}{d t})}^{2} = m {{(\frac{d z}{d t})}^{2} + {(\frac{d ξ}{d t})}^{2}} \\ E_{k A} = m v_{0}^{2} \end{array}$

La energía potencial del muelle

En la situación inicial el muelle está sin deformar, su longitud es l

$\begin{array}{l} E_{e B} = \frac{1}{2} k {(l - 2 ξ)}^{2} \\ E_{e A} = 0 \end{array}$

El balance energético se escribe

$\begin{array}{l} W_{e x t} = (E_{k B} - E_{k A}) + (E_{e B} - E_{e A}) \\ (E_{p} (z_{0} + ξ_{0}) - E_{p} (z + ξ)) + (E_{p} (z_{0} - ξ_{0}) - E_{p} (z - ξ)) = m {{(\frac{d z}{d t})}^{2} + {(\frac{d ξ}{d t})}^{2}} - m v_{0}^{2} + \frac{1}{2} k {(l - 2 ξ)}^{2} \end{array}$

Ejemplos

Estudiamos un sistema formado por dos partículas unidas por un muelle elástico, sometido a fuerzas externas conservativas

La masa de cada una de las partículas, m=1 kg
Longitud del muelle elástico, sin deformar, l=0.2 m
Constante elástica del muelle, k= 1 N/m
Parámetro de la fuerza externa, gh=1
Posición inicial del centro de masas, z₀=-3 m
Velocidad inicial del centro de masas, v₀=0.1 m/s
Posición relativa inicial, ξ₀=l/2
Velocidad relativa inicial, es nula

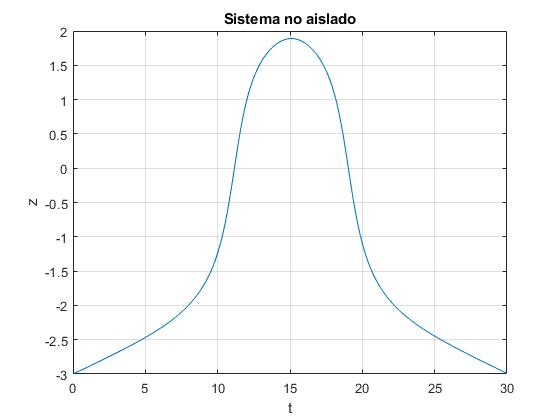
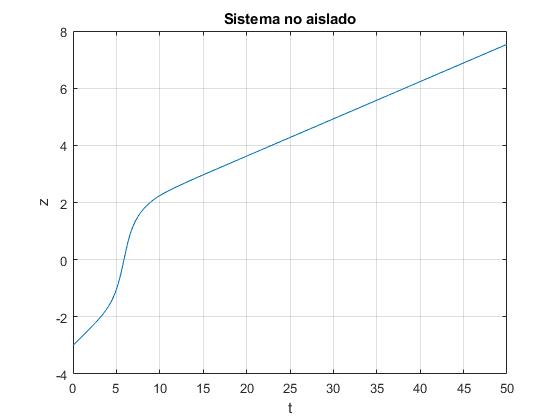
Representamos la posición z del centro de masas en función del tiempo t, resolviendo el sistema de dos ecuaciones difrenciales por el procedimiento ode45 de MATLAB

m=1; %masa de cada partícula
gh=1; %parámetro gh de la fuerza externa
k=1; % k/m, constante elástica
l=0.2; %longitud del muelle sin deformar
z0=-3; %posición inicial del centro de masas
v0=0.1; %velocidad inicial del centro de masas

fg=@(t,x)[x(2);-gh*((x(1)-x(3))*exp(-(x(1)-x(3))^2)+(x(1)+x(3))*
exp(-(x(1)+x(3))^2)); x(4); -gh*((x(1)+x(3))*exp(-(x(1)+x(3))^2)-
(x(1)-x(3))*exp(-(x(1)-x(3))^2))+k*(l-2*x(3))/m];
[t,x]=ode45(fg,[0,30],[z0,v0,l/2,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('z');
title('Sistema no aislado')

%balance energético
Ep=@(x) -m*gh*exp(-x.^2);
W_ext=Ep(x0+l/2)-Ep(x(end,1)+x(end,3))+Ep(x0-l/2)-Ep(x(end,1)-x(end,3));
Ek=m*(x(end,2)^2+x(end,4)^2)-m*v0^2;
Epot=k*(l-2*x(end,3))^2/2;
disp([W_ext,Ek+Epot])

Comprobamos el balance energético, el trabajo de las fuerzas externas es igual al la suma de las variaciones de energía cinética de las partículas y de la energía potencial del muelle deformado

   1.0e-03 *
    0.0206    0.3950

Representamos la velocidad del centro de masas dz/dt en función de la posición z, cambiando las líneas de código

....
plot(x(:,1),x(:,2))
grid on
xlabel('z')
ylabel('dz/dt');
title('Sistema no aislado')

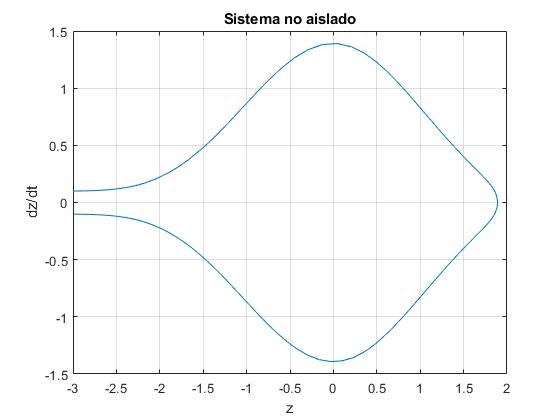
El sistema de dos partículas regresa al punto de partida, es reflejado por el pozo de potencial

Representamos la posición relativa ξ de las partículas en función del tiempo t, cambiando las líneas de código

...
plot(t,x(:,3))
grid on
xlabel('t')
ylabel('\xi');
title('Sistema no aislado')

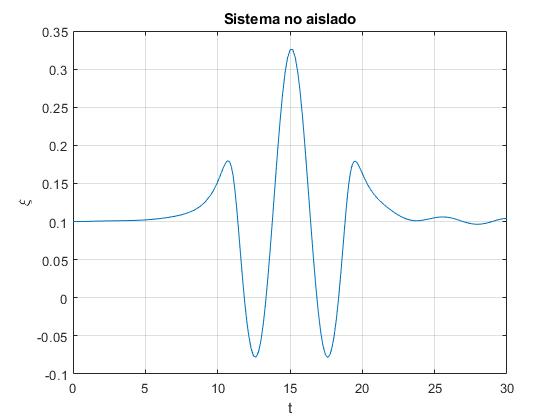
Repetimos las mismas representaciones con la velocidad inicial v₀=0.3 del centro de masas, comprobado que el sistema de dos partículas atraviesa el pozo de potencial, es transmitido

Actividades

Se introduce

La velocidad inicial v₀ del centro de masa, en el control titulado Velocidad inicial
La constante k del muelle elástico, en el control titulado Cte. muelle.
La profundidad gh del pozo de potencial, en el control titulado Profundidad
La posición inicial del centro de masas de las dos partículas es z₀=-3
La longitud del muelle sin deformar se ha fijado en l=0.7 m

Se pulsa el botón titulado Nuevo.

Se representa el pozo de potencial, y en la parte superior, las dos partículas (roja y azul) unidas por una goma elástica de color negro.

En la parte inferior izquierda se proporcionan los datos de

El tiempo t en s.
La posición x₁ de la partícula de color rojo
La posición x₂ de la partícula de color azul

En la parte inferior derecha se proporcionan los datos de

El trabajo W_ext de las fuerzas externas F₁ y F₂.
La energía potencial Ee del muelle deformado
La variación de energía cinética Ek de las dos partículas

Comprobamos que en cualquier instante, la suma de los dos últimos términos da el primero

Las flechas de color rojo, representan las fuerzas externas F₁ y F₂. Las de color azul, la fuerza F=k(l-2ξ) que ejerce el muelle sobre las partículas (iguales y de sentido contrario)

Velocidad inicial (m/s)
Cte. muelle (N/m)
Profundidad, g·h

Referencias

Mark Denny. Reflection from a Potential Well and from a Potential Barrier. The Physics Teacher. Vol. 60, May 2022, pp. 348-350