La plataforma y la partícula unida al muelle elástico constituyen un sistema aislado. Supongamos que inicialmente la partícula se encuentra en la posición de equilibrio, en reposo, encima del centro de masas del la plataforma. Su proyección sobre el eje horizontal X señala el origen O. Así pues, el origen O es la posición del centro de masas del sistema aislado que permanecerá en reposo si inicialmente lo estaba.

Posición

Supongamos que la partícula se desplaza de la posición de equilibrio s hacia la derecha. la plataforma se desplazará hacia la izquierda, su posición será x.

• La posición del centro de masa de la plataforma de masa M es x.
• La posición de la partícula de masa m es s+x.
• La posición del centro de masas del sistema aislado es el origen O

${\displaystyle 0=\frac{m(s+x)+Mx}{m+M}x=-\frac{m}{m+M}s}$

Velocidad

La velocidad de la plataforma es

${\displaystyle \frac{dx}{dt}=-\frac{m}{m+M}\frac{ds}{dt}}$

siendo ds/dt la velocidad relativa de la partícula respecto de la plataforma.

La velocidad de la partícula es

${\displaystyle \frac{dx}{dt}+\frac{ds}{dt}=\frac{M}{m+M}\frac{ds}{dt}}$

Aceleración

La aceleración de la plataforma es

${\displaystyle \frac{d^{2}x}{d{t}^2}=-\frac{m}{m+M}\frac{d^{2}s}{d{t}^2}}$

siendo d²s/dt² la aceleración relativa de la partícula respecto de la plataforma.

La aceleración de la partícula es

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{d^{2}s}{d{t}^2}=\frac{M}{m+M}\frac{d^{2}s}{d{t}^2}}$

Ecuaciones del movimiento

Aplicamos la segunda ley del Newton para obtener las ecuaciones del movimiento del bloque y de la plataforma

Ecuación del movimiento de la partícula

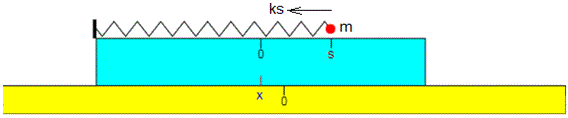
Sobre la partícula actúa la fuerza que ejerce el muelle deformado -ks.

${\displaystyle \begin{array}{l}m\left(\frac{M}{m+M}\frac{d^{2}s}{d{t}^2}\right)=-ks\\ \frac{d^{2}s}{d{t}^2}+\frac{k(m+M)}{mM}s=0\end{array}}$

Se trata de la ecuación diferencial de un Movimiento Armónico Simple

${\displaystyle s=A\sin \left(\omega t+\phi \right)\omega =\sqrt{\frac{k(m+M)}{mM}}}$

La velocidad relativa de la partícula respecto de la plataforma es

${\displaystyle \frac{ds}{dt}=A\omega \cos \left(\omega t+\phi \right)}$

La amplitud A y la fase inicial φ se determinan a partir de las condiciones iniciales: en el instante t=0, se estira el muelle s₀ y se suelta, ds/dt=0.

${\displaystyle t=0\left\{\begin{array}{l}{s}_0=A\sin \phi \\ 0=A\omega \cos \phi \end{array}\right\}\phi =\frac{\pi }{2}A=s_0}$

La ecuación del movimiento de la partícula sobre la plataforma es

${\displaystyle s=s_0\sin \left(\omega t+\frac{\pi }{2}\right)=s_0\cos \left(\omega t\right)}$

La posición de la partícula respecto del sistema de referencia inercial es

${\displaystyle s+x=\frac{M}{m+M}{s}_0\cos \left(\omega t\right)}$

La velocidad de la partícula respecto del sistema de referencia inercial es

${\displaystyle \frac{dx}{dt}+\frac{ds}{dt}=-\frac{M}{m+M}{s}_0\omega \sin \left(\omega t\right)}$

Ecuación del movimiento de la plataforma

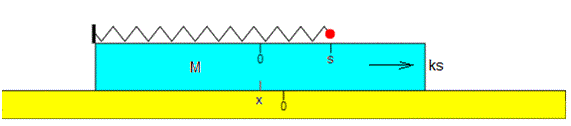
La plataforma de masa M experimenta una fuerza ks igual y de sentido contrario. La segunda ley de Newton se escribe para esta cuerpo

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=ks\\ M\frac{d^{2}x}{d{t}^2}=k\left(-\frac{m+M}{m}x\right)\\ \frac{d^{2}x}{d{t}^2}+k\frac{m+M}{mM}x=0\end{array}}$

La ecuación diferencial de un Movimiento Armónico Simple de la misma frecuencia, con las siguientes condiciones iniciales: en el instante t=0, la posición inicial de la plataforma es $-\frac{m}{m+M}{s}_0$ y su velocidad inicial es dx/dt=0

La posición de la plataforma es

${\displaystyle x=-\frac{m}{m+M}{s}_0\cos \left(\omega t\right)}$

Su velocidad es

${\displaystyle \frac{dx}{dt}=\frac{m}{m+M}{s}_0\omega \sin \left(\omega t\right)}$

Energías

La energía potencial elástica del muelle deformado s es

${\displaystyle \frac{1}{2}k{s}^2=\frac{1}{2}k{s}_0^2{\cos }^2\left(\omega t\right)}$

La energía cinética de la plataforma es

${\displaystyle \frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2=\frac{1}{2}M{\left(\frac{m}{m+M}\right)}^2{s}_0^2{\omega }^2{\sin }^2\left(\omega t\right)}$

La energía cinética de la partícula es

${\displaystyle \frac{1}{2}m{\left(\frac{ds}{dt}+\frac{dx}{dt}\right)}^2=\frac{1}{2}m{\left(\frac{M}{m+M}\right)}^2{s}_0^2{\omega }^2{\sin }^2\left(\omega t\right)}$

Sumando los tres términos, obtenemos la energía total constante del sistema aislado e igual a la energía inicial del muelle deformado s₀

${\displaystyle \frac{1}{2}k{s}_0^2}$

Actividades

Se introduce

• La masa M del bloque, en el control titulado Masa bloque
• La masa de la partícula se ha fijado en m=1 kg
• La constante elástica k del muelle, en el control titulado Constante muelle
• La partícula se desplaza s₀=0.5 m y se suelta

Se pulsa el botón titulado Nuevo

Observamos los movimientos de la partícula unida al muelle elástico y de la plataforma. En la parte central, un gráfico en forma de tarta nos da idea de como se reparte la energía total del sistema aislado: en color gris, la energía potencial del muelle deformado, en color azul la energía cinética de la plataforma y en color rojo, la energía cinética de la partícula

Ecuaciones de Lagrange

La energía potencial de la partícula unida a un muelle elástico de constante k es

${\displaystyle V=\frac{1}{2}k{s}^2}$

La energía cinética de la partícula y de la plataforma es

${\displaystyle \begin{array}{l}T=\frac{1}{2}m{\left(\frac{ds}{dt}+\frac{dx}{dt}\right)}^2+\frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2=\\ \frac{1}{2}m{\left(\frac{M}{m+M}\right)}^2{\left(\frac{ds}{dt}\right)}^2+\frac{1}{2}M{\left(-\frac{m}{m+M}\right)}^2{\left(\frac{ds}{dt}\right)}^2=\frac{1}{2}\frac{mM}{m+M}{\left(\frac{ds}{dt}\right)}^2\end{array}}$

La lagrangiana L=T-V es

${\displaystyle L=\frac{1}{2}\frac{mM}{m+M}{\left(\frac{ds}{dt}\right)}^2-\frac{1}{2}k{s}^2}$

La ecuación del movimiento en términos de la coordenada s es

${\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\frac{\partial L}{\partial \dot{s}}\right)-\frac{\partial L}{\partial s}=0\\ \frac{mM}{m+M}\frac{d^{2}s}{d{t}^2}+ks=0\end{array}}$

que es la misma ecuación diferencial que hemos obtenido aplicando la segunda ley de Newton