Consideremos la colisión elástica entre una partícula de masa m incidente con velocidad v₀ contra otra partícula de masa M que está en reposo.

• Por la conservación del momento lineal

mv₀=mv+MV

• Por la conservación de la energía

${\displaystyle \frac{1}{2}m{v}^2+\frac{1}{2}M{V}^2=\frac{1}{2}m{v}_0^2}$

La solución de este sistema de dos ecuaciones con dos incógnitas es

${\displaystyle \{\begin{array}{l}v=\frac{m-M}{m+M}{v}_0\\ V=\frac{2m}{m+M}{v}_0\end{array}}$

Cuando las partículas son idénticas M=m, v=0, y V=v₀. La primera partícula permenece en reposo después del choque. Hay un intercambio de momento lineal, la primera se lo cede a la segunda, quedando aquella en reposo.

Modelo de choque elástico

Consideremos una partícula de masa m choca con otra de masa M inicialmente en reposo. Antes del choque, la velocidad de la primera es v₀ y la segunda está en reposo.

Cuando las partículas entran en contacto en el instante t=0, consideramos que las partículas son dos partículas unidas por un muelle elástico de constante k y longitud l sin deformar. l=r₁+r₂ podría ser la distancia inicial entre los centros de dos bolas que chocan. Este ejemplo es similar al tratado en la página titulada Sistema aislado de dos partículas interactuantes

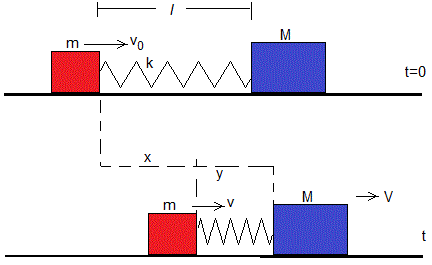
En el instante t, la posición de la partícula de masa m es x y su velocidad disminuye a v=dx/dt, y la posición de la partícula de masa M es y y su velocidad aumenta a V=dy/dt.

Movimiento del centro de masas

En un sistema aislado de dos partículas interactuantes, el centro de masas se mueve con velocidad constante

La posición inicial y la velocidad del centro de masas, t=0

${\displaystyle z_0=\frac{Ml}{M+m}{v}_{cm}=\frac{0+m{v}_0}{m+M}=\frac{m}{m+M}{v}_0}$

La posición del centro de masas en el instante t

${\displaystyle z=\frac{Ml}{M+m}+\left(\frac{m}{m+M}{v}_0\right)t}$

Movimiento relativo de las dos partículas

En el instante t, el muelle se ha deformado l-(y-x) y ejerce fuerzas iguales y de sentido contario sobre ambas partículas. Las ecuaciones del movimiento son.

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-k\left(l-(y-x)\right)\\ M\frac{d^{2}y}{d{t}^2}=k\left(l-(y-x)\right)\end{array}}$

Multiplicamos la primera por M, la segunda por m y restamos

${\displaystyle \begin{array}{l}mM\left(\frac{d^{2}y}{d{t}^2}-\frac{d^{2}x}{d{t}^2}\right)=k(m+M)\left(l-(y-x)\right)\\ \frac{mM}{m+M}\frac{d^2\xi }{d{t}^2}=k(l-\xi ),\xi =y-x\\ \frac{d^2\xi }{d{t}^2}+\frac{k}{\mu }\xi =\frac{k}{\mu }l\end{array}}$

donde ξ=y-x es la posición relativa de las dos partículas y μ=mM/(m+M) es la masa reducida del sistema formado por las dos partículas. El movimiento relativo de las dos partículas es equivalente al de una partícula de masa reducida μ que describe una oscilación libre

La solución de esta ecuación diferencial, es

${\displaystyle \begin{array}{l}\xi =l+A\sin (\omega t)+B\cos (\omega t)\omega =\sqrt{\frac{k}{\mu }}=\sqrt{\frac{k(m+M)}{mM}}\hfill \\ \frac{d\xi }{dt}=A\omega \cos (\omega t)-B\omega \sin (\omega t)\hfill \end{array}}$

Las constantes A y B se determinan a partir de las condiciones iniciales.

${\displaystyle t=0\{\begin{array}{l}\xi =l+B\\ \frac{d\xi }{dt}=A\omega \end{array}}$

• la posición inicial de las partículas es x=0, y=l, por lo que ξ=y-x=l. El coeficiente B=0

• la velocidad inicial de las partículas es dx/dt=v₀, dy/dt=0, por lo que dξ/dt=-v₀. El coeficiente A=-v₀/ω

El resultado es

${\displaystyle \begin{array}{l}\xi =l-\frac{v_0}{\omega }\sin (\omega t)\\ \frac{d\xi }{dt}=-v_0\cos (\omega t)\end{array}}$

Cuando ωt=π, ξ=l. El muelle recupera su longitud inicial sin deformar y-x=l, el choque ha terminado. La duración del choque es t=π/ω. La velocidad final de la partícula de masa reducida es v₀

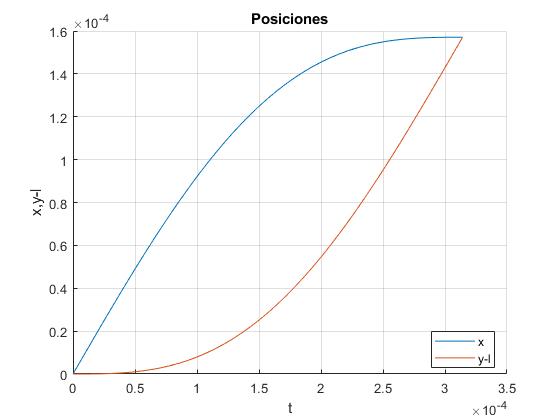
Posiciones

Conocida la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=y-x de las partículas, despejamos la posición x e y de cada una de las partículas en función del tiempo t.

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{mx+My}{m+M}=\frac{Ml}{M+m}+\frac{m}{m+M}{v}_{0}t\\ y-x=l-\frac{v_0}{\omega }\sin (\omega t)\end{array}\\ \{\begin{array}{l}x=\frac{v_0}{m+M}\left(mt+\frac{M}{\omega }\sin (\omega t)\right)\\ y=l+\frac{m}{m+M}{v}_0\left(t-\frac{1}{\omega }\sin (\omega t)\right)\end{array}\end{array}}$

Ejemplo

• Masa de la primera bola, m=0.1 kg
• Velocidad antes del choque, v₀=1 m/s
• Masa de la segunda bola, M=0.1 kg
• Velocidad antes del choque, en reposo
• Constante elástica del muelle, k=5·10⁶ N/m

La frecuencia angular ω=10 000 rad/s y la duración del choque, t=0.314 ms

Representamos las posición x del centro de la primera bola y la posición y-l de la segunda

m=0.1; %masa primera bola
M=0.1; %masa segunda bola
v0=1; %velocidad inicial de la primera bola
k=5e6; %constante elástica del muelle

w=sqrt(k*(m+M)/(m*M)); %frecuencia angular
x=@(t) v0*(m*t+M*sin(w*t)/w)/(m+M); %posción x
y=@(t) m*v0*(t-sin(w*t)/w)/(m+M); %posición y-l
hold on
fplot(x,[0,pi/w])
fplot(y,[0,pi/w])
hold off
xlabel('t')
ylabel('x,y-l')
legend('x','y-l','Location','best')
grid on
title('Posiciones')

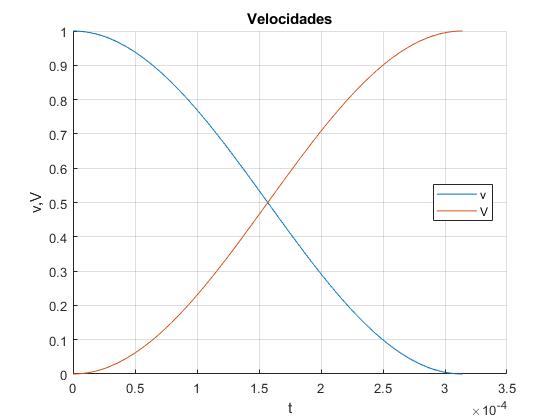
Velocidades

Derivando respecto del tiempo obtenemos las velocidades

${\displaystyle \{\begin{array}{l}v=\frac{dx}{dt}=\frac{v_0}{m+M}\left(m+M\cos (\omega t)\right)\\ V=\frac{dy}{dt}=\frac{m}{m+M}{v}_0\left(1-\cos (\omega t)\right)\end{array}}$

Cuando termina el choque, t=π/ω. Las velocidades son

${\displaystyle \{\begin{array}{l}v=\frac{m-M}{m+M}{v}_0\\ V=\frac{2m}{m+M}{v}_0\end{array}}$

Resultado que hemos obtenido al principio de la página

Representamos las velocidades v y V en función del tiempo t para el ejemplo anterior

m=0.1; %masa primera bola
M=0.1; %masa segunda bola
v0=1; %velocidad inicial de la primera bola
k=5e6; %constante elástica del muelle

w=sqrt(k*(m+M)/(m*M)); %frecuencia angular
v=@(t) v0*(m+M*cos(w*t))/(m+M);
V=@(t) m*v0*(1-cos(w*t))/(m+M);
hold on
fplot(v,[0,pi/w])
fplot(V,[0,pi/w])
hold off
xlabel('t')
ylabel('v,V')
grid on
legend('v','V','Location','best')
title('Velocidades')

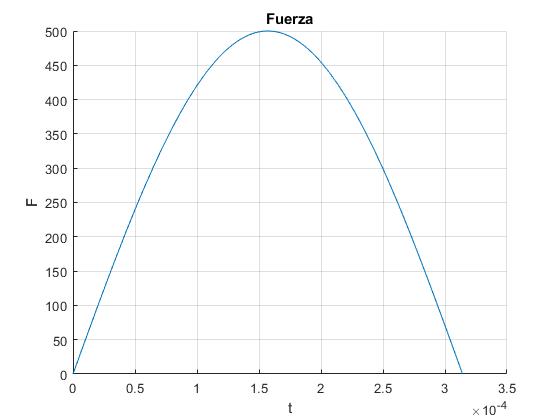
Fuerza

La fuerza que ejerce el muelle deformado sobre cada una de las partículas es k(l-(y-x))

${\displaystyle F=\frac{k{v}_0}{\omega }\sin (\omega t)}$

Representamos la fuerza F en función del tiempo t, con los datos del ejemplo

m=0.1; %masa primera bola
M=0.1; %masa segunda bola
v0=1; %velocidad inicial de la primera bola
k=5e6; %constante elástica del muelle

w=sqrt(k*(m+M)/(m*M)); %frecuencia angular
F=@(t) k*v0*sin(w*t)/w;
hold on
fplot(F,[0,pi/w])
hold off
xlabel('t')
ylabel('F')
grid on
title('Fuerza')

El impulso es el área bajo la curva

${\displaystyle I={\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}F·dt}=\frac{k{v}_0}{\omega }{\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}\sin (\omega t)·dt}=2\frac{k{v}_0}{{\omega }^2}=2\mu v_0}$

La velocidad inicial de la partícula de masa reducida μ es -v₀ y la velocidad final es v₀, el cambio de momento lineal es 2μv₀

Con los datos del ejemplo, el impulso es I=0.1 N·s

El trabajo W de la fuerza que ejece el muelle es nulo. La energía cinética de la partícula de masa reducida no cambia. En un muelle elástico la fuerza y el desplazamiento tiene signos contrarios

${\displaystyle W=-{\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}F·d\xi }=-{\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}F·\frac{d\xi }{dt}dt}=\frac{k{v}_0^2}{\omega }{\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}\sin (\omega t)·\cos (\omega t)dt}=-\frac{1}{4}\frac{k{v}_0^2}{{\omega }^2}{\cos (2\omega t)|}_0^{\pi /\omega }=0}$

Actividades

Se introduce

• la masa m de la primera bola de color azul en kg, en el control titulado Masa m
• la constante k del muelle elástico, en el control titulado Constante

Se ha fijado

• la masa de la segunda bola de color rojo, M=1 kg
• la velocidad de la primera bola, v₀=1 m/s
• la segunda bola está inicialmente en reposo
• las dos bolas tiene el mismo radio, 10 cm. La longitud del muelle sin deformar l=0.2 m

Se pulsa el botón titulado Nuevo

Se muestra de forma animada las tres etapas del movimiento de las dos bolas

1. La inicial, la primera bola se mueve con velocidad v₀ y la segunda está en reposo. Esta etapa termina cuando entran en contacto
2. La intermedia, el movimiento de las dos bolas durante el intervalo de tiempo que dura el choque
3. La final, las dos bolas se mueven con velocidad constante después del choque

Se observa la bola de color azul moviéndose hacia la derecha, hasta que entra en contacto con la bola de color rojo. Se observa que los centros de las dos bolas están unidos por un muelle de longitud l

Durante el tiempo que dura el choque los centros de las bolas se desplazan y el muelle se deforma. Observamos las fuerzas que ejerce el muelle, iguales y de sentido contrario, sobre el centro de las bolas

Cuando el muelle recupera su longitud inicial l en el instante t=π/ω, observamos las bolas desplazándose con velocidad constante v y V, que son las que se obtienen de las dos ecuaciones que describen el choque elástico

Para que se aprecie las tres etapas del movimiento de las bolas, la constante elástica k del muelle tiene que ser pequeña

En la parte superior, vemos como se distribuye la energía total constante en cada una de las tres etapas del movimiento

Choque completamente inelástico

Consideremos el choque completamente inelástico entre una partícula de masa m incidente con velocidad v₀ contra otra partícula de masa M que está en reposo.

• Por la conservación del momento lineal

${\displaystyle \begin{array}{l}m{v}_0=(m+M)v\\ v=\frac{m}{m+M}{v}_0\end{array}}$

• Balance energético

${\displaystyle \Delta E=\frac{1}{2}(m+M)v^2-\frac{1}{2}m{v}_0^2=-\frac{1}{2}\frac{mM}{m+M}{v}_0^2=-\frac{1}{2}\mu v_0^2}$

Es la energía que se pierde en la colisión

Movimiento del centro de masas

En un sistema aislado de dos partículas interactuantes, el centro de masas se mueve con velocidad constante

La posición inicial y la velocidad del centro de masas, t=0

${\displaystyle z_0=\frac{Ml}{M+m}{v}_{cm}=\frac{0+m{v}_0}{m+M}=\frac{m}{m+M}{v}_0}$

La posición del centro de masas en el instante t

${\displaystyle z=\frac{Ml}{M+m}+\left(\frac{m}{m+M}{v}_0\right)t}$

Movimiento relativo de las dos partículas

En el instante t, el muelle se ha deformado l-(y-x) y ejerce fuerzas iguales y de sentido contrario sobre ambas partículas. Además, supondremos una fuerza de rozamiento proporcional a la velocidad relativa (dy/dt-dx/dt), como en las oscilaciones amortiguadas

${\displaystyle F=-k\left(l-(y-x)\right)+\lambda \left(\frac{dy}{dt}-\frac{dx}{dt}\right)}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-k\left(l-(y-x)\right)+\lambda \left(\frac{dy}{dt}-\frac{dx}{dt}\right)\hfill \\ M\frac{d^{2}y}{d{t}^2}=k\left(l-(y-x)\right)-\lambda \left(\frac{dy}{dt}-\frac{dx}{dt}\right)\hfill \end{array}}$

Multiplicamos la primera por M, la segunda por m y restamos

${\displaystyle \begin{array}{l}mM\left(\frac{d^{2}y}{d{t}^2}-\frac{d^{2}x}{d{t}^2}\right)=k(m+M)\left(l-(y-x)\right)-\lambda (m+M)\left(\frac{dy}{dt}-\frac{dx}{dt}\right)\hfill \\ \frac{mM}{m+M}\frac{d^2\xi }{d{t}^2}=k(l-\xi )-\lambda \frac{d\xi }{dt},\xi =y-x\hfill \\ \frac{d^2\xi }{d{t}^2}+2\gamma \frac{d\xi }{dt}+\frac{k}{\mu }\xi =\frac{k}{\mu }l\hfill \end{array}}$

donde ξ=y-x es la posición relativa de las dos partículas y μ=mM/(m+M) es la masa reducida del sistema formado por las dos partículas. El movimiento relativo de las dos partículas es equivalente al de una partícula de masa reducida μ que describe una oscilación amortiguada

Para que las partículas vayan juntas después del choque se requiere que

${\displaystyle {\gamma }^2>{\omega }_0^2=\frac{k}{\mu }}$

es decir, que la oscilación sea sobreamortiguada.

La solución de esta ecuación diferencial es

${\displaystyle \begin{array}{l}\xi =l+\exp (-\gamma t)\left\{A\sinh (\omega t)+B\cosh (\omega t)\right\}\\ {\omega }^2={\gamma }^2-{\omega }_0^2\end{array}}$

Derivando con respecto del tiempo

${\displaystyle \frac{d\xi }{dt}=-\gamma \exp (-\gamma t)\left\{A\sinh (\omega t)+B\cosh (\omega t)\right\}+\omega \exp (-\gamma t)\left\{A\cosh (\omega t)+B\sinh (\omega t)\right\}}$

Las constantes A y B se determinan a partir de las condiciones iniciales.

${\displaystyle t=0\{\begin{array}{l}\xi =l+B\\ \frac{d\xi }{dt}=-\gamma B+A\omega \end{array}}$

• la posición inicial de las partículas es x=0, y=l, por lo que ξ=y-x=l. El coeficiente B=0.

• la velocidad inicial de las partículas es dx/dt=v₀, dy/dt=0, por lo que dξ/dt=-v₀. El coeficiente A=-v₀/ω

El movimiento relativo se describe mediante la ecuación

${\displaystyle \begin{array}{l}\xi =l-\frac{v_0}{\omega }\exp (-\gamma t)\sinh (\omega t)\\ \frac{d\xi }{dt}=-\frac{v_0}{\omega }\exp (-\gamma t)\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)\end{array}}$

Cuando t=0, ξ=l y dξ/dt=-v₀. Cuando t→∞, ξ=l y dξ/dt=0

Posiciones

Conocida la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=y-x de las partículas, despejamos la posición x e y de cada una de las partículas en función del tiempo t.

${\displaystyle \{\begin{array}{l}\frac{mx+My}{m+M}=\frac{Ml}{M+m}+\frac{m}{m+M}{v}_{0}t\\ y-x=l-\frac{v_0}{\omega }\exp (-\gamma t)\sinh (\omega t)\end{array}}$

Despejamos x e y

${\displaystyle \{\begin{array}{l}x=\frac{v_0}{m+M}\left(mt+\frac{M}{\omega }\exp (-\gamma t)\sinh (\omega t)\right)\\ y=l+\frac{m}{m+M}{v}_0\left(t-\frac{1}{\omega }\exp (-\gamma t)\sinh (\omega t)\right)\end{array}}$

Ejemplo

• Masa de la primera bola, m=0.1 kg
• Velocidad antes del choque, v₀=1 m/s
• Masa de la segunda bola, M=0.1 kg
• Velocidad antes del choque, en reposo
• Constante elástica del muelle, k=5·10⁶ N/m
• Coeficiente de amortiguamiento, γ=15 000 s^-1

La frecuencia angular ω₀=10 000 rad/s. El coeficiente de amortiguamiento γ>ω₀ para que la oscilación sea sobreamortiguada

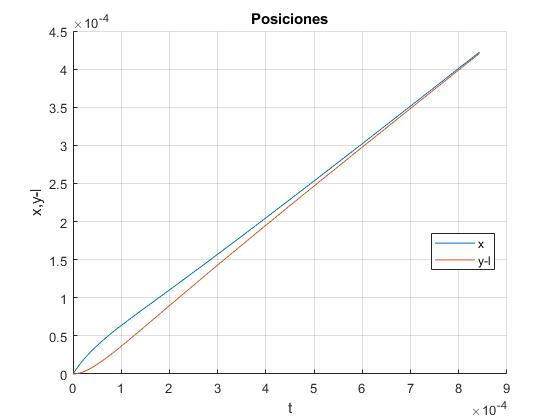
Representamos las posición x del centro de la primera bola y la posición y-l de la segunda

m=0.1; %masa primera bola
M=0.1; %masa segunda bola
v0=1; %velocidad inicial de la primera bola
k=5e6; %constante elástica del muelle
g=15000; %coeficiente de amortiguamiento
w0=sqrt(k*(m+M)/(m*M)); %frecuencia angular, w0 < g (sobreamortiguada)
w=sqrt(g^2-w0^2); %frecuencia angular
x=@(t) v0*(m*t+M*exp(-g*t).*sinh(w*t)/w)/(m+M); %posción x
y=@(t) m*v0*(t-exp(-g*t).*sinh(w*t)/w)/(m+M); %posición y-l
hold on
fplot(x,[0,3*pi/w])
fplot(y,[0,3*pi/w])
hold off
xlabel('t')
ylabel('x,y-l')
legend('x','y-l','Location','best')
grid on
title('Posiciones')

Velocidades

Derivando respecto del tiempo obtenemos las velocidades

${\displaystyle \{\begin{array}{l}v=\frac{dx}{dt}=\frac{v_0}{m+M}\left(m+\frac{M}{\omega }\exp (-\gamma t)\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)\right)\\ V=\frac{dy}{dt}=\frac{m}{m+M}{v}_0\left(1-\frac{1}{\omega }\exp (-\gamma t)\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)\right)\end{array}}$

Después de un tiempo t→∞, las velocidades después del choque son

${\displaystyle \{\begin{array}{l}{v}_{\infty }=\frac{m{v}_0}{m+M}\\ V_{\infty }=\frac{m{v}_0}{m+M}\end{array}}$

Resultado que hemos obtenido al principio de este sección

Representamos las velocidades v y V en función del tiempo t para el ejemplo anterior

m=0.1; %masa primera bola
M=0.1; %masa segunda bola
v0=1; %velocidad inicial de la primera bola
k=5e6; %constante elástica del muelle
g=15000; %coeficiente de amortiguamiento
w0=sqrt(k*(m+M)/(m*M)); %frecuencia angular, w0 < g (sobreamortiguada)
w=sqrt(g^2-w0^2); %frecuencia angular
v=@(t) v0*(m+M*exp(-g*t).*(-g*sinh(w*t)+w*cosh(w*t))/w)/(m+M);
V=@(t) m*v0*(1-exp(-g*t).*(-g*sinh(w*t)+w*cosh(w*t))/w)/(m+M);
hold on
fplot(v,[0,3*pi/w])
fplot(V,[0,3*pi/w])
hold off
xlabel('t')
ylabel('v,V')
grid on
legend('v','V','Location','best')
title('Velocidades')

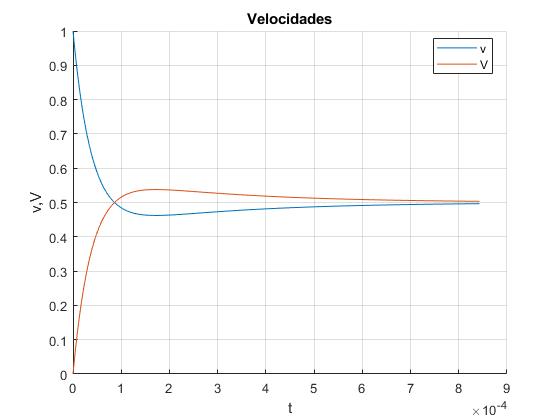
Como m=M, las velocidades finales tienden a, v_∞=V_∞=v₀/2

Fuerza

La fuerza que ejerce el muelle deformado sobre cada una de las partículas es

${\displaystyle \begin{array}{l}F=-k\left(l-(y-x)\right)+\lambda \left(\frac{dy}{dt}-\frac{dx}{dt}\right)=-k(l-\xi )+2\mu \gamma \frac{d\xi }{dt}=\\ -k\frac{v_0}{\omega }\exp (-\gamma t)\sinh (\omega t)-2\mu \gamma \frac{v_0}{\omega }\exp (-\gamma t)\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)\end{array}}$

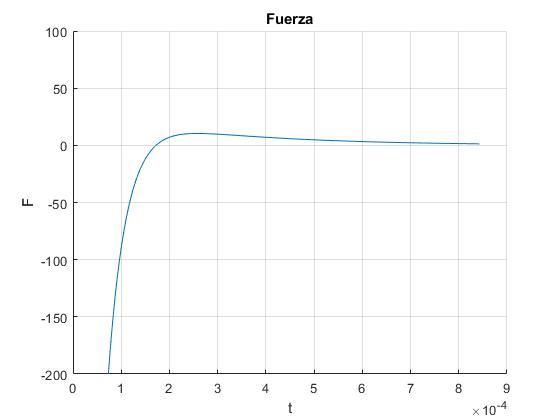
Representamos la fuerza F en función del tiempo t, con los datos del ejemplo

m=0.1; %masa primera bola
M=0.1; %masa segunda bola
mu=m*M/(m+M); %masa reducida
v0=1; %velocidad inicial de la primera bola
k=5e6; %constante elástica del muelle
g=15000; %coeficiente de amortiguamiento
w0=sqrt(k*(m+M)/(m*M)); %frecuencia angular, w0 < g (sobreamortiguada)
w=sqrt(g^2-w0^2); %frecuencia angular
F=@(t) -k*v0*exp(-g*t).*sinh(w*t)/w-2*mu*g*v0*exp(-g*t).*
(-g*sinh(w*t)+w*cosh(w*t))/w;
hold on
fplot(F,[0,3*pi/w])
hold off
xlabel('t')
ylabel('F')
grid on
title('Fuerza')

Impulso

${\displaystyle \begin{array}{l}I={\displaystyle \underset{0}{\overset{\infty }{\int }}F(t)dt}=\\ k\frac{v_0}{\omega }{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\gamma t)\sinh (\omega t)dt}-2\mu \gamma \frac{v_0}{\omega }\left\{-\gamma {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\gamma t)\sinh (\omega t)dt}+\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\gamma t)\cosh (\omega t)dt}\right\}\end{array}}$

Se integra por partes, el valor del integrando para el límite superior es cero, ya que γ>ω. Solamente tenemos que calcular el valor del integrando para el límite inferior, t=0. Calculamos el integrando con la ayuda de Math Symbolic de MATLAB

>> syms t g w;
>> assume(g,'positive')
>> assume(w,'positive')
>> assume(g>w)
>> int(exp(-g*t)*sinh(w*t),t)
ans =-(exp(- g*t - t*w)*(w - g + g*exp(2*t*w) + w*exp(2*t*w)))/(2*(g^2 - w^2))
>> simplify(ans)
ans =-(exp(-t*(g + w))*(w - g + g*exp(2*t*w) + w*exp(2*t*w)))/(2*(g^2 - w^2))
>> latex(ans)
ans =    '-\frac{{\mathrm{e}}^{-t\,\left(g+w\right)}\,\left(w-g+g\,
{\mathrm{e}}^{2\,t\,w}+w\,{\mathrm{e}}^{2\,t\,w}\right)}{2\,\left(g^2-w^2\right)}'

Copiamos el código y lo pegamos en MathType

${\displaystyle -\frac{{\text{e}}^{-t\left(g+w\right)}\left(w-g+g{\text{e}}^{2tw}+w{\text{e}}^{2tw}\right)}{2{\left(g^2-w^2\right)}^{\prime }}}$

Calculamos su valor cambiado de signo para t=0

El resultado final es

${\displaystyle I=k\frac{v_0}{\omega }\frac{\omega }{{\gamma }^2-{\omega }^2}-2\mu \gamma \frac{v_0}{\omega }\left\{-\gamma \frac{\omega }{{\gamma }^2-{\omega }^2}+\omega \frac{\gamma }{{\gamma }^2-{\omega }^2}\right\}=\frac{k{v}_0}{{\gamma }^2-{\omega }^2}=\frac{k{v}_0}{\frac{k}{\mu }}=\mu v_0}$

La velocidad inicial de la partícula de masa reducida μ es -v₀ y la velocidad final es 0, el cambio de momento lineal es μv₀

Trabajo

Calculamos el trabajo W de la fuerza F que ya no es nulo, ya que la energía cinética de la partícula de masa reducida cambia

${\displaystyle W=-{\displaystyle \underset{0}{\overset{\infty }{\int }}F(\xi )d\xi }=-{\displaystyle \underset{0}{\overset{\infty }{\int }}\left(-k(l-\xi )+2\mu \gamma \frac{d\xi }{dt}\right)\frac{d\xi }{dt}dt}=k{\displaystyle \underset{0}{\overset{\infty }{\int }}(l-\xi )\frac{d\xi }{dt}dt}-2\mu \gamma {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left(\frac{d\xi }{dt}\right)}^{2}dt}}$

El cálculo a mano es intenso por lo que procedemos del mismo modo que para el cálculo del impulso

${\displaystyle W=-2\mu \gamma {\left(\frac{v_0}{\omega }\right)}^2{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)}^{2}dt}-k\frac{v_0^2}{{\omega }^2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left(\exp (-\gamma t)\sinh (\omega t)\right)\exp (-\gamma t)\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)dt}}$

El primer término vale

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)}^{2}dt}=\\ {\gamma }^2{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\sinh }^2(\omega t)dt}+{\omega }^2{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\cosh }^2(\omega t)dt}-2\gamma \omega {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t)\cosh (\omega t)\sinh (\omega t)dt}=\\ {\gamma }^2\frac{{\omega }^2}{4\gamma \left({\gamma }^2-{\omega }^2\right)}+{\omega }^2\frac{2{\gamma }^2-{\omega }^2}{4\gamma \left({\gamma }^2-{\omega }^2\right)}-2\gamma \omega \frac{2\omega }{8\left({\gamma }^2-{\omega }^2\right)}=\frac{{\omega }^2}{4\gamma }\end{array}}$

El segundo término

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left(\exp (-\gamma t)\sinh (\omega t)\right)\exp (-\gamma t)\left(-\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right)dt}=\\ -\gamma {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\sinh }^2(\omega t)dt+\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t)\cosh (\omega t)\sinh (\omega t)dt}}=\\ -\gamma \frac{{\omega }^2}{4\gamma \left({\gamma }^2-{\omega }^2\right)}+\omega \frac{2\omega }{8\left({\gamma }^2-{\omega }^2\right)}=0\end{array}}$

El resultado es

${\displaystyle W=-2\mu \gamma {\left(\frac{v_0}{\omega }\right)}^2\frac{{\omega }^2}{4\gamma }=-\frac{1}{2}\mu v_0^2}$

La velocidad inicial de la partícula de masa reducida μ es -v₀ y la velocidad final es 0, su energía cinética disminuye

Actividades

Se introduce

• la masa m de la primera bola de color azul en kg, en el control titulado Masa m
• la constante γ de amortiguamiento, en el control titulado Constante. Para que la oscilación sea sobreamortiguada γ>ω₀. Se proporciona este dato en la parte superior derecha

Se ha fijado

• la masa de la segunda bola de color rojo, M=1 kg
• la velocidad de la primera bola, v₀=1 m/s
• la segunda bola está inicialmente en reposo
• las dos bolas tiene el mismo radio, 10 cm. La longitud del muelle sin deformar l=0.2 m
• la constante del muelle elástico, k=100 N/m

Se pulsa el botón titulado Nuevo

Se muestra de forma animada las tres etapas del movimiento de las dos bolas

1. La inicial, la primera bola se mueve con velocidad v₀ y la segunda está en reposo. Esta etapa termina cuando entran en contacto
2. La intermedia, el movimiento de las dos bolas durante el intervalo de tiempo que dura el choque
3. La final, las dos bolas se mueven con velocidad constante después del choque

Se observa la bola de color azul moviéndose hacia la derecha, hasta que entra en contacto con la bola de color rojo. Se observa que los centros de las dos bolas están unidos por un muelle de longitud l

Durante el tiempo que dura el choque los centros de las bolas se desplazan y el muelle se deforma. Observamos las fuerzas que ejerce el muelle, iguales y de sentido contrario, sobre el centro de las bolas

Cuando el muelle recupera su longitud inicial l en el instante t→∞, observamos las bolas desplazándose con velocidad constante v y V, que son las que se obtienen de las dos ecuaciones que describen el choque elástico

En la parte superior, vemos como se distribuye la energía total en cada una de las tres etapas del movimiento. En color negro, la energía disipada

Referencias

Rod Cross. Impact force between two colliding billiard balls. Phys. Educ. 55 (2020) 065002

Jonathan Bougie, Asim Gangopadhyaya. Conservation laws and energy transformations in a class of common physics problems. Am. J. Phys. 87 (11), November 2019, pp. 868-874. Sec. II, B1. KE dissipation in collision