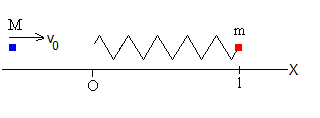
Consideremos una partícula de masa M, que lleva una velocidad v₀ y choca con un muelle de constante k unido a una partícula de masa m en reposo.

El choque se produce en el origen O, y la posición inicial de la partícula de masa m es l, la longitud del muelle sin deformar.

Después del choque las dos partículas se mueven unidas por el muelle elástico.

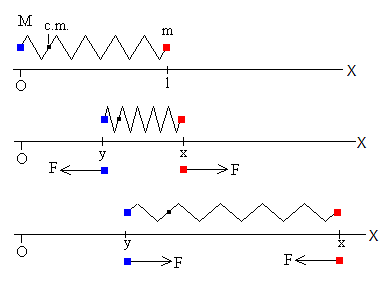
• en la parte superior, la situación inicial cuando el muelle está sin deformar.
• en la parte intermedia, cuando el muelle está comprimido. Como (x-y) es menor que l, la fuerza F es positiva para la partícula de la derecha (de masa m) y es negativa para la partícula de la izquierda (de masa M).
• en la parte inferior, cuando el muelle está estirado. Como (x-y) es mayor que l, la fuerza F es negativa para la partícula de la derecha (de masa m) y es positiva para la partícula de la izquierda (de masa M).

Ecuaciones del movimiento

Las ecuaciones del movimiento para cada una de las dos partículas son,

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=k\left(l-(x-y)\right)\\ M\frac{d^{2}y}{d{t}^2}=-k\left(l-(x-y)\right)\end{array}}$

• Movimiento del centro de masa

Si sumamos las dos ecuaciones tenemos

${\displaystyle m\frac{d^{2}x}{d{t}^2}+M\frac{d^{2}y}{d{t}^2}=0}$

La aceleración del c.m. es cero, el centro de masa se mueve con velocidad constante.

${\displaystyle \frac{dz}{dt}=\frac{M{v}_0}{m+M}}$

El movimiento del c.m. es uniforme, su posición es z=z₀+v_cm·t, donde z₀ es la posición inicial en el instante t=0.

${\displaystyle z=\frac{ml}{m+M}+\frac{M{v}_0}{m+M}t}$

• Movimiento relativo de las dos partículas

Multiplicando la primera ecuación diferencial por M y la segunda por m y restando ambas ecuaciones diferenciales obtenemos.

${\displaystyle \begin{array}{l}mM\left(\frac{d^{2}x}{d{t}^2}-\frac{d^{2}y}{d{t}^2}\right)=(m+M)k\left(l-(x-y)\right)\\ \frac{mM}{m+M}\left(\frac{d^2\xi }{d{t}^2}\right)=k\left(l-\xi \right)\end{array}}$

donde ξ=x-y es la posición relativa de las dos partículas. Esta ecuación nos dice que el movimiento relativo de las dos partículas es equivalente al movimiento de una partícula de masa reducida μ=mM/(m+M) bajo la acción de la fuerza que describe la interacción mutua F=k(l-ξ).

${\displaystyle \frac{d^2\xi }{d{t}^2}+\frac{k}{\mu }\xi =\frac{k}{\mu }l}$

La solución de esta ecuación diferencial, como puede comprobarse por simple sustitución es la suma de la solución particular l y de la solución de la ecuación diferencial homogénea, Asin(ωt)+Bcos(ωt)

${\displaystyle \begin{array}{l}\xi =l+A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\\ \omega =\sqrt{\frac{k}{\mu }}=\sqrt{\frac{k(m+M)}{mM}}\end{array}}$

Las constantes A y B se determinan a partir de las condiciones iniciales. En el instante t=0,

• la posición de las partículas es x=l, y=0, por lo que ξ=x-y=l.

• la velocidad inicial de las partículas es dy/dt=v₀, dx/dt=0, por lo que dξ/dt=-v₀

${\displaystyle \xi =l-\frac{v_0}{\omega }\sin \left(\omega t\right)}$

Movimiento de cada una de las dos partículas

Conocemos la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=x-y de las partículas en función del tiempo t.

${\displaystyle \begin{array}{l}z=\frac{mx+My}{m+M}=\frac{ml}{m+M}+\frac{M{v}_0}{m+M}t\\ \xi =x-y=l-\frac{v_0}{\omega }\sin \left(\omega t\right)\end{array}}$

Despejamos x e y de este sistema de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}x=l+\frac{M{v}_0}{m+M}\left(t-\frac{\sin \left(\omega t\right)}{\omega }\right)\\ y=\frac{v_0}{m+M}\left(Mt+m\frac{\sin \left(\omega t\right)}{\omega }\right)\end{array}}$

Comprobamos que en el instante t=0, las posiciones iniciales son x=l, y=0.

Creamos el siguiente script para representar las posiciones x e y de cada una de las dos partículas y del c.m. z en función del tiempo

k=5;    %constante elástica del muelle
M=2;  %masa izquierda
m=1; %masa derecha
lonMuelle=2; %longitud del muelle sin deformar
v0=2; %velocidad inicial
w=sqrt(k*(m+M)/(m*M));

x=@(t) lonMuelle+M*v0*(t-sin(w*t)/w)/(m+M);
y=@(t) v0*(M*t+m*sin(w*t)/w)/(m+M);
z=@(t) (m*x(t)+M*y(t))/(m+M);  %centro de masa
hold on
fplot(y,[0,6])
fplot(x,[0,6])
fplot(z,[0,6])
hold off
legend('izquierda','derecha','cm','Location','northwest')
xlabel('t(s)')
ylabel('y,x,z(m)')
title('Sistema aislado de dos partículas')
grid on

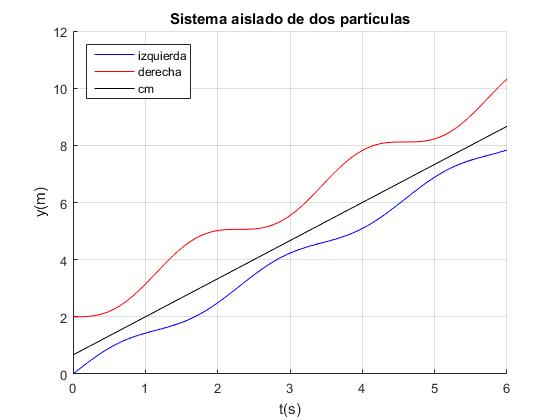
Calculamos el instante en el que la partícula de masa m llega a la posición x=10. Con los datos, k=5, M=2, m=1, l=2, resolvemos la ecuación transcendente empleando la función fzero

>> f=@(t) 6-t+sin(w*t)/w;
>> fzero(f,6)
ans =    5.8693

Las velocidades de las partículas en cualquier instante t son

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{M{v}_0}{m+M}\left(1-\cos \left(\omega t\right)\right)\\ \frac{dy}{dt}=\frac{v_0}{m+M}\left(M+m\cos \left(\omega t\right)\right)\end{array}}$

Comprobamos que en el instante t=0, las velocidades iniciales son dy/dt=v₀, dx/dt=0

Creamos el siguiente script para representar las velocidades dx/dt y dy/dt de cada una de las dos partículas en función del tiempo t

k=5;    %constante elástica del muelle
M=2;  %masa izquierda
m=1; %masa derecha
lonMuelle=2; %longitud del muelle sin deformar
v0=2; %velocidad inicial
w=sqrt(k*(m+M)/(m*M));

vx=@(t) M*v0*(1-cos(w*t))/(m+M);
vy=@(t) v0*(M+m*cos(w*t))/(m+M);

hold on
fplot(vy,[0,10])
fplot(vx,[0,10])
hold off
legend('izquierda','derecha','Location','northwest')
xlabel('t(s)')
ylabel('v_y, v_x')
title('Sistema aislado de dos partículas')
grid on

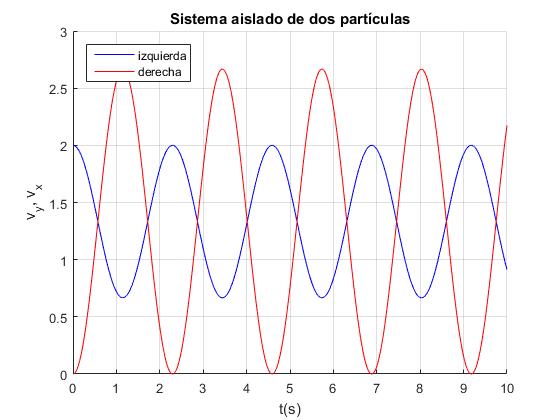
La partícula de masa m se detiene dx/dt=0, es decir, cuando cos(ωt)=1, ωt=0, 2π, 4π, etc.. Las posiciones de dicha partícula en estos instantes es

>> t=(0:2:6)*pi/w;
>> x=lonMuelle+M*v0*(t-sin(w*t)/w)/(m+M)
x =    2.0000    5.0591    8.1181   11.1772

Energías

La energía del sistema de partículas U es la suma de la energía cinética de la partícula de masa m, la energía cinética de la partícula de masa M, y la energía potencial del muelle deformado l-(x-y). Comprobamos después de hacer algunas operaciones que la suma es igual a la energía inicial de la partícula de masa M

${\displaystyle U=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}k{\left(l-(x-y)\right)}^2=\frac{1}{2}M{v}_0^2}$

Actividades

Se introduce

• La masa m de la partícula situada a la derecha (en color rojo) en el control titulado Masa derecha.
• La masa M de la partícula situada a la izquierda (en color azul), en el control titulado Masa izquierda.
• La velocidad inicial v₀ de la partícula de masa M (en color azul) en el control titulado Velocidad inicial
• La constante k del muelle elástico, en el control titulado Cte. muelle.
• La longitud l del muelle sin deformar está fijada por el programa interactivo en l=2 m

Se pulsa el botón titulado Nuevo.

Choque de un sistema de dos partículas con una pared rígida

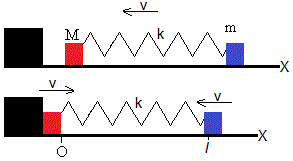
Dos partículas de masa M y m están unidas por un muelle elástico de longitud l y constante k. Se mueven sobre un plano horizontal sin rozamiento con la misma velocidad v.

La partícula de masa M choca elásticamente con una pared fija cambiando el sentido de su velocidad. Vamos a describir el movimiento de este sistema aislado de dos partículas

Se trata de una situación similar a la descrita, con condiciones iniciales diferentes

• Movimiento del centro de masas

La posición inicial del centro de masas

${\displaystyle \frac{ml}{m+M}}$

La velocidad constante del centro de masas es

${\displaystyle \frac{dz}{dt}=\frac{Mv+m(-v)}{m+M}=\frac{M-m}{m+M}v}$

La ecuación del movimiento del centro de masas es

${\displaystyle z=\frac{ml}{m+M}+\frac{M-m}{m+M}v·t}$

• Movimiento relativo de las dos partículas

${\displaystyle \begin{array}{l}\xi =l+A\sin (\omega t)+B\cos (\omega t)\hfill \\ \omega =\sqrt{\frac{k(m+M)}{mM}}\hfill \end{array}}$

Las constantes A y B se determinan a partir de las condiciones iniciales. En el instante t=0,

• la posición de las partículas es x=l, y=0, por lo que ξ=x-y=l.

• la velocidad inicial de las partículas es dy/dt=v, dx/dt=-v, por lo que dξ/dt=-2v

${\displaystyle \xi =l-\frac{2v}{\omega }\sin (\omega t)}$

Movimiento de cada una de las dos partículas

Conocemos la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=x-y de las partículas en función del tiempo t.

${\displaystyle \{\begin{array}{l}z=\frac{mx+My}{m+M}=\frac{ml}{m+M}+\frac{M-m}{m+M}v·t\\ \xi =x-y=l-\frac{2v}{\omega }\sin (\omega t)\end{array}}$

Despejamos x e y de este sistema de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}x=l+\frac{M-m}{m+M}v·t-\frac{M}{m+M}\frac{2v}{\omega }\sin (\omega t)\hfill \\ y=\frac{M-m}{m+M}v·t+\frac{m}{m+M}\frac{2v}{\omega }\sin (\omega t)\hfill \end{array}}$

Comprobamos que en el instante t=0, las posiciones iniciales son x=l, y=0.

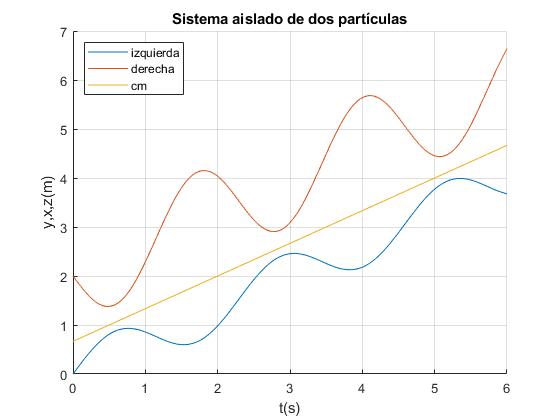
Creamos el siguiente script para representar las posiciones x e y de cada una de las dos partículas y del c.m. z en función del tiempo

k=5;    %constante elástica del muelle
M=2;  %masa izquierda
m=1; %masa derecha
lonMuelle=2; %longitud del muelle sin deformar
v=2; %velocidad inicial
w=sqrt(k*(m+M)/(m*M));

x=@(t) lonMuelle+(M-m)*v*t/(m+M)-M*2*v*sin(w*t)/((M+m)*w);
y=@(t) (M-m)*v*t/(m+M)+m*2*v*sin(w*t)/((M+m)*w);
z=@(t) (m*x(t)+M*y(t))/(m+M);  %centro de masa
hold on
fplot(y,[0,6])
fplot(x,[0,6])
fplot(z,[0,6])
hold off
legend('izquierda','derecha','cm','Location','northwest')
xlabel('t(s)')
ylabel('y,x,z(m)')
title('Sistema aislado de dos partículas')
grid on

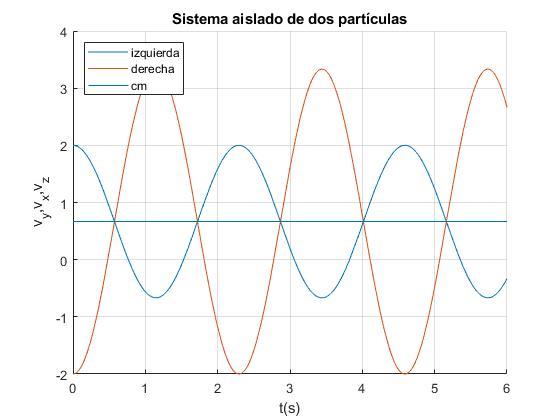
Las velocidades de las partículas en cualquier instante t son

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{M-m}{m+M}v-\frac{M}{m+M}2v\cos (\omega t)\\ \frac{dy}{dt}=\frac{M-m}{m+M}v+\frac{m}{m+M}2v\cos (\omega t)\end{array}}$

Creamos el siguiente script para representar las velocidades dx/dt y dy/dt de cada una de las dos partículas en función del tiempo t y la velocidad constante del centro de masas

k=5;    %constante elástica del muelle
M=2;  %masa izquierda
m=1; %masa derecha
lonMuelle=2; %longitud del muelle sin deformar
v=2; %velocidad inicial
w=sqrt(k*(m+M)/(m*M));

vx=@(t) (M-m)*v/(m+M)-M*2*v*cos(w*t)/(M+m);
vy=@(t) (M-m)*v/(m+M)+m*2*v*cos(w*t)/(M+m);
hold on
fplot(vy,[0,6])
fplot(vx,[0,6])
v_cm=(M-m)*v/(m+M);
line([0,6],[v_cm,v_cm])
hold off
legend('izquierda','derecha','cm','Location','northwest')
xlabel('t(s)')
ylabel('v_y,v_x,v_z')
title('Sistema aislado de dos partículas')
grid on

Energías

La energía del sistema de partículas U es la suma de la energía cinética de la partícula de masa m, la energía cinética de la partícula de masa M, y la energía potencial del muelle deformado l-(x-y). Comprobamos después de hacer algunas operaciones que la suma es igual a la energía inicial de la partículas de masa M y m que se mueven inicialmente con la misma velocidad v pero en sentidos contrarios

${\displaystyle U=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}k{\left(l-(x-y)\right)}^2=\frac{1}{2}M{v}^2+\frac{1}{2}m{v}^2}$

Choque de una partícula con un sistema de dos partículas

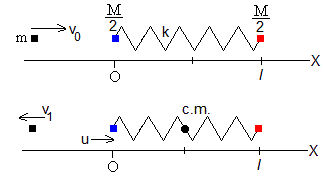
Una partícula de masa m que lleva una velocidad v₀ choca elásticamente contra un sistema formado por dos partículas de masa M/2 unidas por un muelle elástico de constante k, ambas partículas están inicialmente en reposo.

Inmediatamente después del choque, la partícula de masa M/2 adqiere una velocidad u y la partícula de masa m una velocidad v₁

Las ecuaciones del choque elástico son

${\displaystyle \begin{array}{l}\{\begin{array}{l}m{v}_0=m{v}_1+\frac{M}{2}u\\ \frac{1}{2}m{v}_0^2=\frac{1}{2}m{v}_1^2+\frac{1}{2}\frac{M}{2}{u}^2\end{array}\\ u=\frac{4m}{2m+M}{v}_0,v_1=\frac{2m-M}{2m+M}{v}_0\end{array}}$

Si m<M/2, la partícula de masa m retrocede v₁<0. En caso contrario, v₁>0, son posibles múltiples choques entre la partícula y el sistema de dos partículas iguales unidas por un muelle elástico

El centro de masas se mueve con velocidad constante u/2

${\displaystyle v_c=\frac{\frac{M}{2}u+\frac{M}{2}0}{\frac{M}{2}+\frac{M}{2}}=\frac{u}{2}=\frac{2m}{2m+M}{v}_0}$

La energía interna E_i del sistema de dos partículas es

${\displaystyle \begin{array}{l}{E}_i=\frac{1}{2}m{v}_0^2-\frac{1}{2}m{v}_1^2-\frac{1}{2}M{v}_c^2=\frac{2m^{2}M}{{\left(2m+M\right)}^2}{v}_0^2\\ \frac{E_i}{E_0}=\frac{4mM}{{\left(2m+M\right)}^2}=\frac{4r}{{\left(2r+1\right)}^2},r=\frac{m}{M}\end{array}}$

Representamos el cociente E_i/E₀ en función de r=m/M

f=@(x)  4*x./(2*x+1).^2;
fplot(f,[0,5])
line([0.5,0.5],[0,f(0.5)],'lineStyle','--')
grid on
xlabel('r=m/M')
ylabel('E_i/E_0')
title('Energía interna')

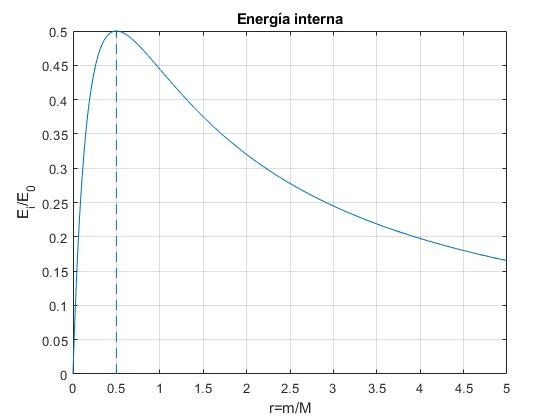
El cociente E_i/E₀ alcanza un máximo en r=0.5 como podemos ver en la figura. Derivando con respecto a r e igualando a cero.

${\displaystyle \begin{array}{l}\frac{4{\left(2r+1\right)}^2-2·2\left(2r+1\right)4r}{{\left(2r+1\right)}^4}=0\\ r^2=\frac{1}{4},r=\frac{1}{2}\end{array}}$

Movimiento de cada una de las dos partículas

Podemos describir el movimiento posterior del sistema de dos partículas, del mismo modo que hemos hecho en la sección anterior

• El centro de masas se mueve con velocidad constante u/2, desde la posición inicial l/2

${\displaystyle z=\frac{l}{2}+\frac{u}{2}t}$

• Movimiento relativo de las dos partículas

• la posición inicial de las partículas es x=l, y=0, por lo que ξ=x-y=l.

• la velocidad inicial de las partículas es dy/dt=u, dx/dt=0, por lo que dξ/dt=-u

${\displaystyle \begin{array}{l}\xi =x-y=l-\frac{u}{\omega }\sin (\omega t)\\ \omega =\sqrt{\frac{k}{\mu }}=\sqrt{\frac{k\left(\frac{M}{2}+\frac{M}{2}\right)}{\frac{M}{2}\frac{M}{2}}}=2\sqrt{\frac{k}{M}}\end{array}}$

Conocemos la posición z del c.m. y la posición relativa ξ=x-y de las partículas en función del tiempo t.

${\displaystyle \begin{array}{l}z=\frac{\frac{M}{2}x+\frac{M}{2}y}{\frac{M}{2}+\frac{M}{2}}=\frac{x+y}{2}\\ \{\begin{array}{l}x+y=l+u·t\\ x-y=l-\frac{u}{\omega }\sin (\omega t)\end{array}\end{array}}$

Despejamos x e y de este sistema de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}x=l+\frac{u}{2}t-\frac{u}{2\omega }\sin (\omega t)\\ y=\frac{u}{2}t+\frac{u}{2\omega }\sin (\omega t)\end{array}}$

Comprobamos que en el instante t=0, las posiciones iniciales son x=l, y=0.

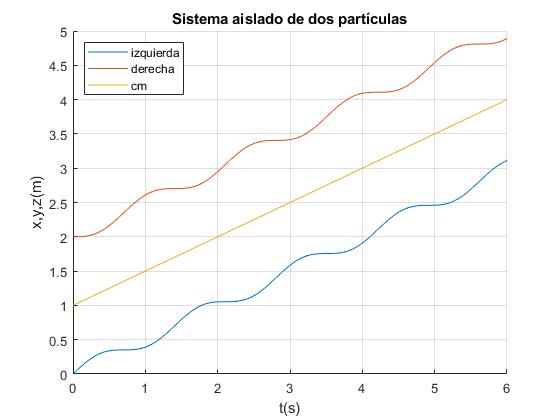
Creamos el siguiente script para representar las posiciones x e y de cada una de las dos partículas y del c.m. z en función del tiempo

k=5; %constante elástica del muelle
lonMuelle=2; %longitud del muelle sin deformar
u=1; %velocidad inicial
w=2*sqrt(k);

x=@(t) lonMuelle+u*t/2-u*sin(w*t)/(2*w);
y=@(t) u*t/2+u*sin(w*t)/(2*w);
z=@(t) lonMuelle/2+u*t/2;  %centro de masa
hold on
fplot(y,[0,6])
fplot(x,[0,6])
fplot(z,[0,6])
hold off
legend('izquierda','derecha','cm','Location','northwest')
xlabel('t(s)')
ylabel('x,y,z(m)')
title('Sistema aislado de dos partículas')
grid on

Energías

La energía del sistema de partículas U es la suma de la energía cinética de las dos partículas de masa M/2 y la energía potencial del muelle deformado l-(x-y). Comprobamos después de hacer algunas operaciones que la suma es igual a la energía inicial de la partícula de masa M/2 que se mueve con velocidad inicial u,

${\displaystyle \begin{array}{l}U=\frac{1}{2}\frac{M}{2}{u}^2=\frac{1}{4}M{u}^2\\ U=\frac{1}{2}\frac{M}{2}{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}\frac{M}{2}{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}k{\left(l-(x-y)\right)}^2=\\ \frac{1}{16}M{u}^2{\left(1-\cos \left(\omega t\right)\right)}^2+\frac{1}{16}M{u}^2{\left(1+\cos \left(\omega t\right)\right)}^2+\frac{1}{8}M{u}^2{\sin }^2\left(\omega t\right)=\frac{1}{4}M{u}^2\end{array}}$

Referencias

Physics Challenge for Teachers and Students Talking to the wall. The Physics Teacher. Vol. 48, December 2010, pp. 620

Vladimir Ivchenko. Collision of a Ball with a Stationary Oscillator. Phys. Teach. 58, 241 (2020), pp. 241