Un insecto camina sobre un anillo

Sea un anillo de radio r y masa m situado sobre un plano horizontal sobre el que puede deslizar sin rozamiento. Un insecto de masa M se mueve a lo largo del anillo

• Con velocidad angular cosntante ω
• Parte del origen en reposo y se mueve sobre el anillo con aceleración angular constante α

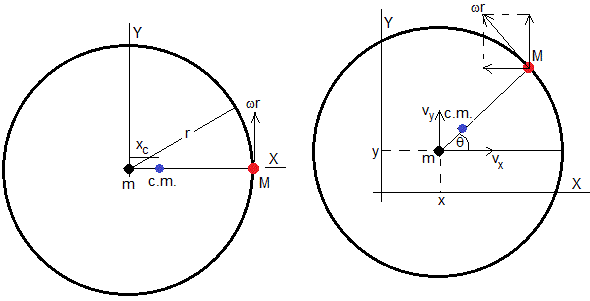
El centro de masa del anillo se encuentra en su centro, y el centro de masas del conjunto se encuentra

${\displaystyle x_{\mathrm{cm}}=\frac{M}{m+M}r}$

En la figura, a la izquierda, se encuentra la situación inicial. El centro del anillo parte del origen, y la velocidad inicial del insecto es ωr

En el instante t, el centro del anillo se encuentra en la posición (x,y), las componentes de su velocidad son v_x y v_y. El insecto se encuentra en la posición θ relativa al origen del anillo o bien, en la posición

${\displaystyle \{\begin{array}{l}x+r\cos \theta \\ y+r\sin \theta \end{array}}$

Las componentes de su velocidad son

${\displaystyle \{\begin{array}{l}{v}_x-\omega r\sin \theta \\ v_y+\omega r\cos \theta \end{array}}$

El insecto se mueve con velocidad angular constante

La posición del insecto en el anillo es θ=ωt

Dado que el sistema formado por el anillo y el insecto es aislado, se conserva el momento lineal

${\displaystyle \begin{array}{l}\{\begin{array}{l}m{v}_x+M\left(v_x-\omega r\sin \theta \right)=0\\ m{v}_y+M\left(v_y+\omega r\cos \theta \right)=M\omega r\end{array}\\ \frac{dx}{dt}=\frac{M}{M+m}\omega r\sin \left(\omega t\right),\frac{dy}{dt}=\frac{M}{M+m}\omega r\left(1-\cos \left(\omega t\right)\right)\end{array}}$

Integramos, sabiendo que en el instante t=0, x=0, y=0

${\displaystyle \begin{array}{l}x=\frac{M}{M+m}\omega r{\displaystyle \underset{0}{\overset{t}{\int }}\sin \left(\omega t\right)dt}=\frac{M}{M+m}r\left(1-\cos \theta \right)\\ y=\frac{M}{M+m}\omega r{\displaystyle \underset{0}{\overset{t}{\int }}\left(1-\cos \left(\omega t\right)\right)dt}=\frac{M}{M+m}\omega r\left(t-\frac{1}{\omega }\sin \left(\omega t\right)\right)=\frac{M}{M+m}r\left(\theta -\sin \theta \right)\end{array}}$

Posición del centro de masas

${\displaystyle \begin{array}{l}{x}_{cm}=\frac{mx+M\left(x+r\cos \theta \right)}{M+m}=x+\frac{M}{M+m}r\cos \theta =\frac{M}{M+m}r\\ y_{cm}=\frac{my+M\left(y+r\sin \theta \right)}{M+m}=y+\frac{M}{M+m}r\sin \theta =\frac{M}{M+m}r\omega t\end{array}}$

El centro de masas se mueve con velocidad constante a lo largo de la recta x=x_cm, paralela al eje Y

Actividades

Se introduce

• La masa m del anillo, en el control titulado Masa anillo
• La velocidad angular constante se ha fijado en ω=1 rad/s
• El radio del anillo se ha fijado en r=1 m
• La masa del insecto se ha fijado en M=1 kg

La circunferencia de color negro es el anillo, el punto de color rojo es el insecto, el punto de color negro es el centro del anillo y el punto de color azul es el centro de masas del sistema

En la parte superior izquierda, se proporcionan los datos del tiempo t en s y la posición angular θ en rad del insecto en el anillo

El insecto se mueve con aceleración angular constante

El insecto parte del origen en reposo, se mueve a lo largo del anillo con una velocidad se incrementa linealmente con el tiempo

${\displaystyle \omega =\alpha t,\theta =\frac{1}{2}\alpha t^2}$

Conservación del momento lineal

${\displaystyle \begin{array}{l}\{\begin{array}{l}m{v}_x+M\left(v_x-\omega r\sin \theta \right)=0\\ m{v}_y+M\left(v_y+\omega r\cos \theta \right)=0\end{array}\\ \frac{dx}{dt}=\frac{M}{M+m}r\alpha t\sin \left(\frac{1}{2}\alpha t^2\right),\frac{dy}{dt}=-\frac{M}{M+m}r\alpha t\cos \left(\frac{1}{2}\alpha t^2\right)\end{array}}$

Integramos, sabiendo que en el instante t=0, x=0, y=0

${\displaystyle \begin{array}{l}x=\frac{M}{M+m}r\alpha {\displaystyle \underset{0}{\overset{t}{\int }}t\sin \left(\frac{1}{2}\alpha t^2\right)dt}={\frac{M}{M+m}r\alpha \frac{1}{\alpha }\left(-\cos \left(\frac{1}{2}\alpha t^2\right)\right)|}_0^t=\frac{M}{M+m}r\left(1-\cos \theta \right)\\ y=-\frac{M}{M+m}r\alpha {\displaystyle \underset{0}{\overset{t}{\int }}t\cos \left(\frac{1}{2}\alpha t^2\right)dt}=-\frac{M}{M+m}r\sin \theta \end{array}}$

Posición del centro de masas

${\displaystyle \begin{array}{l}{x}_{cm}=\frac{mx+M\left(x+r\cos \theta \right)}{M+m}=x+\frac{M}{M+m}r\cos \theta =\frac{M}{M+m}r\\ y_{cm}=\frac{my+M\left(y+r\sin \theta \right)}{M+m}=y+\frac{M}{M+m}r\sin \theta =0\end{array}}$

Permanece fijo, en la posición (x_cm,0)

Actividades

Se introduce

• La masa m del anillo, en el control titulado Masa anillo
• La aceleración angular se ha fijado en α=0.05 rad/s²
• El radio del anillo se ha fijado en r=1 m
• La masa del insecto se ha fijado en M=1 kg

La circunferencia de color negro es el anillo, el punto de color rojo es el insecto, el punto de color negro es el centro del anillo y el punto de color azul es el centro de masas del sistema

En la parte superior izquierda, se proporcionan los datos del tiempo t en s y la posición angular θ en rad del insecto en el anillo

Sistema de tres partículas (I)

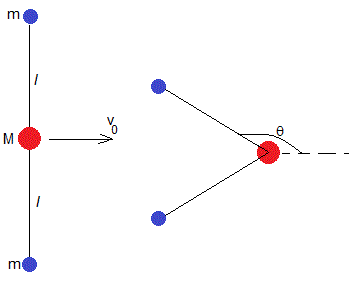
Sea un sistema aislado formado por una partícula de masa M y dos partículas iguales de masa m, unidas a la primera mediante una varilla rígida de longitud l y de masa despreciable.

A la izquierda de la figura, se muestra la situación inicial, a la partícula de masa M se le proporciona una velocidad inicial v₀. A la derecha de la figura, se muestra la situación en el instante t.

En un sistema aislado, la velocidad del centro de masas se mantiene contante

${\displaystyle V_c=\frac{M}{M+2m}{v}_0}$

La posición del centro de masas es el de una partícula en movimiento rectilíneo y uniforme

${\displaystyle X_c=V_{c}t=\frac{M}{M+2m}{v}_{0}t}$

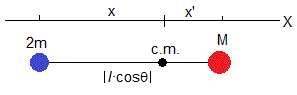
Establecemos el origen en el centro de masas. Se cumple que

• La posición de la partícula de masa m es (x, y=lsinθ)
• La posición de la partícula de masa M es (x', 0)

${\displaystyle \begin{array}{l}\{\begin{array}{l}2mx+Mx\text{'}=0\\ -x+x\text{'}=\left|l\cos \theta \right|\end{array}\\ x\text{'}=\frac{2m}{M+2m}\left|l\cos \theta \right|=-\frac{2m}{M+2m}l\cos \theta ,\frac{\pi }{2}\le \theta <\pi \\ x=-\frac{M}{M+2m}\left|l\cos \theta \right|=\frac{M}{M+2m}l\cos \theta \end{array}}$

La partícula de masa m describe una trayectoria elíptica en el Sistema de Referencia del centro de masas

${\displaystyle \begin{array}{l}\{\begin{array}{l}l\cos \theta =\frac{M+2m}{M}x\\ l\sin \theta =y\end{array}\\ \frac{x^2}{{\left(\frac{M}{M+2m}l\right)}^2}+\frac{y^2}{l^2}=1\end{array}}$

La energía cinética inicial del sistema de tres partículas respecto del c.m. es

${\displaystyle E_k=\frac{1}{2}2m{\left(-V_c\right)}^2+\frac{1}{2}M{\left(v_0-V_c\right)}^2=\frac{Mm}{M+2m}{v}_0^2}$

La energía cinética del sistema de tres partículas respecto del c.m. en el instante t es

${\displaystyle E_k=\frac{1}{2}2m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)+\frac{1}{2}M{\left(\frac{dx\text{'}}{dt}\right)}^2=\frac{Mm}{M+2m}{v}_0^2}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}2m\frac{dx}{dt}+M\frac{dx\text{'}}{dt}=0\\ \frac{1}{2}2m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)+\frac{1}{2}M{\left(-\frac{2m}{M}\frac{dx}{dt}\right)}^2=\frac{Mm}{M+2m}{v}_0^2\\ \left(1+\frac{2m}{M}\right){\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2=\frac{M}{M+2m}{v}_0^2\end{array}}$

Teniendo en cuenta que la partícula de masa m describe una trayectoria elíptica

${\displaystyle {\left(\frac{M+2m}{M}\right)}^{2}x\frac{dx}{dt}+y\frac{dy}{dt}=0}$

La conservación de la energía se expresa

${\displaystyle \begin{array}{l}\left(\frac{M+2m}{M}\right){\left(-{\left(\frac{M}{M+2m}\right)}^2\frac{y}{x}\frac{dy}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2=\frac{M}{M+2m}{v}_0^2\\ {\left(\frac{dy}{dt}\right)}^2=\frac{\frac{M}{M+2m}{v}_0^2}{1+{\left(\frac{M}{M+2m}\right)}^3\frac{y^2}{x^2}}=\frac{\frac{M}{M+2m}{v}_0^2}{1+{\left(\frac{M}{M+2m}\right)}^3\frac{y^2}{\left(l^2-y^2\right){\left(\frac{M}{M+2m}\right)}^2}}=\frac{M}{M+2m}{v}_0^2\frac{l^2-y^2}{l^2-y^2+\frac{M}{M+2m}{y}^2}\\ {\left(\frac{dy}{dt}\right)}^2=\frac{M}{M+2m}{v}_0^2\frac{l^2-y^2}{l^2-\frac{2m}{M+2m}{y}^2}\end{array}}$

Despejamos dy/dt

${\displaystyle \begin{array}{l}\frac{dy}{dt}=\sqrt{\frac{M}{M+2m}}{v}_0\sqrt{\frac{l^2-y^2}{l^2-\frac{2m}{M+2m}{y}^2}}\\ \frac{dy}{dt}=\sqrt{1-k^2}{v}_0\sqrt{\frac{1-{\left(\frac{y}{l}\right)}^2}{1-k^2{\left(\frac{y}{l}\right)}^2}},k^2=\frac{2m}{M+2m}\end{array}}$

Como y=lsinθ, integramos θ entre π/2 y π. Véase la página titulada Integrales elípticas

${\displaystyle \begin{array}{l}l\cos \theta ·\frac{d\theta }{dt}=\sqrt{1-k^2}{v}_0\frac{\cos \theta }{\sqrt{1-k^2{\sin }^2\theta }}\\ {\displaystyle \underset{\pi /2}{\overset{\theta }{\int }}\sqrt{1-k^2{\sin }^2\theta }·d\theta }=\sqrt{1-k^2}\frac{v_0}{l}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ {\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{1-k^2{\sin }^2\theta }·d\theta }-{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-k^2{\sin }^2\theta }·d\theta }=\sqrt{1-k^2}\frac{v_0}{l}t\\ E\left(\theta ,k\right)-E(k)=\sqrt{1-k^2}\frac{v_0}{l}t\end{array}}$

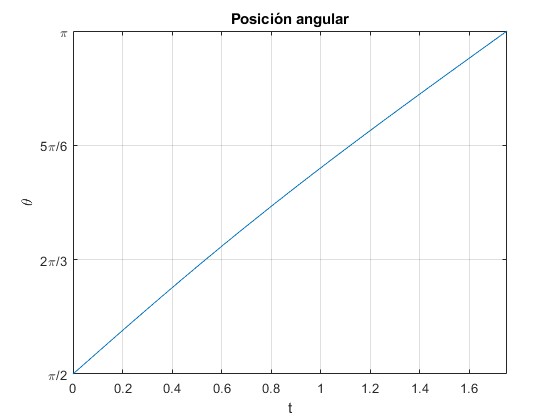
Representamos la función implícita del ángulo θ en función del tiempo t

M=4;
m=1;
k2=2*m/(M+2*m);
[K,E]=ellipke(k2);
f=@(x) (ellipticE(x,k2)-E)/sqrt(1-k2);
fplot(f, [pi/2,pi])
grid on
set(gca,'XTick',pi/2:pi/6:pi)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi'})
xlabel('\theta')
ylabel('t')
title('Posición angular')
view(90,-90)

Respecto del Sistema de Referencia de laboratorio los resultados son

• Posición de la partícula de masa m

${\displaystyle \begin{array}{l}Y=y=l·\sin \theta \\ X=V_{c}t+x=\frac{M}{M+2m}{v}_0\frac{E\left(\theta ,k\right)-E(k)}{\sqrt{1-k^2}\frac{v_0}{l}}+\frac{M}{M+2m}l\cos \theta \\ X=\frac{M}{M+2m}l\left(\frac{E\left(\theta ,k\right)-E(k)}{\sqrt{1-k^2}}+\cos \theta \right)\end{array}}$

• Posición de la partícula de masa M

${\displaystyle \begin{array}{l}X\text{'}=V_{c}t+x\text{'}=\frac{M}{M+2m}{v}_0\frac{E\left(\theta ,k\right)-E(k)}{\sqrt{1-k^2}\frac{v_0}{l}}t-\frac{2m}{M+2m}l\cos \theta =\\ \frac{1}{M+2m}\left(M\frac{E\left(\theta ,k\right)-E(k)}{\sqrt{1-k^2}}-2m\cos \theta \right)l\end{array}}$

Comprobamos que (2mX+MX')/(M+2m)=V_ct

• Velocidad de la partícula de masa m

${\displaystyle \begin{array}{l}{V}_y=\frac{dy}{dt}=\sqrt{1-k^2}{v}_0\frac{\cos \theta }{\sqrt{1-k^2{\sin }^2\theta }}\\ V_x=v_x+V_c=\frac{dx}{dt}+\frac{M}{M+2m}{v}_0=-\frac{y}{x}\frac{dy}{dt}{\left(\frac{M}{M+2m}\right)}^2+\frac{M}{M+2m}{v}_0\\ -\frac{l\sin \theta }{\frac{M}{M+2m}l\cos \theta }\sqrt{1-k^2}{v}_0\frac{\cos \theta }{\sqrt{1-k^2{\sin }^2\theta }}{\left(\frac{M}{M+2m}\right)}^2+\frac{M}{M+2m}{v}_0\\ V_x=\frac{M}{M+2m}{v}_0\left(1-\sqrt{1-k^2}\frac{\sin \theta }{\sqrt{1-k^2{\sin }^2\theta }}\right)\end{array}}$

V_x=0, V_y=0 en el instante t=0, θ=π/2

• Velocidad de la partícula de masa M

${\displaystyle \begin{array}{l}{V}_x^{\text{'}}=V_c+\frac{dx\text{'}}{dt}=\frac{M}{M+2m}{v}_0-\frac{2m}{M}\frac{dx}{dt}=\frac{M}{M+2m}{v}_0-\frac{2m}{M}\frac{dx}{dt}=\\ V_x^{\text{'}}=\frac{M}{M+2m}{v}_0\left(1+\frac{2m}{M}\sqrt{1-k^2}\frac{\sin \theta }{\sqrt{1-k^2{\sin }^2\theta }}\right)\end{array}}$

V'_x=v₀ en el instante t=0, θ=π/2

Comprobamos que el momento lineal es constante, 2mV_x+MV'_x=Mv₀

Comprobamos que la energía es constante e igual a la energía cinética inicial de la partícula de masa M

${\displaystyle \frac{1}{2}2m\left(V_x^2+V_y^2\right)+\frac{1}{2}MV{\text{'}}_x^2=\frac{1}{2}M{v}_0^2}$

M=4;
m=1;
v0=1;
k2=2*m/(M+2*m);
thh=linspace(pi/2,pi,10);
Vx=@(th) M*v0*(1-sqrt(1-k2)*sin(th)./sqrt(1-k2*sin(th).^2))/(M+2*m);
Vy=@(th) sqrt(1-k2)*v0*cos(th)./sqrt(1-k2*sin(th).^2);
Vp=@(th)  M*v0*(1+2*m*sqrt(1-k2)*sin(th)./(M*sqrt(1-k2*sin(th).^2)))/(M+2*m);
Ek=m*(Vx(thh).^2+Vy(thh).^2)+M*Vp(thh).^2/2;
disp(Ek) %energía
disp(M*v0^2/2)
p=2*m*Vx(thh)+M*Vp(thh);
disp(p) %momento lineal
disp(M*v0)

2.0000  2.0000  2.0000  2.0000  2.0000  2.0000  2.0000  2.0000  2.0000  2.0000
2
4.0000  4.0000  4.0000  4.0000  4.0000  4.0000  4.0000  4.0000  4.0000  4.0000
4

Sistema de tres partículas (II)

Dos bloques de masas 2m y 3m están conectados por una cuerda de longitud 2l. Ambos bloques deslizan sin rozamiento a la largo de una varilla horizontal. Un bloque de masa m está unido a la cuerda dividiéndola por la mitad, tal como se muestra en la figura.

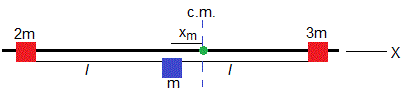
Situación inicial

En la situación inicial, la cuerda está horizontal y los bloques en reposo. Se libera el bloque de masa m situado en medio. Se pide calcular la velocidad de los bloques de masas 2m y 3m justo antes de chocar

En este sistema no hay fuerzas externas en la dirección horizontal. La posición x_cm del centro de masas no cambia. Situamos el origen en el centro de masas (punto de color verde).

${\displaystyle \begin{array}{l}2m(-l-x_m)+m(-x_m)+3m(l-x_m)=0\\ x_m=\frac{l}{6}\end{array}}$

• la distancia del centro de masas al bloque de masa m, es l/6
• la distancia del centro de masas al bloque de masa 2m, es 7l/6
• la distancia del centro de masas al bloque de masa 3m, es 5l/6

Situación en el instante t

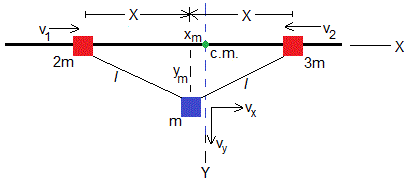
En el instante t, la posición del bloque intermedio de masa m es (-x_m,y_m)

Los bloques se han movido, pero la posición del centro de masas (punto de color verde) a lo largo del eje X no ha cambiado

${\displaystyle \begin{array}{l}2m(-X-x_m)+m(-x_m)+3m(X-x_m)=0\\ x_m=\frac{X}{6}\end{array}}$

Posiciones y velocidades

• bloque de masa (m): la posición horizontal es -x_m, la componente X de la velocidad, v_x=-dx_m/dt
• bloque de masa (m): la posición vertical y_m, la componente Y de la velocidad, v_y=dy_m/dt
• bloque de masa (2m): la posición es x₁=-X-x_m=-7x_m, la velocidad, v₁=dx₁/dt=-7dx_m/dt=7v_x
• bloque de masa (3m): la posición es x₂=X-x_m=5x_m, la velocidad, v₂=dx₂/dt=5dx_m/dt=-5v_x

Comprobamos la conservación del momento lineal a lo largo de la varilla (eje X)

${\displaystyle \begin{array}{l}2m{v}_1+3m(-v_2)+m{v}_x=0\\ 2m\left(7v_x\right)v_1+3m(-5v_x)+m{v}_x=0\end{array}}$

El sistema es conservativo, la energía total permanece constante

${\displaystyle mg(-y)+\frac{1}{2}(2m)v_1^2+\frac{1}{2}(3m)v_2^2+\frac{1}{2}m\left(v_x^2+v_y^2\right)=0}$

Las componentes v_x y v_y están relacionadas

${\displaystyle \begin{array}{l}{X}^2+y_m^2=l^2\\ X\frac{dX}{dt}+y_m\frac{d{y}_m}{dt}=\mathrm{0,}36x_m\frac{d{x}_m}{dt}+y_m\frac{d{y}_m}{dt}=0\\ -36x_m{v}_x+y_m{v}_y=0\end{array}}$

Situación final

Cuando x_m→0, y_m→l, v_y→0

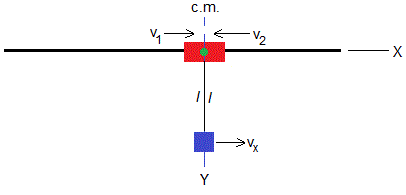
La conservación de la energía se escribe

${\displaystyle \begin{array}{l}mg(-l)+\frac{1}{2}(2m){\left(7v_x\right)}^2+\frac{1}{2}(3m){\left(-5v_x\right)}^2+\frac{1}{2}m{v}_x^2=0\\ v_x=\sqrt{\frac{gl}{87}},v_1=7\sqrt{\frac{gl}{87}},v_2=-5\sqrt{\frac{gl}{87}}\end{array}}$

Referencias

Physics Challenge for Teachers and Students. Squaring the circle: Now in 3D!. The Physics Teacher. Vol. 51, December 2013. pp. 567

David Morin. Introduction to Classical Mechanics With Problems and Solutions. Cambridge University Press (2007). Problema 5.53, pág. 184

LANG Jun，JIANG Fu-jin. Research on the trajectory equation and the cycle of the system of one rope with three balls. College Physics. 2017, 36(10): 24-28

Physics Challenge for Teachers and Students. No pun invented. The Physics Teacher Vol. 58, November 2020 pp. 599