Supongamos que utilizamos una cuerda elástica para tirar de una caja. Al principio, la cuerda no ejerce fuerza sobre la caja. A media que la goma se alarga, aumenta la fuerza sobre la caja inmóvil hasta que esta fuerza alcanza un valor límite determinado por el coeficiente de rozamiento estático. La caja se pone en movimiento, se acelera primero, hasta que la fuerza que ejerce la cuerda sea igual a la fuerza de rozamiento, luego, la caja decelera, disminuye su velocidad hasta que se para y comienza un nuevo ciclo.

El movimiento de la caja consta de dos fases:

• En la primera, la caja está en reposo y la energía suministrada por el operario se almacena en la cuerda en forma de energía elástica.

• En la segunda, la caja desliza, una parte de la energía almacenada se transforma en energía cinética y otra parte, se convierte en calor debido al trabajo de la fuerza de rozamiento.

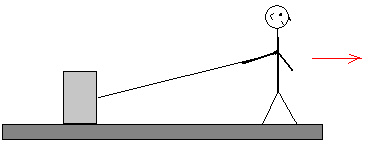
Se estudia el movimiento de una caja unida por una cuerda de cuyo extremo tira un operario:

• Que se mueve con velocidad constante, en esta página

• Con una fuerza constante, en la siguiente

En ambos casos, supondremos que la cuerda se comporta como un muelle elástico

El operario se mueve con velocidad constante.

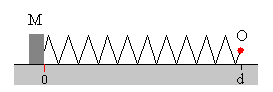
La masa de la caja es M, el muelle elástico de constante k tiene una longitud natural d. El coeficiente estático es μ_s y el coeficiente cinético μ_k≤ μ_s.

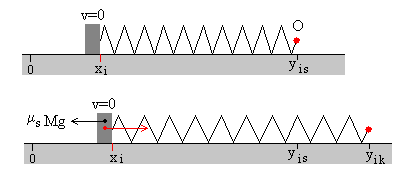
En la figura, se muestra la caja, el muelle elástico y el operario O en la situación inicial. La caja en el origen x=0, y el operario en la posición y=d.

La caja en reposo

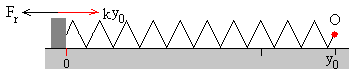
Cuando el operario se mueve hacia la derecha una distancia y del origen, el muelle se estira y la caja permanece en reposo en x=0. La fuerza de rozamiento F_r es igual a la fuerza que ejerce el muelle deformado k(y-d). En el momento en el que la fuerza de rozamiento alcanza su valor máximo μ_sMg, la caja empieza a deslizar.

La posición del operario es y₀ tal que k(y₀-d)= μ_sMg

En este instante ponemos en marcha el reloj, t=0

La caja desliza

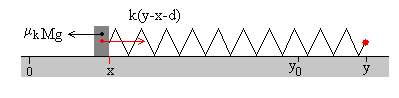
En un instante dado t, la caja se encuentra en la posición x y el operario se encuentra en la posición y

Las fuerzas sobre la caja en movimiento son:

• La fuerza que ejerce el muelle k(y-x-d)
• La fuerza de rozamiento F_r= μ_kMg

Las ecuaciones del movimiento de la caja y del operario son, respectivamente

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=k(y-x-d)-{\mu }_{k}Mg\\ y=y_0+vt\end{array}}$

La solución de la ecuación diferencial es

${\displaystyle x=A\sin (\omega t+\phi )+vt+y_0-d-\frac{{\mu }_{k}g}{{\omega }^2}{\omega }^2=\frac{k}{M}}$

La amplitud A y la fase φ se determina a partir de las condiciones iniciales

En el instante t=0, la caja parte de la posición x₀ con velocidad nula dx/dt=0

${\displaystyle A\cos \phi =-\frac{v}{\omega }A\sin \phi =-\left(y_0-x_0-d-\frac{{\mu }_{k}g}{{\omega }^2}\right)}$

La caja acelera primero y luego, decelera hasta que se detiene en el instante t,

${\displaystyle \frac{dx}{dt}=\omega A\cos (\omega t+\phi )+v=0t=\frac{4\pi -2\phi }{\omega }}$

La posición de la caja y la del operario en este instante es

${\displaystyle \begin{array}{l}x=2\left(y_0-d-\frac{{\mu }_{k}g}{{\omega }^2}\right)+v\left(\frac{4\pi -2\phi }{\omega }\right)-x_0\\ y=y_0+v\left(\frac{4\pi -2\phi }{\omega }\right)\end{array}}$

A partir de este momento, la caja permanece en reposo y volverá de deslizar cuando la fuerza de rozamiento alcance su valor máximo μ_sMg.

Etapas

La caja se mueve a tirones describiendo los ciclos. Las sucesivas posiciones de la caja en reposo x_i y del operario y_is (cuando la caja se para) e y_ik (cuando la caja empieza a deslizar) son:

• Primer ciclo

x₀=0, y_0s=d, la caja está en reposo en el origen, el operario a una distancia d del origen

La caja empieza a deslizar cuando el operario se encuentra en la posición y_0k tal que  k(y_0k-d)=µ_smg,

${\displaystyle y_{0k}=d+\frac{{\mu }_{s}g}{{\omega }^2}}$

Mientras la caja está en reposo, el operario se ha desplazado $y_{0k}-y_{0s}=\frac{{\mu }_{s}g}{{\omega }^2}$

La caja incrementa su velocidad, luego, disminuye hasta que se para, empleando un tiempo t=(4π-2φ)/ω desde que parte hasta que se detiene. Las posiciones de la caja y del operario son, respectivamente.

${\displaystyle \begin{array}{l}{x}_1=2\left(y_{0k}-d-\frac{{\mu }_{k}g}{{\omega }^2}\right)+vt-x_0=\frac{2{\mu }_{s}g}{{\omega }^2}-\frac{2{\mu }_{k}g}{{\omega }^2}+vt\\ y_{1s}=y_{0k}+vt=d+\frac{{\mu }_{s}g}{{\omega }^2}+vt\end{array}}$

• Segundo ciclo

La caja empieza a deslizar cuando el operario se encuentra en la posición y_1k tal que k(y_1k-x₁-d)=µ_smg

${\displaystyle y_{1k}=x_1+d+\frac{{\mu }_{s}g}{{\omega }^2}=\frac{3{\mu }_{s}g}{{\omega }^2}-\frac{2{\mu }_{k}g}{{\omega }^2}+vt+d}$

Mientras la caja está en reposo, el operario se desplazado $y_{1k}-y_{1s}=\frac{2{\mu }_{s}g}{{\omega }^2}-\frac{2{\mu }_{k}g}{{\omega }^2}$

La caja incrementa su velocidad, luego, disminuye hasta que se para, empleando un tiempo t=(4π-2φ)/ω desde que parte hasta que se detiene. Las posiciones de la caja y del operario son, respectivamente.

${\displaystyle \begin{array}{l}{x}_2=2\left(y_{1k}-d-\frac{{\mu }_{k}g}{{\omega }^2}\right)+vt-x_1=\frac{4{\mu }_{s}g}{{\omega }^2}-\frac{4{\mu }_{k}g}{{\omega }^2}+2vt\\ y_{2s}=y_{1k}+vt=\frac{3{\mu }_{s}g}{{\omega }^2}-\frac{2{\mu }_{k}g}{{\omega }^2}+2vt+d\end{array}}$

• Tercer ciclo

La caja empieza a deslizar cuando el operario se encuentra en la posición y_2k tal que k(y_2k-x₂-d)=µ_smg

${\displaystyle y_{2k}=x_2+d+\frac{{\mu }_{s}g}{{\omega }^2}=\frac{5{\mu }_{s}g}{{\omega }^2}-\frac{4{\mu }_{k}g}{{\omega }^2}+2vt+d}$

Mientras la caja está en reposo, el operario se desplazado $y_{2k}-y_{2s}=\frac{2{\mu }_{s}g}{{\omega }^2}-\frac{2{\mu }_{k}g}{{\omega }^2}$

La caja incrementa su velocidad, luego, disminuye hasta que se para, empleando un tiempo t=(4π-2φ)/ω desde que parte hasta que se detiene. Las posiciones de la caja y del operario son, respectivamente.

${\displaystyle \begin{array}{l}{x}_3=2\left(y_{2k}-d-\frac{{\mu }_{k}g}{{\omega }^2}\right)+vt-x_2=\frac{6{\mu }_{s}g}{{\omega }^2}-\frac{6{\mu }_{k}g}{{\omega }^2}+3vt\\ y_{3s}=y_{2k}+vt=\frac{5{\mu }_{s}g}{{\omega }^2}-\frac{4{\mu }_{k}g}{{\omega }^2}+3vt+d\end{array}}$

y así, sucesivamente

muEst=0.75; %coeficiente estático
muDin=0.5; %coeficiente cinético
k=20; %constante del muelle
vY=1; %velocidad constante del operario
    
w=sqrt(k);  %frecuencia angular
x0=0.0; %posición inicial de la caja
d=2; %posición inicial del operario
y0=d; %posición inicial del operario
y=y0; %posición  del operario

t=0;
dt=0.01; %intervalo
tf=5; %tiempo final
x=0;
vX=0;
xx=zeros(1,tf/dt);
vv=zeros(1,tf/dt);
tipo=1; %inicialmente parada
xx(1)=0; %posición de la caja
vv(1)=0;
i=1;
for tt=0:dt:tf	
    t=t+dt;
    i=i+1;
	switch tipo 
        case 1  %parado
            y=y0+vY*t;
            fElastica=w*w*(y-x-d);
            if (fElastica>0) && (fElastica>muEst*9.8)
                t=0.0;
                y0=x0+muEst*9.8/w^2+d;
                vX=0;
                Ay=-(y0-x0-d-muDin*9.8/w^2);
                Ax=-vY/w;
                amplitud=sqrt(Ax^2+Ay^2);
                fase=atan2(Ay, Ax);
                if fase<0 
                    fase=2*pi+fase;
                end
                tipo=2;
             end
         case 2  %movimiento
            x=amplitud*sin(w*t+fase)+vY*t+y0-d-muDin*9.8/w^2;
            vX=amplitud*w*cos(w*t+fase)+vY;
            y=y0+vY*t;
            if vX<0
                vX=0;
                t=(4*pi-2*fase)/w;
                y=y0+vY*t;
                x=amplitud*sin(w*t+fase)+vY*t+y0-d-muDin*9.8/w^2;
                x0=x;
                y0=y;
                t=0;
                tipo=1;
            end 
         
    end
    xx(i)=x;
    vv(i)=vX;
end
figure
plot(xx, vv) %espacio de las fases posición-velocidad
grid on
xlabel('x')
ylabel('v_x')
title('Arrastrando una caja')
figure
plot(0:dt:tf, vv(1:end-1))  %gráfica tiempo-velocidad
grid on
xlabel('t')
ylabel('v_x')
title('Arrastrando una caja')
figure
plot(0:dt:tf, xx(1:end-1)) %gráfica tiempo-posición
grid on
xlabel('t')
ylabel('x')
title('Arrastrando una caja')

En la figura, se muestra la trayectoria de la caja en el espacio de fases x-v. Se observa las posiciones de la caja en reposo, en el eje horizontal. La velocidad de la caja aumenta, alcanza un máximo y luego, disminuye hasta que se detiene, comenzando un nuevo ciclo.

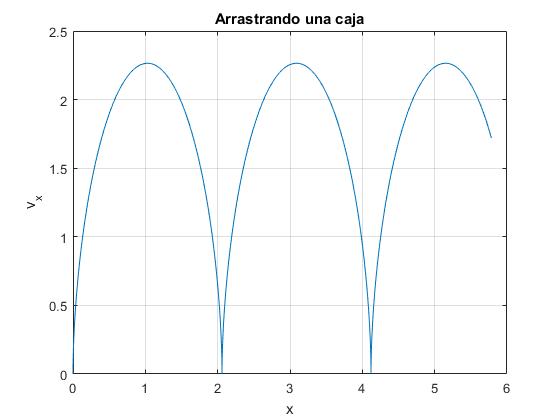
Datos v=1.0 m/s, k=10 N/m, M=1 kg, μ_s=0.75, μ_k=0.5

En la figura, se observa la velocidad de la caja en función del tiempo total t_t. Observamos que la velocidad de la caja aumenta, alcanza un máximo y luego, disminuye hasta que se detiene.

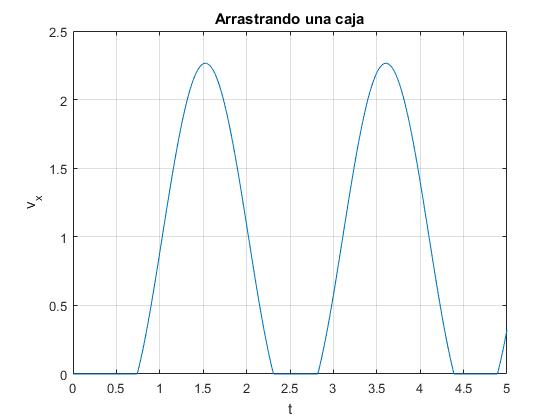
En la figura, se observa la posición de la caja en función del tiempo total t_t. Los segmentos horizontales indican que la caja permanece en reposo durante un determinado intervalo de tiempo.

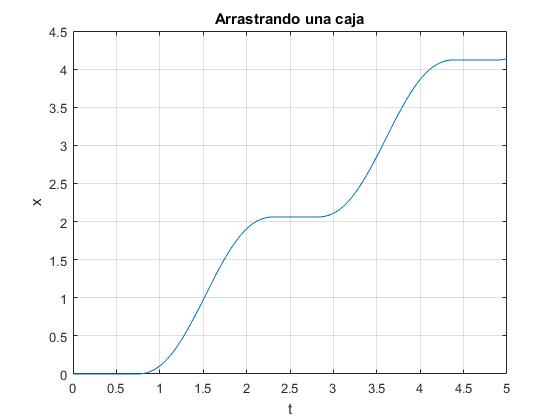
Actividades

Se introduce

• La velocidad constante v del operario, en m/s, en el control titulado Velocidad

• La masa M de la caja se ha fijado en 1 kg

• El coeficiente estático en el control titulado µ_s

• El coeficiente de rozamiento cinético en el control titulado µ_k. Se debe de cumplir que µ_k≤µ_s

• La constante k en N/m, del muelle elástico, en el control titulado Constante.

Se pulsa el botón titulado Nuevo

Se simula el movimiento de la caja y del operario, representado por un vehículo que se mueve con velocidad constante, ambos unidos por un muelle elástico.

En la parte superior, se representa la trayectoria de la caja en el espacio de las fases x-v. Se representan mediante flechas, las fuerzas sobre la caja