Choque de dos partículas iguales

Dos partículas iguales se mueven en la misma dirección y en sentido contrario con velocidad u. Después del choque su velocidad es v

Las velocidades de los cuerpos v₁=-v y v₂=v después del choque están relacionadas con las velocidades u₁=u y u₂=-u antes del choque mediante la definición del coeficiente de restitución e.

v₁-v₂=-e(u₁-u₂)
-2v=-e(2u), 

La velocidad v de los cuerpos después del choque disminuye ya que el coeficiente de restitución e<1.

v=e·u

Consideremos los cuerpos tienen una estructura interna, formada por dos partículas de masas m y M unidas por un muelle elástico de constante k y longitud l sin deformar.

La partícula de masa M del primer cuerpo choca elásticamente con la partícula de masa M del segundo cuerpo. Inmediatamente después del choque, dichas partículas cambian la dirección de su velocidad.

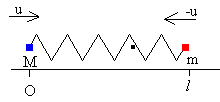
La situación inicial del sistema de partículas inmediatamente después del choque se muestra en la figura, la partícula de masa M se mueve hacia la derecha con velocidad u y la partícula de masa m se mueve hacia la izquierda con velocidad –u. Ambas partículas están separadas una distancia l, la longitud del muelle sin deformar.

Vamos a examinar el movimiento posterior de este sistema aislado: El centro de masas (c.m.) se mueve con velocidad constante. Las partículas se mueven bajo la acción de las fuerzas interiores o de interacción mutua.

Movimiento del centro de masas

La posición inicial y velocidad del c.m. son respectivamente

${\displaystyle z_0=\frac{ml}{M+m}{v}_{cm}=\frac{Mu+m(-u)}{m+M}=\frac{M-m}{m+M}u}$

En un sistema aislado el c.m. se mueve con velocidad constante

${\displaystyle z=\frac{ml}{M+m}+\left(\frac{M-m}{m+M}u\right)t}$

Como la velocidad inicial del c.m. es u antes del choque y la velocidad del c.m. después del choque es v=(M-m)u/(M+m) el coeficiente de restitución vale

${\displaystyle e=\left|\frac{v}{u}\right|=\left|\frac{M-m}{M+m}\right|=\left|\frac{1-\alpha }{1+\alpha }\right|\alpha =\frac{m}{M}}$

Movimiento relativo de las dos partículas

En un instante t la posición de la partícula de masa m (color rojo) es x y la posición de la partícula de masa M (color azul) es y.

La fuerza interna que actúa sobre cada una de las dos partículas es F=k(l-(x-y)). Donde (x-y) es la longitud del muelle deformado y l es la longitud del muelle sin deformar. Como no actúa ninguna fuerza exterior sobre el sistema de dos partículas, el sistema es aislado.

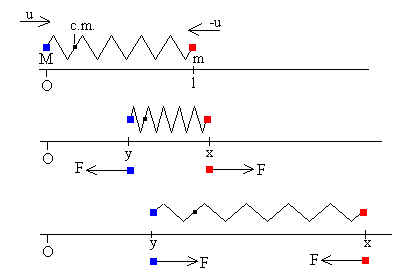
En la figura se muestra:

• En la parte superior, la situación inicial en el instante t=0.
• En la parte intermedia, cuando el muelle está comprimido. Como (x-y) es menor que l, la fuerza F es positiva para la partícula de la derecha (de masa m) y es negativa para la partícula de la izquierda (de masa M).
• En la parte inferior, cuando el muelle está estirado. Como (x-y) es mayor que l, la fuerza F es negativa para la partícula de la derecha (de masa m) y es positiva para la partícula de la izquierda (de masa M).

Las ecuaciones del movimiento son por tanto,

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=k\left(l-(x-y)\right)\\ M\frac{d^{2}y}{d{t}^2}=-k\left(l-(x-y)\right)\end{array}}$

Multiplicando la primera ecuación diferencial por M y la segunda por m y restando ambas ecuaciones diferenciales obtenemos.

${\displaystyle mM\left(\frac{d^{2}x}{d{t}^2}-\frac{d^{2}y}{d{t}^2}\right)=(m+M)k\left(l-(x-y)\right)}$

o bien,

${\displaystyle \frac{mM}{m+M}\frac{d^2\xi }{d{t}^2}=k(l-\xi )}$

donde ξ=x-y es la posición relativa de las dos partículas. Teniendo en cuenta la definición de masa reducida μ=mM/(m+M) del sistema formado por las dos partículas llegamos a la siguiente ecuación diferencial.

${\displaystyle \frac{d^2\xi }{d{t}^2}+\frac{k}{\mu }\xi =\frac{k}{\mu }l}$

La solución de esta ecuación diferencial, como puede comprobarse por simple sustitución es

${\displaystyle \begin{array}{l}\xi =l+A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\omega =\sqrt{\frac{k}{\mu }}=\sqrt{\frac{k(m+M)}{mM}}\\ \frac{d\xi }{dt}=A\omega \cos \left(\omega t\right)-B\omega \sin \left(\omega t\right)\end{array}}$

Las constantes A y B se determinan a partir de las condiciones iniciales.

${\displaystyle t=0\{\begin{array}{l}\xi =l+B\\ \frac{d\xi }{dt}=A\omega \end{array}}$

• la posición inicial de las partículas es x=l, y=0, por lo que ξ=x-y=l.
• la velocidad inicial de las partículas es dx/dt=-u, dy/dt=u, por lo que dξ/dt=-2u

${\displaystyle \xi =l-\frac{2u}{\omega }\sin \left(\omega t\right)}$

Conocemos la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=x-y de las partículas en función del tiempo t.

${\displaystyle \begin{array}{l}\frac{mx+My}{m+M}=\frac{ml}{M+m}+\left(\frac{M-m}{m+M}u\right)t\\ x-y=l-\frac{2u}{\omega }\sin \left(\omega t\right)\end{array}}$

Despejamos x e y de este sistema de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}x=l+\left(\frac{M-m}{M+m}u\right)t-\frac{M}{M+m}\frac{2u}{\omega }\sin (\omega t)\\ y=\left(\frac{M-m}{M+m}u\right)t+\frac{m}{M+m}\frac{2u}{\omega }\sin (\omega t)\end{array}}$

Comprobamos que en el instante t=0, las posiciones iniciales son x=l, y=0.

Las velocidades de las partículas en cualquier instante t son

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{M-m}{M+m}u-2u\frac{M}{M+m}\cos (\omega t)\\ \frac{dy}{dt}=\frac{M-m}{M+m}u+2u\frac{m}{M+m}\cos (\omega t)\end{array}}$

Energías del sistema de partículas

La energía inicial de las partículas es solamente cinética, el muelle está sin deformar

${\displaystyle U=\frac{1}{2}m{(-u)}^2+\frac{1}{2}M{u}^2=\frac{1}{2}(M+m)u^2}$

La energía del sistema de partículas en el instante t es

${\displaystyle E_k=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2=\frac{1}{2}\frac{{\left(M-m\right)}^2}{M+m}{u}^2+2u^2\frac{mM}{M+m}{\cos }^2(\omega t)}$

Teniendo en cuenta que la deformación del muelle es l-(x-y). La energía potencial de interacción entre las dos partículas es

${\displaystyle E_p=\frac{1}{2}k{\left(l-(x-y)\right)}^2=\frac{1}{2}k{\left(\frac{2u}{\omega }\right)}^2{\sin }^2(\omega t)=2u^2\frac{mM}{m+M}{\sin }^2(\omega t)}$

La energía total U del sistema de partículas es la suma de ambas contribuciones

${\displaystyle U=E_k+E_p=\frac{1}{2}(M+m)u^2}$

que es la energía inicial del sistema de partículas. En un sistema aislado la energía total U se mantiene constante.

Sucesivos choques

Los cuerpos volverán a chocar cuando la partícula de masa M regrese al origen, es decir, cuando y=0. El instante t₀ en el que ocurre, se obtiene resolviendo la ecuación transcendente

${\displaystyle \begin{array}{l}y=\left(\frac{M-m}{M+m}u\right)t+\frac{m}{M+m}\frac{2u}{\omega }\sin (\omega t)=0\\ \alpha =\frac{m}{M}\omega =\sqrt{\frac{k(m+M)}{mM}}=\sqrt{\frac{k}{M}}\sqrt{\frac{1+\alpha }{\alpha }}={\omega }_0\sqrt{\frac{1+\alpha }{\alpha }}\\ y=(1-\alpha )\left({\omega }_{0}t\sqrt{\frac{1+\alpha }{\alpha }}\right)+2\alpha \sin \left({\omega }_{0}t\sqrt{\frac{1+\alpha }{\alpha }}\right)\end{array}}$

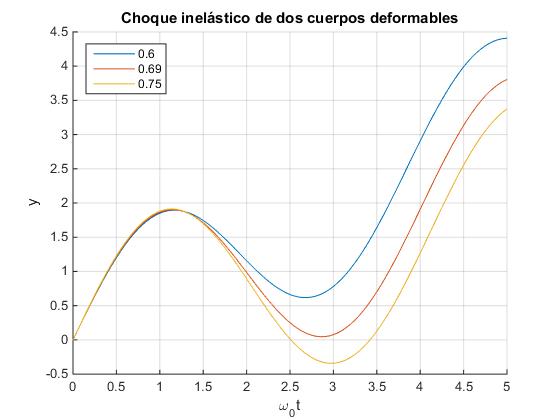
En la figura se representa y (eje vertical) en función de ω₀t (eje horizontal), para tres valores de α, 0.6, 0.69 y 0.75. Para el primer valor de α, la partícula .

wt=0:0.05:5;
hold on

for alfa=[0.6,0.69,0.75]
    y=(1-alfa)*wt*sqrt((1+alfa)/alfa)+2*alfa*sin(wt*sqrt((1+alfa)/alfa));
    plot(wt,y, 'displayName',num2str(alfa))
end
hold off
grid on
legend('-DynamicLegend','location','northwest')

xlabel('\omega_0t')
ylabel('y')
title('Choque inelástico de dos cuerpos deformables')

El valor crítico de α_c, se obtiene haciendo iguales a cero, la función y su derivada.

${\displaystyle \{\begin{array}{l}y=0\\ \frac{dy}{d({\omega }_{0}t)}=0\end{array}}$

Eliminando ω₀t  en el sistema de dos ecuaciones llegamos a la ecuación trascendente en α.

${\displaystyle (1-\alpha )\left(\pi +\arccos \left(\frac{1-\alpha }{2\alpha }\right)\right)-\sqrt{3{\alpha }^2+2\alpha -1}=0}$

>> f=@(x) (1-x)*(pi+acos((1-x)/(2*x)))-sqrt(3*x^2+2*x-1);
>> fplot(f,[0,1])
>> grid on
>> fzero(f,[0.6,0.8])
ans =    0.6971

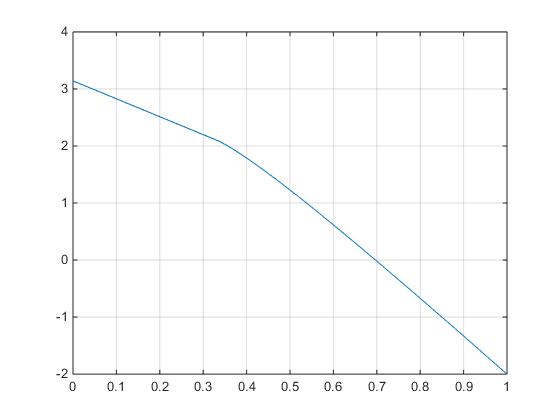
La raíz es α_c=0.6971

• Cuando α< α_c solamente se produce un choque entre las partículas de masa M de cada uno de los cuerpos.
• Cuando α>α_c se produce más de un choque entre las partículas de masa M de cada uno de los cuerpos.

En dicho instante la posición de las partículas es

${\displaystyle \begin{array}{l}{x}_0=l+\left(\frac{M-m}{M+m}u\right)t_0-\frac{M}{M+m}\frac{2u}{\omega }\sin (\omega t_0)\\ y_0=0\end{array}}$

La partícula de masa M (color azul) choca elásticamente con la correspondiente del otro cuerpo y cambia el signo de dicha velocidad.

${\displaystyle \begin{array}{l}{v}_{0x}=\frac{M-m}{M+m}u-2u\frac{M}{M+m}\cos (\omega t_0)\\ v_{0y}=-\left(\frac{M-m}{M+m}u+2u\frac{m}{M+m}\cos (\omega t_0)\right)\end{array}}$

Tenemos que estudiar la dinámica del sistema de dos partículas con las condiciones iniciales especificadas para el instante t₀.

Movimiento del centro de masas

La posición inicial y velocidad del c.m. son respectivamente

${\displaystyle z_0=\frac{m{x}_0}{M+m}{v}_{cm}=\frac{M{v}_{0y}+m{v}_{0x}}{m+M}}$

En un sistema aislado el c.m. se mueve con velocidad constante

${\displaystyle z=\frac{m{x}_0}{M+m}+\frac{M{v}_{0y}+m{v}_{0x}}{m+M}t}$

Movimiento de las partículas

La ecuación del movimiento relativo de las dos partículas la hemos deducido en la sección anterior. Su solución es

${\displaystyle \begin{array}{l}\xi =l+A\sin \left(\omega t\right)+B\cos \left(\omega t\right)\omega =\sqrt{\frac{k}{\mu }}=\sqrt{\frac{k(m+M)}{mM}}\\ \frac{d\xi }{dt}=A\omega \cos \left(\omega t\right)-B\omega \sin \left(\omega t\right)\end{array}}$

Las constantes A y B se determinan a partir de las condiciones iniciales, que en este caso son diferentes.

${\displaystyle t=t_0\{\begin{array}{l}\xi =l+A\sin (\omega t_0)+B\cos (\omega t_0)\\ \frac{d\xi }{dt}=A\omega \cos (\omega t_0)-B\omega \sin (\omega t_0)\end{array}}$

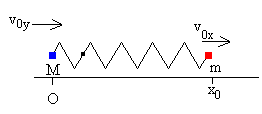
• la posición de las partículas es x=x₀, y=0, por lo que ξ=x-y=x₀.

• la velocidad inicial de las partículas es dx/dt=v_0x, dy/dt=v_0y, por lo que dξ/dt= v_0x-v_0y.

$$\begin{gathered} {\displaystyle \begin{array}{l}\xi =l+\left((x_0-l)\sin (\omega t_0)+\frac{v_{0x}-v_{0y}}{\omega }\cos (\omega t_0)\right)\sin \left(\omega t\right)+ \\ \left((x_0-l)\cos (\omega t_0)-\frac{v_{0x}-v_{0y}}{\omega }\sin (\omega t_0)\right)\cos \left(\omega t\right)\\ \frac{d\xi }{dt}=\left((x_0-l)\sin (\omega t_0)+\frac{v_{0x}-v_{0y}}{\omega }\cos (\omega t_0)\right)\omega \cos \left(\omega t\right)- \\ \left((x_0-l)\cos (\omega t_0)-\frac{v_{0x}-v_{0y}}{\omega }\sin (\omega t_0)\right)\omega \sin \left(\omega t\right)\end{array}} \end{gathered}$$

Conocemos la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=x-y de las partículas en función del tiempo t. Despejamos x e y de este sistema de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}x=z+\frac{M}{M+m}\xi \\ y=z-\frac{m}{M+m}\xi \end{array}}$

Estas son las ecuaciones generales del movimiento del sistema de dos partículas después del choque. Las ecuaciones de la primera sección se deducen poniendo t₀=0, x₀=l, v_0x=-u, v_0y=u.

El instante en el que tiene lugar el próximo choque, si es que existe se obtiene resolviendo la ecuación trascendente y=0.

Actividades

Se introduce:

• El cociente m/M de las masas de las partículas, m es la masa de la partícula de color rojo y M la masa de la partícula de color azul, en el control titulado Cociente m/M
• La constante k del muelle elástico, en el control titulado Constante muelle.
• La longitud l del muelle sin deformar se ha fijado en 0.25 m.
• La velocidad inicial de las dos partículas se ha fijado en -1.0.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del sistema formado por dos partículas unidas por un muelle elástico. En la parte superior, observamos que la energía del sistema de partículas suma de:

• La energía cinética de la primera partícula (de color azul)
• La energía cinética de la segunda partícula (de color rojo)
• La energía potencial elástica del muelle deformado (color gris)

Referencias

Aguirregabiria J. M., Hernández A., Rivas M. A simple model for inelastic collisions. Am. J. Phys. 76 (11) November 2008, pp. 1071-1073.