El péndulo simple

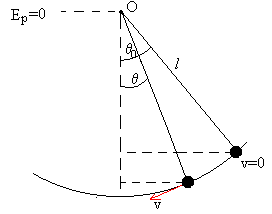
Supongamos que un péndulo simple de masa m y de longitud l se desvía un ángulo θ₀ de la posición de equilibrio y se suelta.

Principio de conservación de la energía

Aplicamos el principio de conservación de la energía para calcular la velocidad de la partícula cuando el péndulo se encuentra en la posición angular θ.

Establecemos el nivel cero de energía potencial en el eje de giro O

${\displaystyle \frac{1}{2}m{v}^2-mgl\cos \theta =-mgl\cos {\theta }_0}$

Como la partícula describe un movimiento circular de radio l, la velocidad v=l(dθ/dt).

${\displaystyle {\left(\frac{d\theta }{dt}\right)}^2=\frac{2g}{l}(\cos \theta -\cos {\theta }_0)}$

Segunda ley de Newton

En la figura, se muestran las fuerzas que actúan sobre la partícula de masa m y las componentes tangencial a_t= l(d²θ/dt²) y normal a_n=v²/l =l(dθ/dt)² de su aceleración.

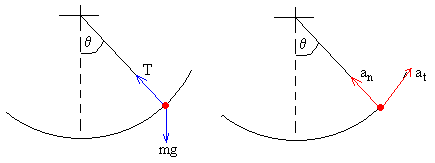
Aplicamos la segunda ley de Newton

ma_t=-mg·sinθ
ma_n=T-mg·cosθ

La primera ecuación se escribe en forma diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta =0}$

Se resuelve esta ecuación diferencial de segundo orden por procedimientos numéricos, con las condiciones iniciales t=0, θ=θ₀, (dθ/dt)=0

La segunda ecuación, nos permite calcular la tensión de la cuerda T conocida la velocidad v de la partícula. La velocidad v se calcula aplicando el principio de conservación de la energía

${\displaystyle \frac{T}{mg}=3\cos \theta -2\cos {\theta }_0}$

El péndulo situado sobre una plataforma móvil que desliza sobre un plano horizontal

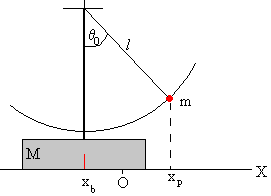
La plataforma y el péndulo constituyen un sistema aislado. Supongamos que inicialmente el péndulo se encuentra en la posición de equilibrio, en reposo, encima del centro de masas del la plataforma. Su proyección sobre el eje horizontal X señala el origen O. Así pues, el origen O es la posición del centro de masas del sistema aislado que permanecerá en reposo si inicialmente lo estaba.

La posición del centro de masas del sistema es el origen X_c=0

Supongamos que el péndulo se desplaza de la posición de equilibrio un ángulo θ₀ hacia la derecha.

• La posición del c.m. de la plataforma es x_b.

• La posición de la partícula es x_p=-x_b+l·sinθ.

• La posición del centro de masas es X_c=0

${\displaystyle 0=\frac{m{x}_p+M·x_b}{m+M}}$

La relación entre la posición angular θ del péndulo y la posición del c.m. de la plataforma x_b es

${\displaystyle x_b=-\frac{m}{m+M}l·\sin \theta }$

La velocidad del centro de masas del sistema es V_c=0

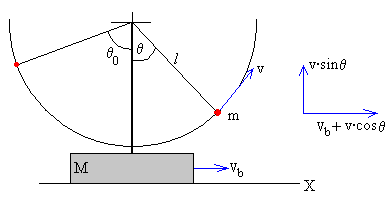
Las componentes de la velocidad de la partícula, respecto del observador inercial situado en el plano horizontal, son

horizontal: vcosθ+V_b
vertical: v·sinθ

${\displaystyle 0=\frac{m(v\cos \theta +V_b)+M{V}_b}{m+M}}$

La relación entre la velocidad v de la partícula y la velocidad V_b de la plataforma es

${\displaystyle V_b=-\frac{m}{m+M}v\cos \theta }$

Se obtiene derivando la relación entre la posición angular θ del péndulo y la posición del c.m. de la plataforma x_b

Principio de conservación de la energía

Si establecemos el nivel cero de energía potencial en el eje de giro del péndulo. El principio de conservación de la energía se escribe, véase figura anterior.

${\displaystyle \frac{1}{2}M{V}_b^2+\frac{1}{2}m\left({(v\cos \theta +V_b)}^2+{(v·\sin \theta )}^2\right)-mgl\cos \theta =-mgl\cos {\theta }_0}$

Sustituimos V_b en función de v y despejamos v=l(dθ/dt)

${\displaystyle {\left(\frac{d\theta }{dt}\right)}^2=\frac{2g}{l}(\cos \theta -\cos {\theta }_0)\frac{M+m}{M+m{\sin }^2\theta }}$

La aceleración del centro de masas del sistema es a_c=0

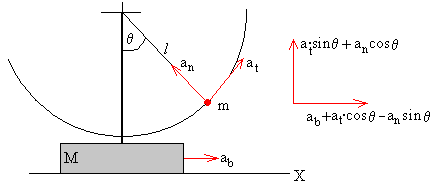
Las componentes horizontal y vertical de la aceleración de la partícula, respecto del observador inercial situado en el plano horizontal, son

a_tcosθ-a_nsinθ+a_b
a_ncosθ+a_tsinθ

${\displaystyle 0=\frac{m(a_t\cos \theta -a_n\sin \theta +a_b)+M{a}_b}{m+M}}$

La relación entre las componentes tangencial a_t y normal a_n de la aceleración de la partícula y la aceleración a_b de la plataforma es

${\displaystyle a_b=-\frac{m}{m+M}(a_t\cos \theta -a_n\sin \theta )}$

Segunda ley de Newton

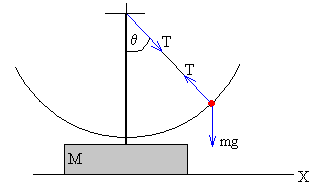
Las fuerzas sobre la partícula son

• La tensión T
• El peso mg

• La tensión T de la cuerda
• El peso de la plataforma y la reacción del plano horizontal no contribuyen al movimiento

Las componentes tangencial y radial de la aceleración de la partícula, respecto del observador inercial situado en el plano horizontal, son

a_t+a_b·cosθ
a_n-a_b·sinθ

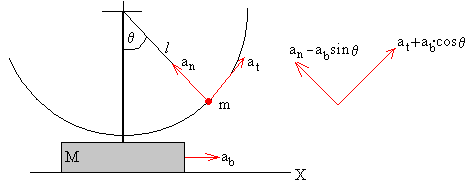
La ecuación del movimiento en la dirección tangencial es

m(a_t+a_b·cosθ)=-mgsinθ

La ecuación del movimiento en la dirección normal es

m(a_n-a_b·sinθ)=T- mgcosθ

La ecuación del movimiento de la plataforma es

T·sinθ=Ma_b

Sustituimos a_b y teniendo en cuenta que a_n=l(dθ/dt)² y a_t= l(d²θ/dt²)  llegamos a la siguiente ecuación diferencial de segundo orden

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{m}{M+m{\sin }^2\theta }\sin \theta ·\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{l}\frac{M+m}{M+m{\sin }^2\theta }\sin \theta =0}$

Que se resuelve por procedimientos numéricos con las siguientes condiciones iniciales

t=0, θ=θ₀, (dθ/dt)=0

Cuando la masa M de la plataforma es muy grande comparada con la masa m de la partícula, m/M→0 obtenemos la ecuación diferencial del movimiento del péndulo.

Vamos a comprobar si es correcta la ecuación diferencial del movimiento.

La aplicación del principio de conservación de la energía nos proporciona la ecuación diferencial de primer orden

${\displaystyle {\left(\frac{d\theta }{dt}\right)}^2=\frac{2g}{l}(\cos \theta -\cos {\theta }_0)\frac{M+m}{M+m{\sin }^2\theta }}$

Derivamos esta ecuación respecto del tiempo

${\displaystyle \begin{array}{l}2\left(\frac{d\theta }{dt}\right)\frac{d^2\theta }{d{t}^2}=\frac{2g}{l}(-\sin \theta )\frac{M+m}{M+m{\sin }^2\theta }\left(\frac{d\theta }{dt}\right)+\frac{2g}{l}(\cos \theta -\cos {\theta }_0)\frac{(-2m\sin \theta ·\cos \theta )(M+m)}{{(M+m{\sin }^2\theta )}^2}\left(\frac{d\theta }{dt}\right)\\ \frac{d^2\theta }{d{t}^2}=\frac{g}{l}(-\sin \theta )\frac{M+m}{M+m{\sin }^2\theta }+\frac{2g}{l}(\cos \theta -\cos {\theta }_0)\frac{(-m\sin \theta ·\cos \theta )(M+m)}{{(M+m{\sin }^2\theta )}^2}\\ \frac{d^2\theta }{d{t}^2}=\frac{g}{l}(-\sin \theta )\frac{M+m}{M+m{\sin }^2\theta }+{\left(\frac{d\theta }{dt}\right)}^2\frac{M+m{\sin }^2\theta }{(M+m)}\frac{(-m\sin \theta ·\cos \theta )(M+m)}{{(M+m{\sin }^2\theta )}^2}\\ \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\frac{M+m}{M+m{\sin }^2\theta }\sin \theta +{\left(\frac{d\theta }{dt}\right)}^2\frac{m\sin \theta ·\cos \theta }{M+m{\sin }^2\theta }=0\end{array}}$

y volvemos a obtener la ecuación diferencial del movimiento

Tensión de la cuerda

Despejamos la tensión de la cuerda

${\displaystyle T\frac{M+m{\sin }^2\theta }{M}=ml{\left(\frac{d\theta }{dt}\right)}^2+mg\cos \theta }$

Conocida la velocidad angular de rotación (dθ/dt), obtenemos T

${\displaystyle \frac{T}{mg}=\frac{M}{{\left(M+m{\sin }^2\theta \right)}^2}\left(3(M+m)\cos \theta -m{\cos }^3\theta -2(M+m)\cos {\theta }_0\right)}$

Ejemplo: supongamos que el péndulo se desvía θ₀=90º y se suelta. Cuando pasa por la posición de equilibrio θ=0, la tensión de la cuerda es

${\displaystyle \frac{T}{mg}=3+2\frac{m}{M}}$

Algo mayor que cuando la plataforma está fija T/(mg)=3

Cuando la masa M de la plataforma es muy grande comparada con la masa m de la partícula, m/M→0 obtenemos

${\displaystyle \frac{T}{mg}=3\cos \theta -2\cos {\theta }_0}$

Ejemplo

• Masa de la plataforma M=2 kg, masa de la partícula m=1 kg, de modo que el cociente M/m=2.0
• Longitud del péndulo, l=1.0 m
• Ángulo inicial de desviación del péndulo θ₀=90º

El bloque se desvía hacia la izquierda, a fin de que la posición del c.m. del sistema aislado permanezca en el origen

${\displaystyle x_b=-\frac{m}{m+M}l·\sin \theta x_b=-\frac{1}{1+2}1.0·\text{sin 90}=\frac{\text{1}}{\text{3}}\text{m}}$

Calcular la posición x_b del bloque, la velocidad v de la partícula, la velocidad V_b de la plataforma y la tensión T de la cuerda cuando θ=30º

${\displaystyle x_b=-\frac{1}{1+2}1.0·\sin \text{30}=\frac{\text{1}}{\text{6}}\text{m}}$

La conservación del momento lineal y de la energía nos proporcionan las dos ecuaciones que nos permiten calcular v y V_b.

${\displaystyle \begin{array}{l}m(v\cos \theta +V_b)+M{V}_b=0\\ \frac{1}{2}M{V}_b^2+\frac{1}{2}m\left({(v\cos \theta +V_b)}^2+{(v·\sin \theta )}^2\right)-mgl\cos \theta =-mgl\cos {\theta }_0\\ 1(v\cos 30º+V_b)+2V_b=0\\ \frac{1}{2}2V_b^2+\frac{1}{2}1\left({(v\cos \theta +V_b)}^2+{(v·\sin \theta )}^2\right)-1·9.8·1.0\cos 30º=-1·9.8·1.0\cos 90º\end{array}}$

v=-4.75 m/s, V_b=1.37 m/s

La tensión T de la cuerda se calcula mediante el par de ecuaciones

T·sinθ=Ma_b
m(a_n-a_b·sinθ)=T- mgcosθ

T·sin30º=2·a_b
1(4.75²/1.0-a_b·sin30º)=T- 1·9.8·cos30º

Eliminando la aceleración a_b de la plataforma, despejamos T=27.66 N

Comparación

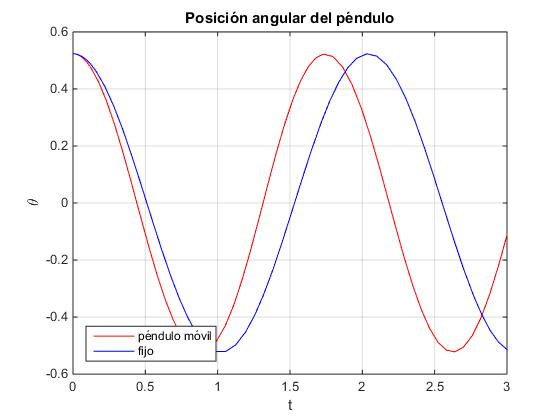
La figura muestra, la comparación entre las oscilaciones de un péndulo (en color azul) y la del mismo péndulo montado en una plataforma móvil (en color rojo) cuya masa es M/m=2. El péndulo se suelta desde la posición θ₀=π/6 (30°)

M=2; %relación M/m (plataforma/péndulo)
w2=9.8/1.0; %cuadrado de la frecuencia angular del péndulo simple

%péndulo móvil
f=@(t,x) [x(2);-(w2*(M+1)*sin(x(1))+sin(2*x(1))*x(2)/2)/(M+sin(x(1))^2)]; 
tspan=[0 3];
[t,x]=ode45(f,[0,3],[pi/6,0]);

%péndulo fijo
g=@(t,x) [x(2);-w2*sin(x(1))]; 
[tt,xx]=ode45(g,[0,3],[pi/6,0]);

plot(t,x(:,1),'r',tt,xx(:,1),'b')
legend('péndulo móvil','fijo', 'location','southwest')
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular del péndulo')

figure 
y=-sin(x(:,1))/(1+M);
plot(t,y,'r')
grid on
xlabel('t')
ylabel('x');
title('Posición de la plataforma')

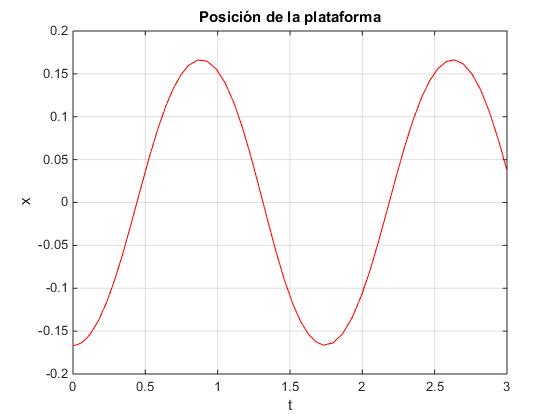
La figura muestra la posición de la plataforma x_b en función del tiempo.

Actividades

Se introduce

• El ángulo inicial θ₀,, en el control titulado Desviación
• El cociente masa de la plataforma, masa de la partícula M/m, en el control titulado Cociente M/m
• La longitud del péndulo se ha fijado en l=1 m.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del péndulo y de la plataforma

En la parte superior, se proporcionan los datos relativos al tiempo t y:

• al péndulo: ángulo de desviación θ, velocidad angular dθ/dt y tensión T de la cuerda.
• a la plataforma: posición x_b y velocidad V_b

Ecuaciones de Lagrange

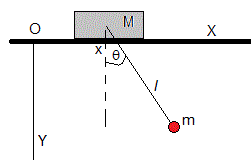
• La posición de la plataforma móvil de masa M es x
• La posición de la masa puntual m es (x+lsinθ, lcosθ)

Si el centro de masas está situado el origen, relacionamos la posición de la plataforma x con el ángulo de desviación del péndulo θ,

m(x+lsinθ)+Mx=0

Derivando respecto al tiempo, obtenemos la velocidad de la plataforma y su energía cinética T₁

${\displaystyle \begin{array}{l}x=-\frac{ml\sin \theta }{m+M}\\ v=\frac{dx}{dt}=-\frac{ml\cos \theta }{m+M}\frac{d\theta }{dt}\\ T_1=\frac{1}{2}M{\left(\frac{ml\cos \theta }{m+M}\right)}^2{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

y de la masa puntual m y su energía cinética T₂

${\displaystyle \begin{array}{l}{v}_x=\frac{dx}{dt}+l\cos \theta \frac{d\theta }{dt}=-\frac{ml\cos \theta }{m+M}\frac{d\theta }{dt}+l\cos \theta \frac{d\theta }{dt}=\frac{M}{m+M}l\cos \theta \frac{d\theta }{dt}\\ v_y=l\sin \theta \frac{d\theta }{dt}\\ T_2=\frac{1}{2}m\left({\left(\frac{M}{m+M}\cos \theta \right)}^2+{\sin }^2\theta \right)l^2{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

La energía potencial de la masa puntual es

${\displaystyle V=mgl\left(1-\cos \theta \right)}$

La lagrangiana L=T₁+T₂-V es

${\displaystyle L=\frac{1}{2}\frac{mM}{m+M}{l}^2{\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}m{l}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2-mgl\left(1-\cos \theta \right)}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{\partial L}{\partial \dot{\theta }}=\frac{mM}{m+M}{l}^2{\cos }^2\theta \dot{\theta }+m{l}^2{\sin }^2\theta \dot{\theta }\\ \frac{\partial }{\partial t}\left(\frac{\partial L}{\partial \dot{\theta }}\right)=m\left(\frac{M+m{\sin }^2\theta }{m+M}\right)l^2\ddot{\theta }+2\left(\frac{m^2}{m+M}\right)l^2\cos \theta \sin \theta {\dot{\theta }}^2\\ \frac{\partial L}{\partial \theta }=-\frac{mM}{m+M}{l}^2\cos \theta \sin \theta {\dot{\theta }}^2+m{l}^2\cos \theta \sin \theta {\dot{\theta }}^2-mgl\sin \theta \\ \left(\frac{M+m{\sin }^2\theta }{m+M}\right)\frac{d^2\theta }{d{t}^2}+\frac{m}{m+M}\cos \theta \sin \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{l}\sin \theta =0\end{array}}$

Obtenemos la misma ecuación que en los apartados anteriores

Oscilaciones de pequeña amplitud

Cuando el ángulo θ es pequeño, la lagrangiana L y la ecuación del movimiento se simplifican notablemente

${\displaystyle \begin{array}{l}L=\frac{1}{2}\frac{mM}{m+M}{l}^2{\left(\frac{d\theta }{dt}\right)}^2-\frac{1}{2}mgl{\theta }^2\\ \frac{\partial }{\partial t}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{M}{m+M}\frac{d^2\theta }{d{t}^2}+\frac{g}{l}\theta =0\end{array}}$

Se trata de la ecuación diferencial de un Movimiento Armónico Simple de frecuencia angular

${\displaystyle {\omega }^2=\frac{g}{l}\left(1+\frac{m}{M}\right)}$

Si la masa M de la plataforma móvil es muy grande, obtenemos la frecuencia angular ω del movimiento oscilatorio de un péndulo de longitud l

El péndulo situado sobre una plataforma móvil que desliza sobre un plano inclinado

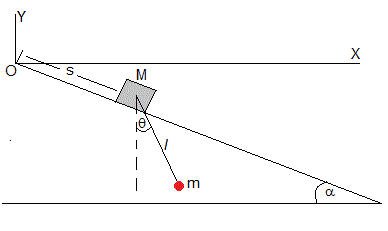
Una plataforma de masa M desliza sin rozamiento a lo largo de un plano inclinado de ángulo α. El cuerpo está unido a una partícula de masa m mediante un hilo inextensible y de masa despreciable de longitud l. Se separa el hilo de la posición vertical y se suelta y a la vez se libera la plataforma. Se trata de describir el movimiento de la plataforma a lo largo del plano inclinado y el movimiento del péndulo respecto de dicho cuerpo.

La posición de la plataforma y de la partícula en el instante t

${\displaystyle M\{\begin{array}{l}{x}_M=s·\cos \alpha \\ y_M=-s·\sin \alpha \end{array}m\{\begin{array}{l}{x}_m=s·\cos \alpha +l\sin \theta \\ y_m=-s·\sin \alpha -l\cos \theta \end{array}}$

Las componentes de la velocidad son

${\displaystyle M\{\begin{array}{l}\frac{d{x}_M}{dt}=\frac{ds}{dt}\cos \alpha \\ \frac{d{y}_M}{dt}=-\frac{ds}{dt}\sin \alpha \end{array}m\{\begin{array}{l}\frac{d{x}_m}{dt}=\frac{ds}{dt}\cos \alpha +\frac{d\theta }{dt}l\cos \theta \\ \frac{d{y}_m}{dt}=-\frac{ds}{dt}\sin \alpha +\frac{d\theta }{dt}l\sin \theta \end{array}}$

La energía cinética del sistema es

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}M\left\{{\left(\frac{d{x}_M}{dt}\right)}^2+{\left(\frac{d{y}_M}{dt}\right)}^2\right\}+\frac{1}{2}m\left\{{\left(\frac{d{x}_m}{dt}\right)}^2+{\left(\frac{d{y}_m}{dt}\right)}^2\right\}=\\ =\frac{1}{2}M{\left(\frac{ds}{dt}\right)}^2+\frac{1}{2}m\left\{{\left(\frac{ds}{dt}\right)}^2+l^2{\left(\frac{d\theta }{dt}\right)}^2+2l\frac{ds}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )\right\}=\\ \frac{1}{2}(M+m){\left(\frac{ds}{dt}\right)}^2+\frac{1}{2}m\left\{l^2{\left(\frac{d\theta }{dt}\right)}^2+2l\frac{ds}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )\right\}\end{array}}$

La energía potencial del sistema tomando el origen como nivel cero es

${\displaystyle E_p=-Mgs·\sin \alpha -mg(s·\sin \alpha +l\cos \theta )}$

La lagrangiana L=E_k-E_p y las ecuaciones del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{s}}\right)-\frac{\partial L}{\partial s}=0\\ \frac{d}{dt}\left((m+M)\frac{ds}{dt}+ml\frac{d\theta }{dt}\cos (\alpha +\theta )\right)-Mg\sin \alpha -mg\sin \alpha =0\\ (m+M)\frac{d^{2}s}{d{t}^2}+ml\left(\frac{d^2\theta }{d{t}^2}\cos (\alpha +\theta )-{\left(\frac{d\theta }{dt}\right)}^2\sin (\alpha +\theta )\right)-(m+M)g\sin \alpha =0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(m{l}^2\frac{d\theta }{dt}+ml\frac{ds}{dt}\cos (\alpha +\theta )\right)+ml\frac{ds}{dt}\frac{d\theta }{dt}\sin (\alpha +\theta )+mgl\sin \theta =0\\ l\frac{d^2\theta }{d{t}^2}+\frac{d^{2}s}{d{t}^2}\cos (\alpha +\theta )+g\sin \theta =0\end{array}}$

Tenemos un sistema de dos ecuaciones diferenciales, despejamos d²s/dt² y d²θ/dt²

${\displaystyle \begin{array}{l}\left(M+m{\sin }^2(\alpha +\theta )\right)\frac{1}{l}\frac{d^{2}s}{d{t}^2}-m{\left(\frac{d\theta }{dt}\right)}^2\sin (\alpha +\theta )-\frac{g}{l}\left\{m\sin \theta \cos (\alpha +\theta )+(m+M)\sin \alpha \right\}=0\\ \left(M+m{\sin }^2(\alpha +\theta )\right)\frac{d^2\theta }{d{t}^2}+m{\left(\frac{d\theta }{dt}\right)}^2\sin (\alpha +\theta )\cos (\alpha +\theta )+\left(M+m\right)\frac{g}{l}\left\{\sin \theta +\sin \alpha \cos (\alpha +\theta )\right\}=0\end{array}}$

Cuando el plano es horizontal, α=0

${\displaystyle \begin{array}{l}\frac{1}{l}\frac{d^{2}s}{d{t}^2}-\frac{m}{M+m{\sin }^2\theta }{\left(\frac{d\theta }{dt}\right)}^2\sin \theta -\frac{m}{M+m{\sin }^2\theta }\frac{g}{l}\sin \theta \cos \theta =0\\ \frac{d^2\theta }{d{t}^2}+\frac{m\sin \theta \cos \theta }{M+m{\sin }^2\theta }{\left(\frac{d\theta }{dt}\right)}^2+\frac{M+m}{M+m{\sin }^2\theta }\frac{g}{l}\sin \theta =0\end{array}}$

La segunda ecuación diferencial coincide con el apartado anterior. Verificamos la primera a partir de la relación entre s o x_b y el ángulo θ

${\displaystyle x_b=-\frac{m}{m+M}l·\sin \theta }$

derivando dos veces con respecto del tiempo

Ejemplo

• Masa de la plataforma M=0.5 kg, masa de la partícula m=1 kg, de modo que el cociente M/m=0.5
• Longitud del péndulo, l=0.3 m
• Ángulo inicial de desviación del péndulo θ₀=-π/3 (-60º)
• Ángulo del plano inclinado, α=5°

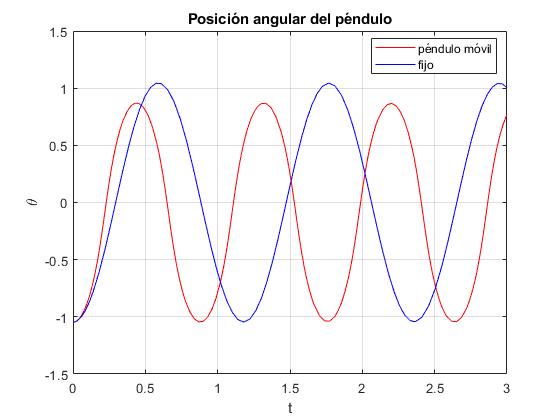
Representamos la posición angular θ del péndulo móvil en función del tiempo y lo comparamos con la posición angular de un péndulo fijo similar. Representamos la posición de la plataforma s a lo largo del plano inclinado

M=0.5; %relación M/m
l=0.3; %longitud del péndulo
w2=9.8/l; %es el cuadrado de la frecuencia angular del péndulo simple
alfa=5*pi/180; %ángulo del plano inclinado
%s es x(1) ds/dt es x(2), th es x(3), dth/dt es x(4)
f=@(t,x) [x(2); l*(x(4)^2*sin(alfa+x(3))+w2*(sin(x(3))*cos(alfa+x(3))
+(1+M)*sin(alfa)))/(M+sin(alfa+x(3))^2); x(4); 
-(x(4)^2*sin(alfa+x(3))*cos(alfa+x(3))+(1+M)*w2*(sin(x(3))+sin(alfa)*
cos(alfa+x(3))))/(M+sin(alfa+x(3))^2)]; 
[t,x]=ode45(f,[0,3],[0,0,-pi/3,0]);
%péndulo fijo
g=@(t,x) [x(2);-w2*sin(x(1))]; 
[tt,xx]=ode45(g,[0,3],[-pi/3,0]);

plot(t,x(:,3),'r',tt,xx(:,1),'b')
legend('péndulo móvil','fijo', 'location','best')
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular del péndulo')

figure 
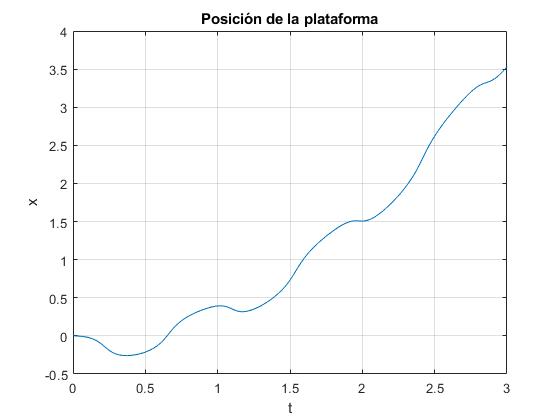
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Posición de la plataforma')

Verificamos la conservación de la energía

${\displaystyle E=\frac{1}{2}(M+m){\left(\frac{ds}{dt}\right)}^2+\frac{1}{2}m\left\{l^2{\left(\frac{d\theta }{dt}\right)}^2+2l\frac{ds}{dt}\frac{d\theta }{dt}\cos (\alpha +\theta )\right\}-(M+m)gs·\sin \alpha -mgl\cos \theta }$

La energía inicial cuando la plataforma se encuentra en reposo en el origen s=0 y el péndulo se ha desviado θ₀ de la dirección vertical

E₀=-mglcosθ₀

>> E=(1+M)*x(:,2).^2/2+(l^2*x(:,4).^2+2*l*x(:,2).*x(:,4).*cos(alfa+x(:,3)))/2-
(1+M)*9.8*x(:,1)*sin(alfa)-9.8*l*cos(x(:,3))

    -1.4700
    -1.4700
  ....
    -1.4661
    -1.4661
    >> -9.8*l*cos(-pi/3)
ans =   -1.4700

Actividades

Se introduce

• El ángulo del plano inclinado α, en el control titulado ¨Ángulo
• El ángulo inicial θ₀,, en el control titulado Desviación
• El cociente masa de la plataforma, masa de la partícula M/m, en el control titulado Cociente M/m
• La longitud del péndulo se ha fijado en l=0.3 m.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del péndulo y de la plataforma

En la parte superior, se proporcionan los datos relativos al tiempo t y

• al péndulo: ángulo de desviación θ, velocidad angular dθ/dt
• a la plataforma: posición s, y velocidad ds/dt

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte inferior izquierda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Referencias

Physics challenges for teachers and students (Solutions to November 2004), The Physics Teacher 43 (2005), pp. s2-s3.

David Morin. Chapter 5. The Lagrangian Method. 2002