Movimiento del c.m. y de las partículas de un sistema (III)
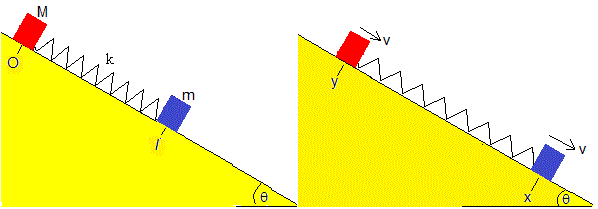
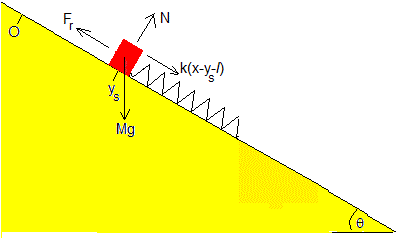
Un bloque de masa M (en color rojo) unido mediante un muelle elástico de constante k y longitud l sin deformar, a un carrito (en color azul) de masa m situados ambos sobre un plano inclinado de ángulo θ. El coeficiente de rozamiento (estático y cinético) entre el bloque y el plano inclinado es μ. Supondremos que no hay rozamiento apreciable entre el carrito y el plano inclinado.
Descripción del movimiento
El comportamiento del bloque depende de los valores de los parámetros mencionados, como veremos más adelante:
- Permanecerá en reposo en el origen
- Deslizará a lo largo del plano inclinado, deteniéndose y volviendo a deslizar hasta alcanzar la posición final en reposo
- Deslizará a lo largo del plano inclinado sin detenerse
El bloque de masa M se encuentra inicialmente en el origen en reposo y el carrito se sostiene a una distancia l igual a la longitud del muelle si deformar.
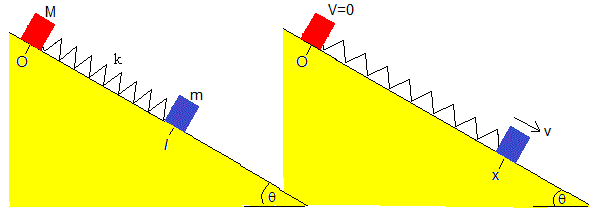
Se suelta el carrito, en el instante t=0, se desplaza (x-l) y adquiere una velocidad v. Aplicamos el principio de conservación de la energía
El máximo desplazamiento del carrito xm se obtiene cuando se detiene v=0
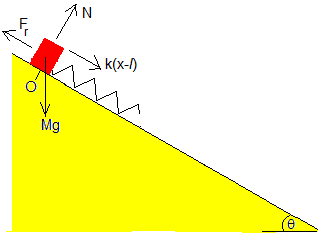
La fuerza de rozamiento que hace que el bloque permanezca en reposo sobre el plano inclinado es Fr=k(x-l)+Mgsinθ.
Fr aumenta con la deformación (x-l). Cuando esta fuerza alcanza el valor máximo Fr=μN=μMgcosθ el bloque empieza a deslizar.
El bloque permanecerá en reposo en el origen mientras el carrito oscila siempre que
La masa mínima m1 que hace que el bloque empiece a deslizar se obtiene de las ecuaciones
Siempre que m<m1, el bloque permanece en reposo en el origen y el carrito oscilará a lo largo del plano inclinado.
Si (m+M)gsinθ>μMgcosθ, el bloque no se detiene, acelera
Siempre que m>m2, el bloque deslizará a lo largo del plano inclinado sin detenerse.
El principal interés de este página radica en carritos de masa m comprendida entre m1 y m2.
Tomaremos un coeficiente de rozamiento μ de modo que m1 y m2 sean positivas, lo que implica μ>tanθ
El bloque en reposo, el carrito se mueve
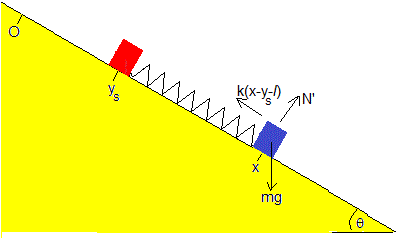
El bloque se encuentra en reposo en la posición ys en el instante ts y el carrito parte de la posición xs con velocidad (dx/dt)s. La ecuación del movimiento del carrito es
La solución completa de esta ecuación diferencial es la suma de la homogénea y particular. La posición x y la velocidad del carrito (dx/dt) en el instante t>ts son
Dadas las condiciones iniciales, calculamos los coeficientes A y B
El bloque puede empezar a deslizar
La fuerza de rozamiento Fr entre el bloque y el plano inclinado puede alcanzar su valor máximo en el instante tk, raíz de la ecuación
Determinamos la posición xk y la velocidad (dx/dt)k, del carrito en el instante tk. La posición del bloque es ys y parte del reposo (dy/dt)k=0
La posición y velocidad del centro de masas en este instante tk es
Los dos cuerpos se mueven
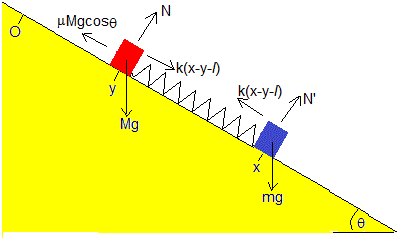
En la figura, se muestran las fuerzas sobre cada una de las partículas, las ecuaciones del movimiento son:
Movimiento del centro de masas
Movimiento relativo de las dos partículas
Se trata de la ecuación de un movimiento rectilíneo uniformemente acelerado a partir del instante tk
La solución completa es
Los coeficientes A y B se calculan a partir de la posición y velocidad de las dos partículas en el instante tk
Conocida la posición z del centro de masas y el movimiento relativo ξ, se calculan las posiciones del carrito x y del bloque y
El bloque puede detenerse
El bloque se detiene en el instante ts cuando su velocidad dy/dt=0
En el instante ts, el bloque se encuentra en la posición ys, en reposo (dy/dt)s=0, y el carrito en la posición xs con velocidad (dx/dt)s
Volvemos al apartado anterior titulado 'El bloque en reposo, el carrito se mueve'
Ejemplos
Consideremos un plano inclinado de ángulo θ=30°. El coeficiente de rozamiento (estático y cinético) entre μ=0.9 que es mayor que tanθ=0.577
- el muelle tiene una longitud l=1 m sin deformar y su constante k=10 N/m
- el bloque está situado inicialmente en la posición y=-l y su masa M=1 kg
- el carrito está situado inicialmente en el origen, y su masa m va cambiar
Con estos datos, examinaremos los distintos casos:
Si la masa m del carrito es menor que (μ/tanθ-1)/2=0.279 kg, el bloque estará en reposo. Sea m=0.2 kg
Si la masa m del carrito es mayor que (μ/tanθ-1)=0.559 kg, el bloque deslizará a lo largo del plano inclinado sin detenerse. Sea m=0.6 kg
Si la masa m del carrito está comprendida entre los dos valores límites (μ/tanθ-1)/2<m<(μ/tanθ-1), el bloque deslizará a lo largo del plano inclinado, deteniendose varias veces durante un determinado tiempo, alcanzando una posición final en reposo. Sea m=0.5 kg
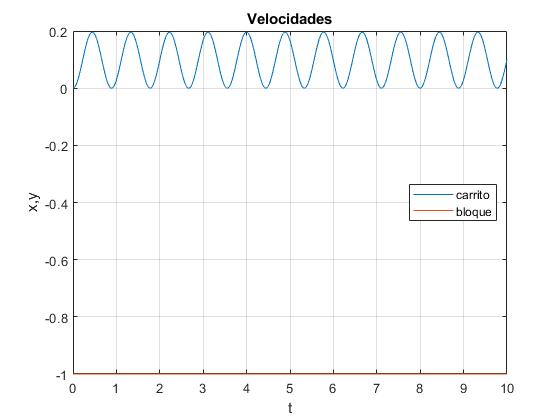
Observamos que el bloque está en reposo en la posición y=-1, y el carrito oscila con un periodo 2π/ωs=0.89 s, y un desplazamiento máximo de 0.2 m, aproximadamente
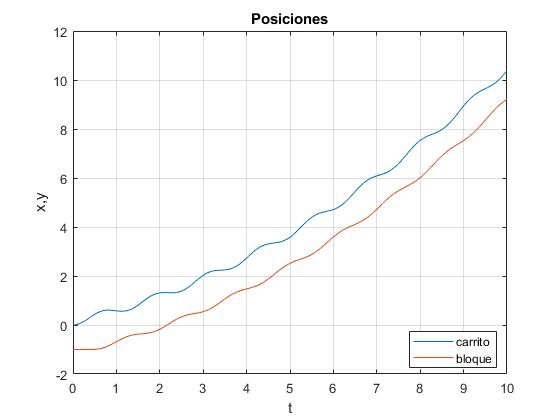
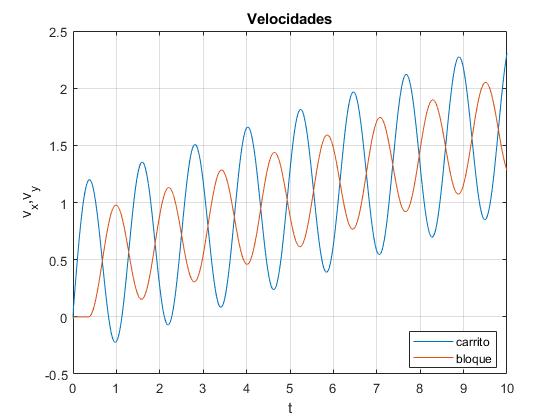
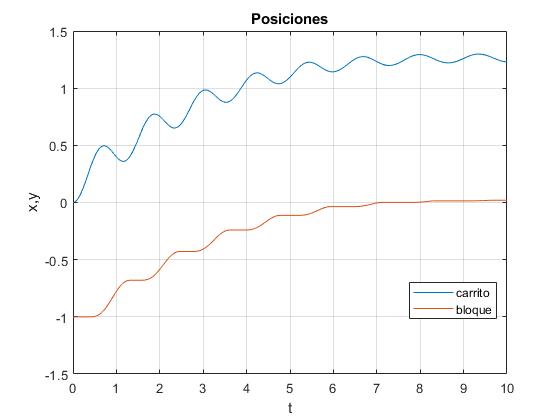
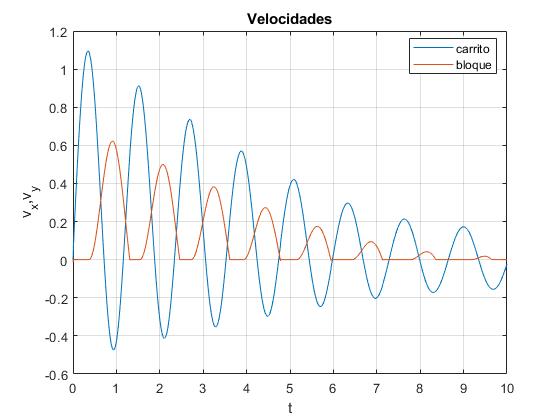
Posiciones y velocidades del bloque y el carrito
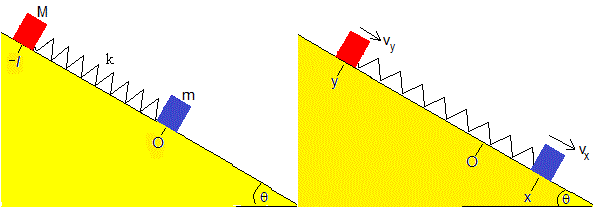
Se sitúa el carrito en el origen (x=0) y el bloque en la posición y=-l. El muelle está sin deformar, dado que μ>tanθ, el bloque se encuentra inicialmente en reposo
El script que calcula las posiciones y velociades del carrito y el bloque es el siguiente
mu=0.9; %coeficiente de rozamiento: estático y cinético
phi=pi/6; %ángulo del plano inclinado
L=1; %longitud del muelle sin deformar
m=0.5; %masa del carro
M=1; %masa del bloque
k=10; %constante del muelle
tt=0.005:0.005:10; %tiempo
xx=zeros(1,length(tt)+1); %posiciones en el instante t
yy=zeros(1,length(tt)+1);
vXX=zeros(1,length(tt)); %velocidades en el intente t
vYY=zeros(1,length(tt));
%situación inicial
y=-L; %posición inicial del bloque
x=0; %posición inicial del carro
ws=sqrt(k/m); %frecuencias angulares
wk=sqrt(k*(1/m+1/M));
ts=0; %tiempos, el bloque comienza a moverse
tk=0; %tiempos, el bloque se detiene
vY=0; %velocidad inicial del bloque
vX=0; %velocidad inicial del carro
zk=(m*x+M*y)/(m+M); %posición inicial del centro de masas
vk=0; %velocidad inicial del centro de masas
%el bloque está inicialmente en reposo mu>tan(phi)
tipo=1;
A=x-9.8*sin(phi)/ws^2-y-L;
B=vX/ws;
xx(1)=x; %posiciones iniciales
yy(1)=y;
vXX(1)=vX; %velocidades iniciales
vYY(1)=vY;
%situación en el tiempo t
i=2;
for t=tt
switch tipo
case 1 %bloque en reposo
x=A*cos(ws*(t-ts))+B*sin(ws*(t-ts))+9.8*sin(phi)/ws^2+L+y;
vX=ws*(-A*sin(ws*(t-ts))+B*cos(ws*(t-ts)));
yy(i)=y; %guarda posición y velocidad
xx(i)=x;
vXX(i)=vX;
vYY(i)=0;
if (k*(x-y-L)+M*9.8*sin(phi))>=(mu*M*9.8*cos(phi))
%empieza a deslizar
f=@(t) A*cos(ws*(t-ts))+B*sin(ws*(t-ts))-
(mu*M*cos(phi)-(m+M)*sin(phi))*9.8/k;
tk=fzero(f,t);
zk=(m*x+M*y)/(m+M); %posición inicial del centro de masas
vk=(m*vX)/(m+M); %velocidad del centro de masas
A=x-y-mu*9.8*cos(phi)/wk^2-L;
B=vX/wk;
tipo=2;
end
case 2 %bloque en movimiento
xi=A*cos(wk*(t-tk))+B*sin(wk*(t-tk))
+mu*9.8*cos(phi)/wk^2+L;
vXi=wk*(-A*sin(wk*(t-tk))+B*cos(wk*(t-tk)));
xCm=zk+vk*(t-tk)+9.8*(sin(phi)-mu*M*cos(phi)
/(m+M))*(t-tk)^2/2;
vCm=vk+9.8*(sin(phi)-mu*M*cos(phi)/(m+M))*(t-tk);
y=xCm-m*xi/(M+m);
x=xCm+M*xi/(M+m);
vY=vCm-m*vXi/(M+m);
vX=vCm+M*vXi/(M+m);
yy(i)=y; %guarda posición y velocidad
xx(i)=x;
vXX(i)=vX;
vYY(i)=vY;
%bloque se detiene
if vY<=0
vY=0;
tipo=1;
f=@(t) vk+9.8*(sin(phi)-mu*M*cos(phi)/(m+M))*(t-tk)
-wk*m*(-A*sin(wk*(t-tk))+B*cos(wk*(t-tk)))/(m+M);
ts=fzero(f,t);
A=x-9.8*sin(phi)/ws^2-L-y;
B=vX/ws;
end
end
i=i+1;
end
%plot([0,tt],vXX, [0,tt],vYY) %representa las velocidades
plot([0,tt],xx, [0,tt],yy) %representa las posiciones
legend('carrito','bloque', 'location','best')
grid on
xlabel('t')
ylabel('x,y')
%ylabel('v_x,v_y')
title('Posiciones')
%title('Velocidades')
Comprobación. Energías
Situamos el nivel cero de energía potencial en el origen
La energía inicial del sistema es Ei=Mglsinθ
La energía final Ef es la suma de
La energía cinética de las dos partículas
La energía potencial elástica del muelle deformado (x-y-l)
La energía potencial gravitatoria -(My+mx)gsinθ
La energía disipada es el trabajo de la fuerza de rozamiento cuando el bloque se desplaza (y+l), Wr=-μMgcosθ(y+l)
Comprobamos que en cada instante el trabajo de la fuerza de rozamiento Wr es igual a la diferencia entre la energía final Ef y la inicial Ei
Añadimos las siguientes líneas de código al script anterior
......
%balance energético
eMuelle=k*(xx-yy-L).^2/2;
eKin=m*vXX.^2/2+M*vYY.^2/2;
ePot=-(M*yy+m*xx)*9.8*sin(phi);
eRoza=-mu*M*9.8*cos(phi)*(yy+L);
eInicial=M*L*9.8*sin(phi);
figure
plot([0,tt],eMuelle+eKin+ePot-eInicial,[0,tt],eRoza)
grid on
legend('E_f-E_i','W_r', 'location','best')
xlabel('t')
ylabel('rozamiento')
title('Energías')
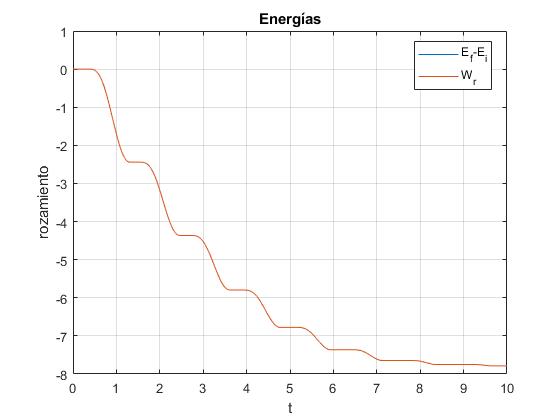
Ambas representaciones coinciden, de este modo, comprobamos que los cálculos numéricos realizados en el primer script son aproximadamente, correctos
Actividades
Se introduce
- La constante del muelle elástico k, en el control titulado k (N/m)
- El coeficiente de rozamiento μ (estático y cinético), en el control titulado μ
- la masa m del carrito, en el control titulado Masa carrito (kg)
- El ángulo del plano inclinado θ, en el control titulado Angulo
Se ha fijado
- La masa M= 1 kg del bloque
- La longitud del muelle sin deformar l= 1 m
- La posición inicial del bloque y=-l y su velocidad inicial dy/dt=0
- La posición inicial del carrito x=0 y su velocidad inicial dx/dt=0
El programa limita los valores del coeficiente de rozamiento o del ángulo del plano inclinado, de modo que se cumpla μ>tanθ, en caso contrario, un mensaje nos lo advierte
El lector puede experimentar con los tres casos descritos en esta página
- m<m1, por ejmplo, m=0.2 kg
- m>m2, por ejmplo, m=0.6 kg
- y el caso más interesante, m1<m<m2, por ejmplo, m=0.5 kg
El programa, muestra el movimiento del sistema formado por los dos cuerpos unidos por un muelle elástico a lo largo de un plano inclinado y proporciona los datos de su posición y velocidad en función del tiempo
Sobre el bloque se han dibujado dos fuerzas:
- la suma de la componente del peso a lo largo del plano inclinado y la fuerza que ejerce el muelle sobre el bloque, (en color rojo)
- El valor máximo de la fuerza de rozamiento μMgcosθ, (en color negro).
Cuando la primera se hace mayor o igual que la segunda el bloque empieza a deslizar
Referencias
I Datsenko, O Lozovenko, Yu Minaiev, M Zadoian. Paradoxes of stiff springs. Phys. Educ. 54(2019) 065003

