Una esfera situada sobre dos bloques que deslizan en un plano horizontal

Una esfera de masa m y radio R descansa sobre dos bloques de masa m cada uno y de altura R que pueden deslizar sobre un plano horizontal sin rozamiento.

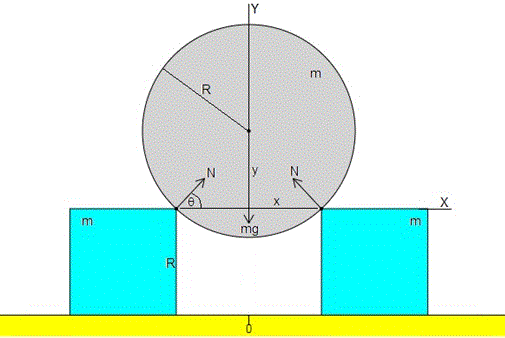
Cuando los dos bloques están juntos la esfera está en equilibrio inestable, se separan un poco y la esfera se mueve hacia abajo empujando a los bloques a uno y otro lado, tal como se muestra en la figura.

En la figura, se muestran las fuerzas sobre la esfera

• El peso mg
• La fuerza que ejercen los bloques sobre la esfera, N

La ecuación del movimiento de la esfera a lo largo del eje Y es

ma_y=2Nsinθ-mg

Como los bloques se mueven a lo largo del plano horizontal sin rozamiento, la esfera ejerce una fuerza horizontal Ncosθ sobre cada uno de los bloques. La ecuación del movimiento de cada bloque es

ma_x=Ncosθ

a_x es la aceleración de los bloques y a_y es la aceleración del centro de la esfera

Conservación de la energía

Por otra parte, el sistema es conservativo y la energía permanece constante

${\displaystyle mgR=mgy+\frac{1}{2}m{v}_y^2+2\frac{1}{2}m{v}_x^2}$

y=R es la altura inicial del centro de la esfera

Posiciones

• La posición de un bloque es x
• La posición del centro de la esfera es y

Ambas posiciones están relacionadas, x²+y²=R²

Velocidades

Las velocidades también están relacionadas

${\displaystyle \begin{array}{l}2x\frac{dx}{dt}+2y\frac{dy}{dt}=0\\ v_x=-\frac{y}{x}{v}_y\end{array}}$

En la ecuación de la conservación de la energía despejamos la velocidad v_y

${\displaystyle \begin{array}{l}gR=gy+\left(\frac{1}{2}+\frac{y^2}{x^2}\right)v_y^2\\ v_y^2=2g\frac{\left(R^2-y^2\right)\left(R-y\right)}{R^2+y^2}\end{array}}$

Utilizando la relación entre v_x y v_y, despejamos v_x

${\displaystyle v_x^2=2g{y}^2\frac{R-y}{R^2+y^2}}$

Aceleraciones

• Conocida la velocidad v_y, calculamos la aceleración a_y del centro de la esfera

${\displaystyle \begin{array}{l}2v_y\frac{d{v}_y}{dt}=2g\frac{\left(-R^2-2Ry+3y^2\right)\left(R^2+y^2\right)-2y\left(R^3-R^{2}y-R{y}^2+y^3\right)}{{\left(R^2+y^2\right)}^2}\frac{dy}{dt}\\ \frac{d{v}_y}{dt}=g\frac{-R^4-4R^{3}y+4R^2{y}^2+y^4}{{\left(R^2+y^2\right)}^2}\end{array}}$

• Conocida la velocidad v_x, calculamos la aceleración a_x de cada uno de los bloques

${\displaystyle \begin{array}{l}2v_x\frac{d{v}_x}{dt}=2g\frac{2R^{3}y-3R^2{y}^2-y^4}{{\left(R^2+y^2\right)}^2}\frac{dy}{dt}\\ \frac{d{v}_x}{dt}=g\frac{2R^{3}y-3R^2{y}^2-y^4}{{\left(R^2+y^2\right)}^2}\frac{v_y}{v_x}\\ \frac{d{v}_x}{dt}=-g\frac{2R^3-3R^{2}y-y^3}{{\left(R^2+y^2\right)}^{3/2}}\end{array}}$

La aceleración a_x se anula y por tanto, la reacción N a la altura y₀, raíz de la ecuación cúbica

${\displaystyle y^3+3R^{2}y-2R^3=0}$

Esta ecuación es de la forma x³+ax²+bx+c=0, a=0, b=3, c=-2, con x=y/R

Utilizamos la función raices_3 para calcular las raíces de la ecuación cúbica. Alternativamente, se puede utilizar la función roots de MATLAB

function esfera
    raiz=raices_3([1,0,3,-2]);
    disp(raiz)

    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

   0.5961 + 0.0000i
  -0.2980 + 1.8073i
  -0.2980 - 1.8073i

La raíz real es y₀/R=0.5961

Obtenemos la raíz real utilizando Math Symbolic de MATLAB

a=sym(0);
b=sym(3);
c=sym(-2);
P=b-a^2/3;
Q=a*b/3-c-2*a^3/27;
v3=-Q/2+sqrt((Q/2)^2+(P/3)^3); %una de las raíces, la otra con (-)
v=zeros(0,3);
k=sym(0:2);
v=abs(v3)^(1/3)*exp(1i*(angle(v3)+k*2*pi)/3);
u=P./(3*v);
x=u-v; %raíces de la ecuación reducida
z=x-a/3 %raíces de la ecuación de tercer grado

z =[1/(2^(1/2) - 1)^(1/3) - (2^(1/2) - 1)^(1/3), 
- ((3^(1/2)*1i)/2 - 1/2)*(2^(1/2) - 1)^(1/3) + 1/(((3^(1/2)*1i)/2 - 1/2)
*(2^(1/2) - 1)^(1/3)), ((3^(1/2)*1i)/2 + 1/2)*(2^(1/2) - 1)^(1/3) - 1/
(((3^(1/2)*1i)/2 + 1/2)*(2^(1/2) - 1)^(1/3))]

La raíz real está en la primera fila

${\displaystyle \frac{y_0}{R}=\frac{1}{\sqrt[3]{\sqrt{2}-1}}-\sqrt[3]{\sqrt{2}-1}}$

Para y≤y₀, la reacción N es cero y la esfera cae libremente, bajo la acción únicamente de su propio peso

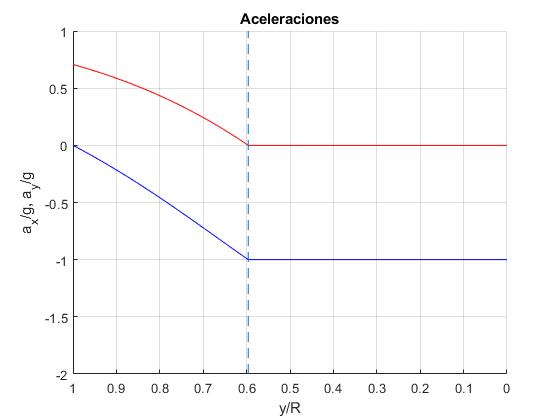
Representamos a_x/g (color rojo) y a_y/g (color azul) en función de y/R en el intervalo [1,0]. La línea vertical corresponde a y₀/R, posición en la que a_x=0, N=0, a partir de esta posición y≤y₀, las aceleraciones a_x=0 y a_y=-g

R=1;
hold on
y0=((1+sqrt(2))^(1/3)-1/(1+sqrt(2))^(1/3))*R;
ax=@(y) -(2-3*y-y.^3)./(1+y.^2).^(3/2);
fplot(ax,[y0,1], 'color','r');
line([0,y0],[0,0],'color','r')
ay=@(y) (-1-4*y+4*y.^2+y.^4)./(1+y.^2).^2;
fplot(ay,[y0,1], 'color','b');
line([0,y0],[-1,-1],'color','b')
line([y0,y0],[-2,1],'LineStyle','--')
hold off
set(gca, 'XDir','reverse')
xlabel('y/R')
ylabel('a_x/g, a_y/g')
grid on
title('Aceleraciones')

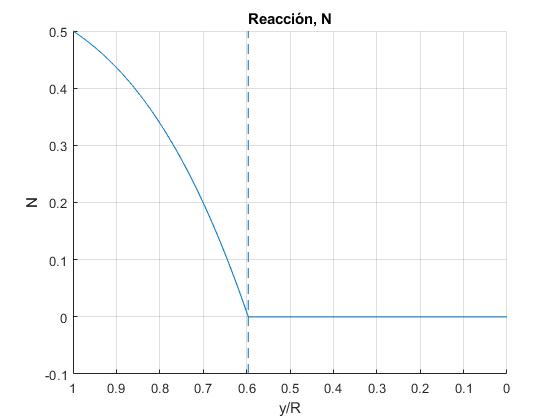
Representamos la reacción N en función de y/R

y0=((1+sqrt(2))^(1/3)-1/(1+sqrt(2))^(1/3))*R;
ay=@(y) (-1-4*y+4*y.^2+y.^4)./(1+y.^2).^2;
N=@(y) (ay(y)+1)*R./(2*y);
fplot(N,[y0,1]);
line([0,y0],[0,0])
line([y0,y0],[-0.1,0.5], 'lineStyle','--')
set(gca, 'XDir','reverse')
xlabel('y/R')
ylabel('N')
grid on
title('Reacción, N')

Comprobación, cuando a_x=0, es decir, y³+3R²y-2R³=0, entonces a_y=-g

${\displaystyle \frac{d{v}_y}{dt}=g\frac{-R^4-4R^{3}y+4R^2{y}^2+y^4}{{\left(R^2+y^2\right)}^2}=g\frac{-R^4-2\left(y^3+3R^{2}y\right)y+4R^2{y}^2+y^4}{{\left(R^2+y^2\right)}^2}=-g\frac{R^4+2R^2{y}^2+y^4}{{\left(R^2+y^2\right)}^2}=-g}$

Etapas del movimiento

• En el intervalo y₀<y<R la aceleración del centro de la esfera es a_y y la del bloque a_x

Integramos la ecuación diferencial por procedimientos numéricos

${\displaystyle \frac{dy}{dt}=\sqrt{2g\frac{\left(R^2-y^2\right)\left(R-y\right)}{R^2+y^2}}}$

Con la siguiente condición inicial, en el instante t=0, el centro de la esfera parte de la posición y=0.999R, desplazado de la posición de equilibrio inestable.

y es la posición del centro de la esfera, y $x=\sqrt{R^2-y^2}$, es la posición de cada bloque

• En el intervalo, 0<y<y₀, la aceleración del centro de la esfera es -g y el bloque se mueve con velocidad constante

En y₀, la velocidad de la esfera es v_0y y la del bloque v_0x

${\displaystyle v_{0x}=y_0\sqrt{2g\frac{R-y_0}{R^2+y_0^2}},v_{0y}=\sqrt{2g\frac{\left(R^2-y_0^2\right)\left(R-y_0\right)}{R^2+y_0^2}}}$

sus valores son, v_0x=1.4407 m/s y v_0y=1.9406 m/s, para R=1 m

Las ecuaciones del movimiento del centro de la esfera y de los bloques son

${\displaystyle \begin{array}{l}\{\begin{array}{l}y=y_0-v_{0y}\left(t-t_0\right)-\frac{1}{2}g{\left(t-t_0\right)}^2\\ v_y=v_{0y}-g\left(t-t_0\right)\end{array}\\ \{\begin{array}{l}x=x_0+v_{0x}\left(t-t_0\right)\\ v_{0x}=\text{cte}\end{array}\end{array}}$

t₀ es el instante en el que el centro de la esfera alcanza la posición y₀ y $x_0=\sqrt{R^2-y_0^2}$

La velocidad de la esfera cuando impacta en el plano horizontal es

${\displaystyle \begin{array}{l}t=t_0+\frac{-v_{0y}+\sqrt{v_{0y}^2+2g{y}_0}}{g}\\ v_y=v_{0y}+g\left(t-t_0\right)=\sqrt{v_{0y}^2+2g{y}_0}\end{array}}$

Su valor es v_y=3.9305 m/s

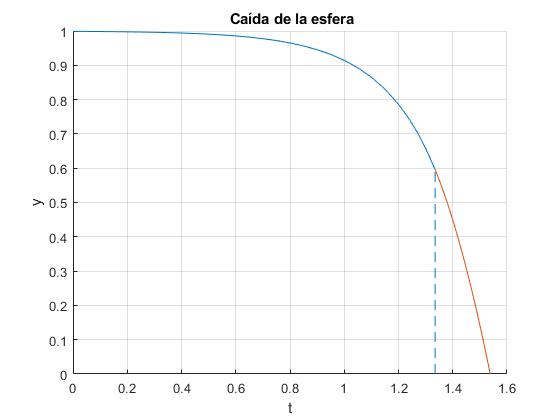
Representamos la posición y del centro de la esfera en función del tiempo t

function esfera_1
    R=1;
    y0=((1+sqrt(2))^(1/3)-1/(1+sqrt(2))^(1/3))*R;
    f=@(t,y) -(R-y)*sqrt(2*9.8*(R+y)/(R^2+y^2)); 
    opts=odeset('events',@stop_esfera);
    [t,y]=ode45(f,[0,2],0.999*R, opts); 
    hold on
    plot(t,y)
    v0y=sqrt(2*9.8*(R^2-y0^2)*(R-y0)/(R^2+y0^2));
    t0=t(end); %tiempo final 
    yy=@(t) y0-v0y*(t-t0)-4.9*(t-t0).^2;
    tFin=(-v0y+sqrt(v0y^2+2*9.8*y0))/9.8;
    fplot(yy, [t0, t0+tFin])
    line([t0,t0],[0,y0], 'lineStyle','--')
    hold off
    xlabel('t')
    ylabel('y')
    grid on
    title(' Caída de la esfera')
    
    function [value,isterminal,direction]=stop_esfera(~,x)
        value=x-y0;
        isterminal=1;  
        direction=-1; 
    end
end

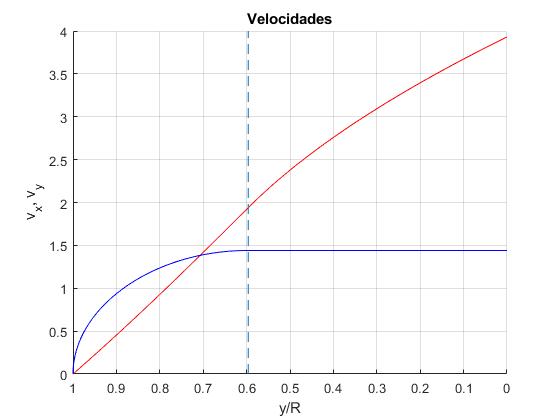
Representamos las velocidades v_x (color azul) del bloque y v_y (color rojo) del centro de la esfera en función de y

hold on
y0=((1+sqrt(2))^(1/3)-1/(1+sqrt(2))^(1/3))*R;
vy=@(y) sqrt(2*9.8*R*(1-y.^2).*(1-y)./(1+y.^2));
fplot(vy,[y0,1], 'color','r');
vyy=@(y) sqrt(vy(y0)^2+2*9.8*(y0-y));
fplot(vyy, [0,y0],'color','r')
vx=@(y) (y/sqrt(R)).*sqrt(2*9.8*(1-y)./(1+y.^2));
fplot(vx,[y0,1], 'color','b');
line([0,y0],[vx(y0),vx(y0)],'color','b')
line([y0,y0],[0,4], 'lineStyle','--')
hold off
set(gca, 'XDir','reverse')
xlabel('y')
ylabel('v_x, v_y')
grid on
title('Velocidades')

Actividades

Mostramos el movimiento de la esfera y de los dos bloques

Se pulsa el botón titulado Nuevo

Una cúpula semiesférica móvil

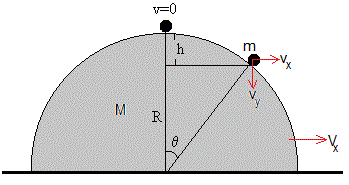
Una partícula de masa m desliza sin rozamiento sobre una cúpula semiesférica de masa M y radio R. La cúpula puede deslizar sin rozamiento sobre el plano horizontal. Vamos a calcular el ángulo θ_c para el cual la partícula deja de estar en contacto con la cúpula.

El problema para una cúpula semiesférica fija ha sido estudiado en la página titulada Movimiento sobre una cúpula semiesférica (sin rozamiento)

Las fuerzas externas e internas que actúan en el sistema formado por la partícula y la cúpula semiesférica son:

• El peso de la partícula, mg y de la cúpula, Mg
• La reacción del plano horizontal sobre la cúpula. Todas ellas verticales
• Una fuerza interna, la reacción N, que es la fuerza que ejerce la cúpula sobre la partícula, igual y de sentido contrario a la que ejerce la partícula sobre la cúpula

Conservación del momento lineal

No hay fuerzas externas en la dirección horizontal, se conserva el momento lineal.

${\displaystyle m{v}_x+M{V}_x=0}$

Supondremos que la partícula parte del vértice de la cúpula en reposo y la cúpula está inicialmente en reposo. v_x es la componente horizontal de la velocidad de la partícula y v_y es la componente vertical. V_x es la velocidad de la cúpula cuando la posición de la partícula es θ

Conservación de la energía

Aplicamos el principio de conservación de la energía. La energía potencial de la partícula correspondiente a la altura h se transforma en energía cinética de la partícula y de la cúpula

${\displaystyle \begin{array}{l}mg\left(R-R\cos \theta \right)=\frac{1}{2}M{V}_x^2+\frac{1}{2}m\left(v_x^2+v_y^2\right)\\ mgR\left(1-\cos \theta \right)=\frac{1}{2}M{\left(-\frac{m}{M}{v}_x\right)}^2+\frac{1}{2}m\left(v_x^2+v_y^2\right)\\ 2gR\left(1-\cos \theta \right)=\left(1+\frac{m}{M}\right)v_x^2+v_y^2\end{array}}$

Dinámica del movimiento circular

En el Sistema de Referencia ligado a la cúpula la componente horizontal u_x de la velocidad de la partícula es

${\displaystyle \begin{array}{l}{u}_x=v_x-V_x=\left(1+\frac{m}{M}\right)v_x\\ u_y=v_y\end{array}}$

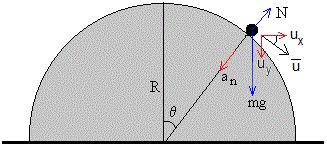
La velocidad relativa $\overrightarrow{u}$, es tangente a la trayectoria circular, su módulo es

${\displaystyle \begin{array}{l}{u}^2={\left(1+\frac{m}{M}\right)}^2{v}_x^2+v_y^2\\ \cos \theta =\frac{\left(1+\frac{m}{M}\right)v_x}{u}\\ v_y^2={\left(1+\frac{m}{M}\right)}^2\left(\frac{1}{{\cos }^2\theta }-1\right)v_x^2\end{array}}$

La partícula deja de estar en contacto con la cúpula en la posición θ_c cuando la reacción N=0, las velocidades V_x y v_x son constantes y la única fuerza que actúa sobre la partícula es el peso mg. De la dinámica del movimiento circular

${\displaystyle \begin{array}{l}mg\cos \theta =m\frac{u^2}{R}\\ gR\cos \theta =\frac{{\left(1+\frac{m}{M}\right)}^2{v}_x^2}{{\cos }^2\theta }\\ {\left(1+\frac{m}{M}\right)}^2{v}_x^2=gR{\cos }^3\theta \end{array}}$

Angulo crítico

Sustituimos en la ecuación de la conservación de la energía v_x y v_y y llamamos r=m/M

${\displaystyle \begin{array}{l}2gR\left(1-\cos \theta \right)=\left(1+r\right)v_x^2+\left\{{\left(1+r\right)}^2\left(\frac{1}{{\cos }^2\theta }-1\right)\right\}{v}_x^2\\ 2gR\left(1-\cos \theta \right)=\left(1+r\right)\left\{1+\left(1+r\right)\left(\frac{1}{{\cos }^2\theta }-1\right)\right\}\frac{gR{\cos }^3\theta }{{\left(1+r\right)}^2}\\ r{\cos }^3{\theta }_c-3(1+r)\cos {\theta }_c+2(1+r)=0\\ {\cos }^3{\theta }_c-3\left(\frac{1}{r}+1\right)\cos {\theta }_c+2\left(\frac{1}{r}+1\right)=0\end{array}}$

El coseno del ángulo crítico θ_c es la raíz positiva menor o igual que la unidad de la ecuación de tercer grado

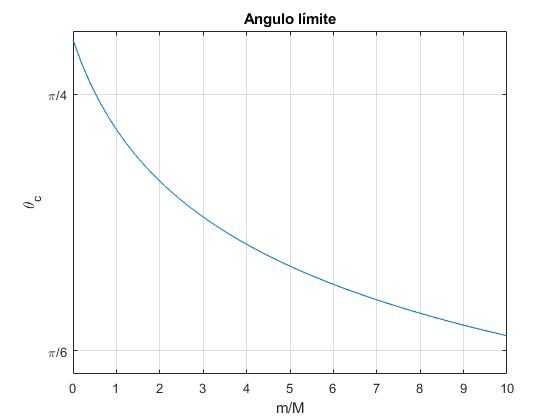
Casos particulares:

• Cuando r=0, (una cúpula de masa infinita), cosθ_c=2/3. Resultado ya obtenido

• Para r=1

${\displaystyle \begin{array}{l}{\cos }^3{\theta }_c-6\cos {\theta }_c+4=0\\ (\cos {\theta }_c-2)({\cos }^2{\theta }_c+2\cos {\theta }_c-2)=0\\ \cos {\theta }_c=\frac{-2+\sqrt{12}}{2}=-1+\sqrt{3},{\theta }_c=42.9º\end{array}}$

• Cuando r→∞

${\displaystyle \begin{array}{l}{\cos }^3{\theta }_c-3\cos {\theta }_c+2=0\\ {\left(\cos {\theta }_c-1\right)}^2(\cos {\theta }_c+2)=\mathrm{0,}{\theta }_c=0\end{array}}$

Representamos el ángulo θ_c en función de r=m/M. Para obtener las raíces de la ecuación cúbica, utilizamos la función raices_3. Alternativamente, podríamos utilizar la función roots de MATLAB

function cupula
    rr=linspace(0,10,50);
    th=zeros(1,length(rr));
    th(1)=acos(2/3);
    i=2;
    for r=rr(2:end)
        raiz=raices_3([1,0,-3*(1/r+1),2*(1/r+1)]);
        for k=1:3
            if abs(raiz(k))<=1
                th(i)=acos(raiz(k));
                i=i+1;
                break;
            end
        end
    end
    plot(rr,th)
    set(gca,'YTick',0:pi/12:pi/3)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3'})
    xlabel('m/M')
    ylabel('\theta_c')
    grid on
    title('Angulo límite')

    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

Referencias

En la página siguiente