Fuegos artificiales

Sea un proyectil de masa m₁+m₂ que se dispara con velocidad inicial v₀, haciendo un ángulo θ con la horizontal. Cuando llega al punto más alto de su trayectoria hace explosión y se divide en dos fragmentos, separándose en dirección horizontal y en el plano de la trayectoria parabólica. Vamos a determinar la trayectoria de cada uno de los dos fragmentos y a calcular su alcance o la distancia de sus puntos de impacto en el suelo al origen.

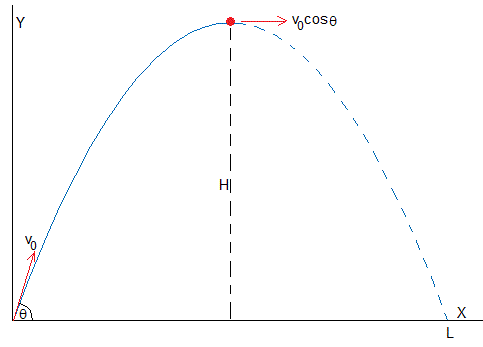
Trayectoria del centro de masas

${\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = v_{0} \cdot \cos θ \\ v_{y} = v_{0} \cdot sin θ - g \cdot t \end{cases} {\begin{cases} x = v_{0} \cdot \cos θ \cdot t \\ y = v_{0} \cdot sin θ \cdot t - \frac{1}{2} g \cdot t^{2} \end{cases}$

El punto más alto de la trayectoria se calcula poniendo v_y=0, t=v₀sinθ/g

$H = v_{0} \sin θ \frac{v_{0} \sin θ}{g} - \frac{1}{2} g {(\frac{v_{0} \sin θ}{g})}^{2} = \frac{v_{0}^{2} \sin^{2} θ}{2 g}$

El centro de masas impacta en el suelo y=0, en el instante

$T = \frac{2 v_{0} \sin θ}{g}$

que se denomina tiempo de vuelo. El c.m. impacta a una distancia L del origen, denominado alcance

$L = v_{0} \cos θ (\frac{2 v_{0} \sin θ}{g}) = \frac{v_{0}^{2}}{g} \sin (2 θ)$

Explosión en dos fragmentos

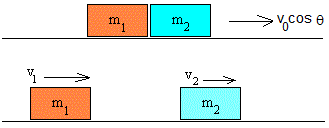
En el punto más alto de la trayectoria, el proyectil que lleva una velocidad horizontal v₀cosθ hace explosión dividiéndose en dos fragmentos. Supondremos que los dos fragmentos se mueven inicialmente en la misma dirección (eje X) y en el plano de la trayectoria (X, Y).

Aplicamos el principio de conservación del momento lineal y el balance energético a la colisión

$\begin{array}{l} (m_{1} + m_{2}) v_{0} \cos θ = m_{1} v_{1} + m_{2} v_{2} \\ \frac{1}{2} (m_{1} + m_{2}) {(v_{0} \cos θ)}^{2} + Q = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} \end{array}$

Despejamos v₁ y v₂ de este sistema de ecuaciones

$\begin{array}{l} v_{2}^{2} - 2 v_{0} \cos θ \cdot v_{2} + v_{0}^{2} \cos^{2} θ - 2 Q \frac{m_{1}}{(m_{1} + m_{2}) m_{2}} = 0 \\ v_{2} = v_{0} \cos θ + \sqrt{2 Q \frac{m_{1}}{(m_{1} + m_{2}) m_{2}}} \\ v_{1}^{2} - 2 v_{0} \cos θ \cdot v_{1} + v_{0}^{2} \cos^{2} θ - 2 Q \frac{m_{2}}{(m_{1} + m_{2}) m_{1}} = 0 \\ v_{1} = v_{0} \cos θ - \sqrt{2 Q \frac{m_{2}}{(m_{1} + m_{2}) m_{1}}} \end{array}$

Supondremos que la energía de la explosión Q es una fracción f de la energía cinética de la partícula en el punto más alto de la trayectoria.

$\begin{array}{l} Q = f \frac{1}{2} (m_{1} + m_{2}) {(v_{0} \cos θ)}^{2} \\ v_{1} = v_{0} \cos θ (1 - \sqrt{f \frac{m_{2}}{m_{1}}}) \\ v_{2} = v_{0} \cos θ (1 + \sqrt{f \frac{m_{1}}{m_{2}}}) \end{array}$

Movimiento de los fragmentos después de la explosión

Las ecuaciones del movimiento de los dos fragmentos son similares. La ecuación del movimiento del primer fragmento es

${\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = v_{1} \\ v_{y} = 0 \end{cases} {\begin{cases} x = \frac{L}{2} + v_{1} \cdot t \\ y = H - \frac{1}{2} g \cdot t^{2} \end{cases}$

El punto de impacto en el suelo y=0, se produce en el instante

$t = \sqrt{\frac{2 H}{g}} = \frac{T}{2}$

El alcance del primer fragmento o distancia del punto de impacto en el suelo al origen es

$x_{1} = \frac{L}{2} + v_{1} \frac{T}{2}$

De modo similar, El alcance del segundo fragmento es

$x_{2} = \frac{L}{2} + v_{2} \frac{T}{2}$

Comprobamos que la posición del centro de masa es x_cm=L

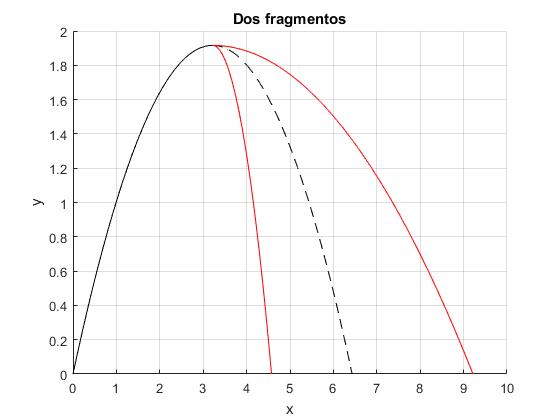
$x_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}} = (\frac{L}{2} + v_{0} \cos θ \frac{T}{2}) + \frac{m_{2} \sqrt{f \frac{m_{1}}{m_{2}}} - m_{1} \sqrt{f \frac{m_{2}}{m_{1}}}}{m_{1} + m_{2}} = L$

Representamos la trayectoria del proyectil y la de los dos fragmentos. La línea a trazos representa la trayectoria del centro de masa de los dos fragmentos. La energía Q de la explosión es una fracción f de la energía cinética del proyectil en el punto más alto. Se sugiere modificar la velocidad inicial v₀, el ángulo de tiro θ el cociente m=m₁/m₂ de las masas de los fragmentos y el valor de la fracción f

v0=8; %velocidad inicial
th=50*pi/180; %ángulo
m=1.5; %cociente m2/m1
 
H=(v0*sin(th))^2/(2*9.8); %altura máxima
L=v0^2*sin(2*th)/9.8; %alcance
T=2*v0*sin(th)/9.8; %tiempo de vuelo
f=0.5; %fracción
 
%después de la explosión
v1=v0*cos(th)*(1+sqrt(f*m));
v2=v0*cos(th)*(1-sqrt(f/m));
hold on
fplot(@(t) v0*cos(th)*t, @(t) v0*sin(th)*t-4.9*t.^2, [0,T/2], 'color','k')
fplot(@(t) v0*cos(th)*t, @(t) v0*sin(th)*t-4.9*t.^2, [T/2,T], 
'lineStyle','--','color','k')
fplot(@(t) L/2+v1*t, @(t) H-4.9*t.^2, [0,T/2], 'color','r')
fplot(@(t) L/2+v2*t, @(t) H-4.9*t.^2, [0,T/2], 'color','r')
hold off
grid on
xlabel('x')
ylabel('y')
title('Dos fragmentos')

Actividades

Se introduce

La velocidad v₀ de disparo en el contro titulado V. disparo
El ángulo θ, de tiro, en el control titulado Angulo
El cociente m₂/m₁ de las masas en el control titulado Cociente m2/m1
La fracción f de la energía cinética de la partícula en el punto más alto de su trayectoria, en el control titulado Fracción

Se pulsa el botón titulado Nuevo.

V.disparo, v₀ Angulo, θ
Cociente, m₂/m₁ Fracción, f

Fuegos artificiales

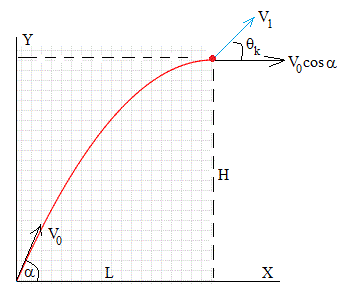
Se dispara un explosivo de masa M con velocidad V₀ haciendo un ángulo α con la horizontal. Las ecuaciones del movimiento son

$\vec{a} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} \vec{v} {\begin{cases} v_{x} = V_{0} \cos α \\ v_{y} = V_{0} \sin α - g t \end{cases} \vec{r} {\begin{cases} x = V_{0} \cos α \cdot t \\ y = V_{0} \sin α \cdot t - \frac{1}{2} g t^{2} \end{cases}$

Alcanza la altura máxima v_y=0, en el instante t=V₀sinα/g, su posición es

$L = \frac{V_{0}^{2} \sin (2 α)}{2 g} H = \frac{V_{0}^{2} \sin^{2} α}{2 g}$

En este instante, explota en N trozos iguales que salen disparados con la misma velocidad V₁ en N direcciones que forman ángulos iguales entre sí.

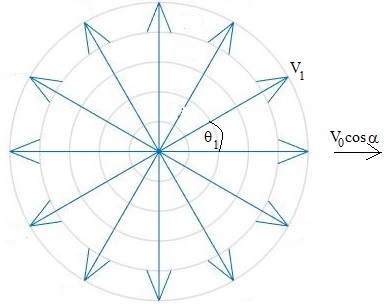
Las ecuaciones del movimiento de un trozo que forma un ángulo θ_k con la horizontal son

$\vec{a} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} \vec{v} {\begin{cases} v_{x} = V_{0} \cos α + V_{1} \cos θ_{k} \\ v_{y} = V_{1} \sin θ_{k} - g t \end{cases} \vec{r} {\begin{cases} x = L + (V_{0} \cos α + V_{1} \cos θ_{k}) t \\ y = H + V_{1} \sin θ_{k} \cdot t - \frac{1}{2} g t^{2} \end{cases}$

El momento lineal justamente antes de la explosión es igual al momento lineal después de la explosión. El centro de masas del sistema de partículas después de la explosión sigue la trayectoria parabólica original bajo la acción de la única fuerza externa peso.

$\begin{array}{l} \vec{P_{f}} = \frac{M}{N} {\sum^{}}_{N}^{k = 1} \vec{V_{k}} = \frac{M}{N} {\sum^{}}_{N}^{k = 1} (V_{0} \cos α + V_{1} \cos θ_{k}) \hat{i} + \frac{M}{N} {\sum^{}}_{N}^{k = 1} (V_{1} \sin θ_{k}) \hat{j} = \\ M V_{0} \cos α \hat{i} + \frac{M}{N} V_{1} {\sum^{}}_{N}^{k = 1} (\cos θ_{k} \hat{i} + \sin θ_{k} \hat{j}) = M V_{0} \cos α \hat{i} \end{array}$

Por simetría (véase la figura anterior) el sumatorio se hace cero, quedando el momento lineal final, igual al inicial en el momento de la explosión

Actividades

Se introduce

El ángulo α, en el control titulado Angulo
La velocidad V₁ de cada uno de las partículas en el control titulado Velocidad.
La velocidad V₀ de disparo del explosivo se ha fijado en 10 m/s

Se pulsa el botón titulado Nuevo.

Velocidad (m/s)
Angulo

Referencias

R De Luca, O Faella. Simple mathematical fireworks. Eur. J. Phys. 35 (2014) pp. 1, 8