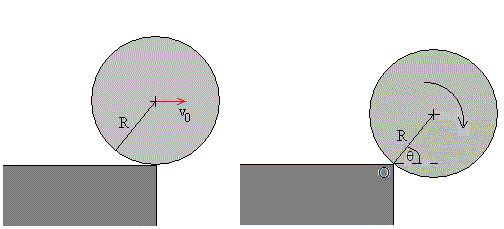
El peso actuando en el centro de masas proporciona el momento que provoca el movimiento de rotación del c.m. de la bola alrededor de un eje que pasa por el borde O de la mesa, mientras que la fuerza de rozamiento evita el deslizamiento de la bola hasta el momento que alcanza un ángulo crítico. A partir de ese momento, la bola desliza sobre el borde, hasta que la reacción N se hace cero. Finalmente, la bola cae bajo la acción de su peso. Calcularemos para esta etapa del movimiento la velocidad inicial del centro de masas y la velocidad angular inicial de rotación alrededor de un eje que pasa por el c.m..

Coordendas polares

Para estudiar el movimiento de la bola utilizaremos las coordenadas polares. En una página previa hemos deducido la expresión del vector velocidad y el vector aceleración en coordenadas polares.

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\hfill \\ \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Para describir el movimiento de la bola adoptamos el sistema de referencia mostrado en la segunda figura, más arriba.

Primera etapa del movimiento

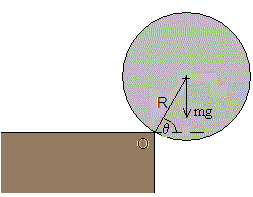
Aplicando Steiner, el momento de inercia de la esfera respecto de un eje perpendicular al plano de la figura que para por O es

${\displaystyle I_O=\frac{2}{5}m{R}^2+m{R}^2=\frac{7}{5}m{R}^2}$

La ecuación de la dinámica de rotación de la esfera alrededor de un eje perpendicular al plano de la figura y que pasa por O

${\displaystyle \begin{array}{l}\left(\frac{7}{5}m{R}^2\right)\frac{d^2\theta }{d{t}^2}=-mgR\cos \theta \\ \frac{d^2\theta }{d{t}^2}=-\frac{5}{7}\frac{g}{R}\cos \theta \end{array}}$

Integramos esta ecuación, con las condiciones iniciales siguientes: θ=π/2, ω₀ =v₀/R.

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=-\frac{5}{7}\frac{g}{R}\cos \theta \\ \frac{d\omega }{d\theta }\frac{d\theta }{dt}=-\frac{5}{7}\frac{g}{R}\cos \theta \omega \frac{d\omega }{d\theta }=-\frac{5}{7}\frac{g}{R}\cos \theta \\ {\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\omega ·d\omega =}-\frac{5}{7}\frac{g}{R}{\displaystyle \underset{\pi /2}{\overset{\theta }{\int }}\cos \theta ·d\theta }\\ \frac{1}{2}{\omega }^2-\frac{1}{2}{\omega }_0^2=\frac{5}{7}\frac{g}{R}(1-\sin \theta )\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{10}{7}\frac{g}{R}(1-\sin \theta )+{\omega }_0^2\end{array}}$

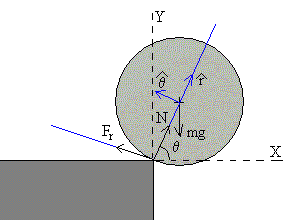
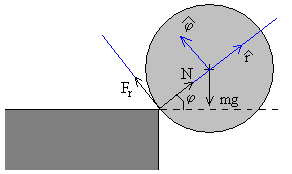
Las fuerzas que actúan sobre la bola son:

• El peso, mg
• La fuerza que ejerce la mesa sobre la bola, la fuerza normal N
• La fuerza de rozamiento entre el borde de la mesa y la bola, F_r

Teniendo en cuenta que r=R es constante, las ecuaciones del movimiento del c.m. en la dirección radial $\widehat{r}$ y en la dirección $\widehat{\theta }$ son, respectivamente,

${\displaystyle \begin{array}{l}-mR{\left(\frac{d\theta }{dt}\right)}^2=N-mg\sin \theta \\ mR\frac{d^2\theta }{d{t}^2}=F_r-mg\cos \theta \end{array}}$

La ecuación de la dinámica de rotación alrededor de un eje que pasa por el c.m. es

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=-F_{r}R{I}_c=\frac{2}{5}m{R}^2}$

Combinado estas dos últimas ecuaciones obtenemos,

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{5}{7}\frac{g}{R}\cos \theta }$

Conocida la aceleración angular, calculamos la fuerza de rozamiento F_r. Conocida la velocidad angular calculamos la reacción del borde N

${\displaystyle \begin{array}{l}N=\frac{17}{7}mg\sin \theta -mR{\omega }_0^2-\frac{10}{7}mg\\ F_r=\frac{2}{7}mg\cos \theta \end{array}}$

La fuerza de rozamiento F_r va creciendo a medida que disminuye el ángulo θ, hasta que alcanza el valor máximo μ_sN momento en el que la bola empieza a deslizar sobre el borde. μ_s es el coeficiente estático de rozamiento. El ángulo crítico θ₁ para el cual F_r= μ_sN es

${\displaystyle {\mu }_s\left(17g\sin {\theta }_1-7R{\omega }_0^2-10g\right)=2g\cos {\theta }_1}$

Para calcular θ₁, se resuelve esta ecuación trascendente por procedimientos numéricos

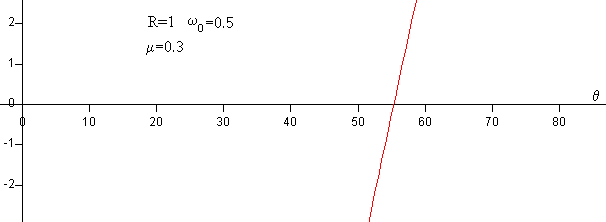
En la figura se representa la función

${\displaystyle {\mu }_s\left(17g\sin \theta -7R{\omega }_0^2-10g\right)-2g\cos \theta }$

Para μ_s=0.3 y ω₀ =0.5 rad/s. El ángulo para el cual la función se hace cero es aproximadamente, 55º

Para calcular el ángulo que gira el c.m. de la bola en función del tiempo hay que resolver por procedimientos numéricos la ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{5}{7}\frac{g}{R}\cos \theta }$

con las siguientes condiciones iniciales: en el instante t=0, θ=π/2, dθ/dt=ω₀.

Se termina la primera etapa del movimiento en el instante t₁ cuando la posición del c.m. de la bola es θ₁ y lleva una velocidad angular.

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_1=\sqrt{\frac{10}{7}\frac{g}{R}(1-\sin {\theta }_1)+{\omega }_0^2}}$

Ejemplo.

• Sea una bola de R=1.0 m de radio
• El coeficiente estático de rozamiento es μ_s=0.3
• La velocidad inicial del c.m. des v₀=0.5 m/s, la velocidad angular inicial de rotación es ω₀=v₀/R=0.5 rad/s.

Resolvemos la ecuación trascendente y obtenemos θ₁=55.3º que es el ángulo girado por el c.m. al concluir la primera etapa del movimiento.

La posición del c.m. es

x_c=R ·cos θ₁=0.57 m
y_c=R ·sin θ₁=0.82 m

La velocidad angular de rotación vale,

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_1=\sqrt{\frac{10}{7}\frac{9.8}{1.0}(1-\sin 55.3)+{0.5}^2}=1.65\text{rad/s}}$

Segunda etapa del movimiento.

El punto de contacto de la bola desliza sobre el borde de la mesa.

Las ecuaciones del movimiento del c.m. en la dirección radial $\widehat{r}$ y en la dirección $\widehat{\theta }$ son, respectivamente,

${\displaystyle \begin{array}{l}-mR{\left(\frac{d\phi }{dt}\right)}^2=N-mg\sin \phi \\ mR\frac{d^2\phi }{d{t}^2}=F_r-mg\cos \phi \end{array}}$

Como la bola está deslizando, la relación entre la fuerza de rozamiento y la fuerza normal es

F_r=μ_k·N

Donde μ_k es el coeficiente cinético

Combinando las tres primeras ecuaciones, el movimiento del c.m. está descrito por la ecuación diferencial

${\displaystyle \frac{d^2\phi }{d{t}^2}=-\frac{g}{R}\left(\cos \phi -{\mu }_k\sin \phi \right)-{\mu }_k{\left(\frac{d\phi }{dt}\right)}^2}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las condiciones iniciales siguientes: en el instante t=t₁, φ=θ₁, dφ/dt=(dθ/dt)₁

La ecuación de la dinámica de rotación alrededor de un eje que pasa por el c.m. es la misma que en el apartado anterior.

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=-F_{r}R{I}_c=\frac{2}{5}m{R}^2}$

Se resuelve la ecuación diferencial del movimiento del c.m. y obtenemos la función φ(t). Calculamos el valor de la fuerza de rozamiento en cada instante t mediante

${\displaystyle F_r=mR\frac{d^2\phi }{d{t}^2}+mg\cos \phi }$

Resolvemos aplicando procedimientos numéricos la ecuación del movimiento de rotación alrededor de un eje que pasa por el c.m. con las siguientes condiciones iniciales siguientes: en el instante t=t₁, θ=θ₁, dθ/dt=(dθ/dt)₁

Vigilamos el valor de la fuerza normal N

${\displaystyle N=mg\sin \phi -mR{\left(\frac{d\phi }{dt}\right)}^2}$

Cuando la fuerza normal N se anula, en el instante t₂, la posición del c.m. es

x₀=R·cos φ₂
y₀=R·sin φ₂

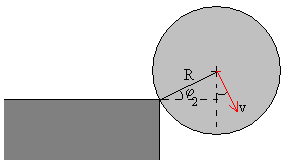
Las componentes rectangulares de la velocidad inicial del c.m. son:

${\displaystyle v_{0x}=R{\left(\frac{d\phi }{dt}\right)}_2\sin {\phi }_2{v}_{0y}=-R{\left(\frac{d\phi }{dt}\right)}_2\cos {\phi }_2}$

La velocidad angular final de rotación de la bola alrededor de un eje que pasa por el c.m. es (dθ/dt)₂

Tercera etapa del movimiento

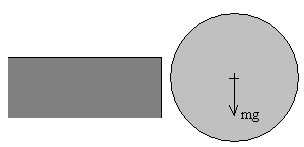
A partir del instante t₂, la bola cae libremente bajo la acción del peso actuando en el c.m. El c.m. de la bola describe un movimiento parabólico, a la vez que la bola gira con velocidad angular constante alrededor de un eje que pasa por el c.m.

${\displaystyle \begin{array}{l}x=R·\cos {\phi }_2+v_{0x}(t-t_2)\\ y=R·\sin {\phi }_2+v_{0y}(t-t_2)+\frac{1}{2}(-g){\left(t-t_2\right)}^2\\ \theta ={\theta }_2+{\left(\frac{d\theta }{dt}\right)}_2(t-t_2)\end{array}}$

Actividades

Se introduce

• El coeficiente de rozamiento, μ_k= μ_s en el control titulado Coef. rozamiento
• La velocidad inicial del c.m. de la bola, en el control titulado Velocidad inicial.
• El radio de la bola se ha fijado en R=1.0 m

Se pulsa el botón titulado Nuevo

Observamos las tres etapas del movimiento de la bola:

• Rotación alrededor de un eje que pasa por el borde de la mesa hasta el instante t₁ tal que θ=θ₁.
• Deslizamiento de la bola a lo largo del borde, hasta el instante t₂ en el que N=0
• Caída libre, el c.m. sigue una trayectoria parabólica a la vez que la bola describe un movimiento de rotación con velocidad angular constante alrededor de un eje que pasa por el c.m.

El programa nos proporciona, los datos de la posición del c.m. y de la velocidad angular de rotación.

Referencias

Bacon M. E.,How balls roll off tables. Am. J. Phys. 73 (8) August 2005, pp. 722-724