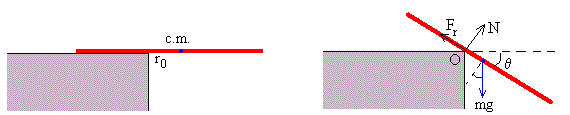
Las fuerzas que actúan sobre la tabla son:

• El peso, mg
• La fuerza que ejerce la mesa sobre la tabla, la fuerza normal N
• La fuerza de rozamiento entre el borde de la mesa y la tabla, F_r

El peso actuando en el centro de masas proporciona el momento que provoca el movimiento de rotación, mientras que la fuerza de rozamiento evita el deslizamiento de la tabla hasta el momento que alcanza un ángulo crítico. A partir de ese momento, la tabla desliza sobre el borde, hasta que la reacción N se hace cero. Finalmente, la tabla cae bajo la acción de su peso. Calcularemos para esta etapa del movimiento la velocidad inicial del centro de masas y la velocidad angular inicial de rotación alrededor de un eje que pasa por el c.m..

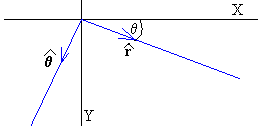
Utilizaremos las coordenadas polares para describir el movimiento de la tabla. Adoptaremos el sistema de referencia mostrado en la figura, con el eje Y apuntando hacia abajo.

Primera etapa del movimiento

Movimiento de rotación alrededor del borde, la distancia r del c.m.de la tabla al bode se mantiene constante e igual a la distancia inicial r₀.

Las ecuaciones del movimiento en la dirección radial $\widehat{r}$ y en la dirección $\widehat{\theta }$ son, respectivamente,

${\displaystyle \begin{array}{l}-m{r}_0{\left(\frac{d\theta }{dt}\right)}^2=mg\sin \theta -F_r\\ m{r}_0\frac{d^2\theta }{d{t}^2}=mg\cos \theta -N\end{array}}$

La ecuación de la dinámica de rotación alrededor del eje fijo O que pasa por el borde de la mesa, es

${\displaystyle I_O\frac{d^2\theta }{d{t}^2}=mg{r}_0\cos \theta I_O=\frac{1}{12}m{L}^2+m{r}_0^2}$

Integramos esta ecuación, con las condiciones iniciales siguientes: r=r₀, θ=0, ω=dθ/dt=0.

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=\frac{mg{r}_0\cos \theta }{I_O}\\ \frac{d\omega }{d\theta }\frac{d\theta }{dt}=\frac{mg{r}_0\cos \theta }{I_O}\omega \frac{d\omega }{d\theta }=\frac{mg{r}_0\cos \theta }{I_O}\\ {\displaystyle \underset{0}{\overset{\omega }{\int }}\omega ·d\omega =}\frac{mg{r}_0}{I_O}{\displaystyle \underset{0}{\overset{\theta }{\int }}\cos \theta ·d\theta }\\ \frac{1}{2}{\omega }^2=\frac{mg{r}_0}{I_O}\sin \theta \\ \left(\frac{d\theta }{dt}\right)=\sqrt{\frac{2mg{r}_0}{I_O}\sin \theta }\end{array}}$

Calculamos la reacción del borde N y la fuerza de rozamiento F_r

${\displaystyle \begin{array}{l}N=mg\cos \theta \left(1-\frac{m{r}_0^2}{I_O}\right)=\frac{L^2}{L^2+12r_0^2}mg\cos \theta \\ F_r=mg\sin \theta \left(1+\frac{2m{r}_0^2}{I_O}\right)=\frac{L^2+36r_0^2}{L^2+12r_0^2}mg\sin \theta \end{array}}$

La fuerza de rozamiento F_r va creciendo a medida que se incrementa el ángulo θ, hasta que alcanza el valor máximo μ_sN momento en el que la tabla empieza a deslizar sobre el borde. μ_s es el coeficiente estático de rozamiento. El ángulo crítico θ₁ para el cual F_r= μ_sN es

${\displaystyle \tan {\theta }_1={\mu }_s\frac{L^2}{L^2+36r_0^2}}$

Para calcular el ángulo que gira la tabla en función del tiempo hay que resolver la ecuación diferencial por procedimientos numéricos

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{mg{r}_0\cos \theta }{I_O}}$

con las siguientes condiciones iniciales: en el instante t=0, θ=0, dθ/dt=0. Se termina la primera etapa del movimiento en el instante t₁ cuando la tabla forma un ángulo θ₁ por debajo de la horizontal y lleva una velocidad angular.

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_1=\sqrt{\frac{2mg{r}_0}{I_O}\sin {\theta }_1}=\sqrt{\frac{24g{r}_0}{L^2+12r_0^2}\sin {\theta }_1}}$

Ejemplo.

• Sea una tabla de L=10.2 cm
• El coeficiente de rozamiento estático es μ_s=0.3
• El centro de masas está inicialmente a una distancia r₀= 0.55 cm del borde de la mesa

El ángulo girado por la tabla al concluir la primera etapa del movimiento y la velocidad angular de rotación valen, respectivamente,

${\displaystyle \begin{array}{l}\tan {\theta }_1=0.3\frac{{0.102}^2}{{0.102}^2+36·{0.0055}^2}{\theta }_1=15.2º\\ {\left(\frac{d\theta }{dt}\right)}_1=\sqrt{\frac{24·9.8·0.0055}{{0.102}^2+12·{0.0055}^2}\sin {\theta }_1}=5.61\text{rad/s}\end{array}}$

Segunda etapa del movimiento

En este caso, la distancia r del borde de la mesa al c.m. de la tabla cambia con el tiempo. La tabla continuará girando.

Las ecuaciones del movimiento en la dirección radial $\widehat{r}$ y en la dirección $\widehat{\theta }$ son, respectivamente,

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=mg\sin \theta -F_r\\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=mg\cos \theta -N\end{array}}$

La ecuación de la dinámica de rotación respecto al eje que pasa por el punto O no es correcta ya que ha dejado de estar en reposo respecto de un sistema de referencia inercial, tendremos que usar la ecuación

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N·r{I}_c=\frac{1}{12}m{L}^2}$

referida al eje que pasa por el c.m.que es válida incluso si el centro de masas (c.m.) no está en reposo con relación al sistema inercial.

Como la tabla está deslizando, la relación entre la fuerza de rozamiento y la fuerza normal es

F_r=μ_k·N

Donde μ_k es el coeficiente cinético de rozamiento

En el sistema de ecuaciones despejamos d²r/dt² y d²θ/dt²

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}=\frac{12r}{L^2+12r^2}\left(g\cos \theta -2\frac{dr}{dt}\frac{d\theta }{dt}\right)\\ \frac{d^{2}r}{d{t}^2}=g\sin \theta +r{\left(\frac{d\theta }{dt}\right)}^2-\frac{{\mu }_k{L}^2}{L^2+12r^2}\left(g\cos \theta -2\frac{dr}{dt}\frac{d\theta }{dt}\right)\end{array}}$

Resolvemos este sistema de ecuaciones diferenciales por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=t₁, r=r₀, dr/dt=0, y

${\displaystyle {\theta }_1=\arctan \left({\mu }_s\frac{L^2}{L^2+36r_0^2}\right){\left(\frac{d\theta }{dt}\right)}_1=\sqrt{\frac{24g{r}_0}{L^2+12r_0^2}\sin {\theta }_1}}$

Vigilamos el valor de la fuerza normal N

${\displaystyle N=\frac{m{L}^2}{12r}\frac{d^2\theta }{d{t}^2}}$

Cuando la fuerza normal N sea nula, en el instante t₂, la posición del c.m. en coordenadas polares es (r₂, θ₂) y sus velocidades son (dr/dt)₂ y (dθ/dt)₂

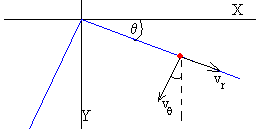
Las componentes rectangulares de la velocidad del c.m. son:

${\displaystyle \begin{array}{l}{v}_{0x}=v_r\cos {\theta }_2-v_{\theta }\sin {\theta }_2={\left(\frac{dr}{dt}\right)}_2\cos {\theta }_2-r_2{\left(\frac{d\theta }{dt}\right)}_2\sin {\theta }_2\\ v_{0y}=v_r\sin {\theta }_2+v_{\theta }\cos {\theta }_2={\left(\frac{dr}{dt}\right)}_2\sin {\theta }_2+r_2{\left(\frac{d\theta }{dt}\right)}_2\cos {\theta }_2\end{array}}$

La velocidad angular final de rotación de la tabla alrededor de un eje que pasa por el c.m. es (dθ/dt)₂

Tercera etapa del movimiento

A partir del instante t₂, la tabla cae libremente bajo la acción del peso actuando en el c.m. El c.m. de la tabla describe un movimiento parabólico, a la vez que la tabla gira con velocidad angular constante alrededor de un eje que pasa por el c.m.

${\displaystyle \begin{array}{l}x=r_2·\cos {\theta }_2+v_{0x}(t-t_2)\\ y=r_2·\sin {\theta }_2+v_{0y}(t-t_2)+\frac{1}{2}g{\left(t-t_2\right)}^2\\ \theta ={\theta }_2+{\left(\frac{d\theta }{dt}\right)}_2(t-t_2)\end{array}}$

Actividades

Se introduce

• La distancia inicial r₀ entre el centro de masas y el borde de la mesa, en el control titulado Distancia.
• El coeficiente de rozamiento, μ_k= μ_s en el control titulado Coef. rozamiento
• La longitud de la tabla se ha fijado en L=10.2 cm
• Se pulsa el botón titulado Nuevo

Observamos las tres etapas del movimiento de la tabla:

1. Rotación alrededor de un eje que pasa por el borde de la mesa hasta el instante t₁ tal que θ=θ₁.
2. Deslizamiento de la tabla a lo largo del borde, hasta el instante t₂ en el que N=0
3. Caída libre, el c.m. sigue una trayectoria parabólica a la vez que la tabla describe un movimiento de rotación con velocidad angular constante alrededor de un eje que pasa por el c.m.

El programa nos proporciona, los datos de la posición del c.m. y de la velocidad angular de rotación

Una varilla desliza y gira sobre una barandilla

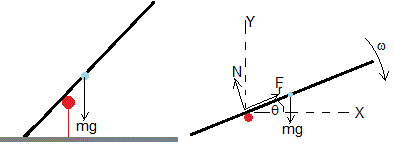
Las barandillas (punto de color rojo) suelan tener una altura mayor que la del centro de masa (azul claro) de una persona, para evitar que caiga por la acción del momento de su peso

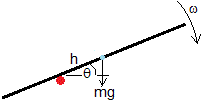
Una varilla de masa m y longitud l que hace una ángulo θ con la horizontal está apoyada en la barandilla con el centro de masa a una distancia h por encima.

mg es el peso, N es la reacción de la barandilla y F_r la fuerza de rozamiento entre la varilla y el apoyo.

• si |F_r|≥μ_sN la varilla desliza y (gira), la fuerza de rozamiento será F_r=μ_kN de módulo y de sentido contario a la velocidad con la que se desplaza la varilla

• si |F_r|<μ_sN, la varilla gira alrededor de la barandilla

Ecuaciones del movimiento

• Traslación del centro de masas de la varilla

${\displaystyle \begin{array}{l}m\frac{d{v}_x}{dt}=F_r\cos \theta -N\sin \theta \\ m\frac{d{v}_y}{dt}=F_r\sin \theta +N\cos \theta -mg\end{array}}$

• Rotación de la varilla alrededor de un eje perpendicular que pasa por el c.m.

${\displaystyle I_{cm}\frac{d^2\theta }{d{t}^2}=-Nh,I_{cm}=\frac{1}{12}m{l}^2}$

La posición del centro de masa es

${\displaystyle \{\begin{array}{l}x=h\cos \theta \\ y=h\sin \theta \end{array}}$

Derivamos con respecto del tiempo

${\displaystyle \{\begin{array}{l}{v}_x=\frac{dx}{dt}=\frac{dh}{dt}\cos \theta -h\sin \theta \frac{d\theta }{dt}\\ v_y=\frac{dy}{dt}=\frac{dh}{dt}\sin \theta +h\cos \theta \frac{d\theta }{dt}\end{array}}$

Derivamos de nuevo, respecto del tiempo

${\displaystyle \{\begin{array}{l}\frac{d{v}_x}{dt}=\frac{d^{2}h}{d{t}^2}\cos \theta -2\frac{dh}{dt}\sin \theta \frac{d\theta }{dt}-h\cos \theta {\left(\frac{d\theta }{dt}\right)}^2-h\sin \theta \frac{d^2\theta }{d{t}^2}\\ \frac{d{v}_y}{dt}=\frac{d^{2}h}{d{t}^2}\sin \theta +2\frac{dh}{dt}\cos \theta \frac{d\theta }{dt}-h\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+h\cos \theta \frac{d^2\theta }{d{t}^2}\end{array}}$

En el sistema de ecuaciones, despejamos N y F_r

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{F_r}{m}\cos \theta -\frac{N}{m}\sin \theta =\frac{d^{2}h}{d{t}^2}\cos \theta -2\sin \theta \frac{dh}{dt}\frac{d\theta }{dt}-h\cos \theta {\left(\frac{d\theta }{dt}\right)}^2-h\sin \theta \frac{d^2\theta }{d{t}^2}\\ \frac{F_r}{m}\sin \theta +\frac{N}{m}\cos \theta -g=\frac{d^{2}h}{d{t}^2}\sin \theta +2\cos \theta \frac{dh}{dt}\frac{d\theta }{dt}-h\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+h\cos \theta \frac{d^2\theta }{d{t}^2}\end{array}\\ \frac{F_r}{m}-g\sin \theta =\frac{d^{2}h}{d{t}^2}-h{\left(\frac{d\theta }{dt}\right)}^2\\ \frac{N}{m}-g\cos \theta =2\frac{dh}{dt}\frac{d\theta }{dt}+h\frac{d^2\theta }{d{t}^2}\end{array}}$

Sustituimos d²θ/dt² de la ecuación de la dinámica de rotación de la varilla

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{F_r}{m}=g\sin \theta +\frac{d^{2}h}{d{t}^2}-h{\left(\frac{d\theta }{dt}\right)}^2\\ \frac{N}{m}=g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}-\frac{N{h}^2}{I_{cm}}\end{array}\\ \{\begin{array}{l}\frac{F_r}{m}=g\sin \theta +\frac{d^{2}h}{d{t}^2}-h{\left(\frac{d\theta }{dt}\right)}^2\\ \frac{N}{m}\left(1+\frac{h^2}{\frac{1}{12}{l}^2}\right)=g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}\end{array}\end{array}}$

• La varilla no desliza, |F_r|<μ_sN, la varilla gira alrededor de la barandilla

La distancia h es fija y dh/dt=0

${\displaystyle \begin{array}{l}\frac{N}{m}=l^2\frac{g\cos \theta }{l^2+12h^2}\\ I_{cm}\frac{d^2\theta }{d{t}^2}=-Nh\\ \frac{1}{12}{l}^2\frac{d^2\theta }{d{t}^2}=-l^2\frac{gh\cos \theta }{l^2+12h^2}\\ \frac{d^2\theta }{d{t}^2}=-\frac{gh\cos \theta }{\frac{1}{12}{l}^2+h^2}\end{array}}$



que es la ecuación del movimiento de rotación de la varilla alrededor del punto de apoyo

${\displaystyle \left(\frac{1}{12}m{l}^2+m{h}^2\right)\frac{d^2\theta }{d{t}^2}=-mgh\cos \theta }$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales θ=θ₀, dθ/dt=(dθ/dt)₀

• La varilla desliza sobre la barandilla y gira. La fuerza de rozamiento F_r=μ_kN, de módulo y sentido contrario a la velocidad con la que se desplaza la varilla sobre el apoyo -(dh/dt)

${\displaystyle \begin{array}{l}\{\begin{array}{l}g\sin \theta +\frac{d^{2}h}{d{t}^2}-h{\left(\frac{d\theta }{dt}\right)}^2=-\frac{{\mu }_k}{1+\frac{12h^2}{l^2}}\mathrm{sgn}\left(\frac{dh}{dt}\right)\left(g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}\right)\\ \frac{1}{12}m{l}^2\frac{d^2\theta }{d{t}^2}=-m{l}^2\frac{g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}}{l^2+12h^2}h\end{array}\\ \{\begin{array}{l}\frac{d^{2}h}{d{t}^2}=-\frac{{\mu }_k{l}^2}{l^2+12h^2}\mathrm{sgn}\left(\frac{dh}{dt}\right)\left(g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}\right)-g\sin \theta +h{\left(\frac{d\theta }{dt}\right)}^2\\ \frac{d^2\theta }{d{t}^2}=-h\frac{g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}}{\frac{1}{12}{l}^2+h^2}\end{array}\end{array}}$

Se resuelve el sistema de ecuaciones diferenciales, con las condiciones iniciales h=h₀, dh/dt=0, θ=θ₀, dθ/dt=(dθ/dt)₀

El término sgn(dh/dt) significa signo de la velocidad de desplazamiento del centro de masas de la varilla respecto del punto de apoyo

Pasos del cálculo

La varilla parte del reposo dθ/dt=0, inclinada un ángulo θ₀, su centro de masas dista h del punto de apoyo, la fuerza de rozamiento F_r y la normal N valen

${\displaystyle \begin{array}{l}\frac{N}{m}=l^2\frac{g\cos \theta }{l^2+12h^2}\\ \frac{F_r}{m}=g\sin \theta \end{array}}$

1. Supongamos que |F_r|<μ_sN la varilla solamente gira, (la distancia h es constante) se resuelve la primera ecuación diferencial

En cada instante se calcula F_r y N y se comparan

${\displaystyle \{\begin{array}{l}\frac{F_r}{m}=g\sin \theta -h{\left(\frac{d\theta }{dt}\right)}^2\\ \frac{N}{m}=\frac{g\cos \theta }{1+\frac{12h^2}{l^2}}\end{array}}$

2. Cuando |F_r|>μ_sN, la varilla desliza y gira, se resuelve el sistema de dos ecuaciones diferenciales con las condiciones iniciales iguales a las finales de la etapa anterior

3. La varilla puede detenerse, en cuyo caso se calcula la reacción N y la fuerza de rozamiento F_r con la distancia h constante. Comienza un nuevo ciclo de cálculo

4. Cuando la reacción N se anula, la simulación termina.

${\displaystyle \frac{N}{m}=\frac{g\cos \theta +2\frac{dh}{dt}\frac{d\theta }{dt}}{1+\frac{12h^2}{l^2}}}$

El movimiento posterior, sería el de una varilla cuyo centro de masa cae con aceleración de la gravedad a la vez que gira.

Resultados

Representamos la velocidad angular dθ/dt en función del tiempo t, de una varilla de l=185 mm de largo que se suelta cuando hace un ángulo θ=0. La distancia inicial h del punto de apoyo al centro de masas se va cambiando, 20, 10, 5 y 1 mm. El coeficiente de rozamento μ=0.2

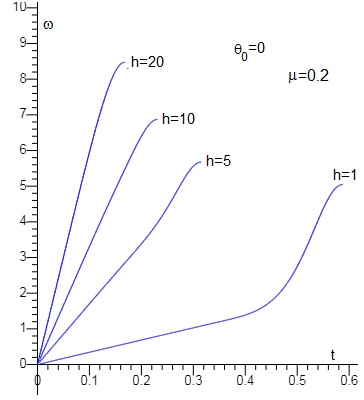
Lo mismo para una varilla que se suelta cuando hace 30° con la horizontal. La distancia inicial h del punto de apoyo al centro de masas se va cambiando, 30, 20 y 10 mm

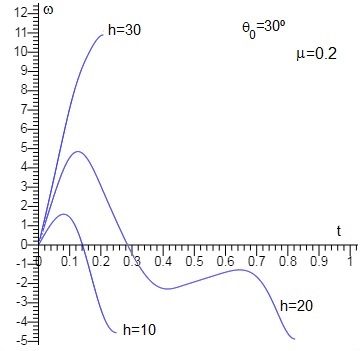
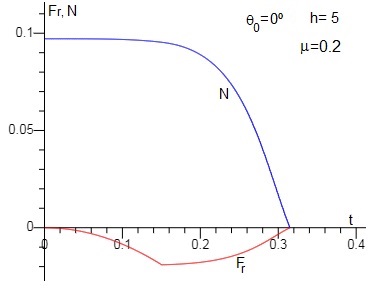
Representamos la fuerza de rozamiento F_r (rojo) y la reacción N (azul) en función del tiempo t, de la varilla que se suelta cuando hace un ángulo θ=0°. La distancia inicial del punto de apoyo al centro de masas es h=5 mm.

Coinciden con la figura 4 del artículo de Cross

Lo mismo cuando la varilla forma un ángulo inicial de 30°, distancia inicial h=20 mm

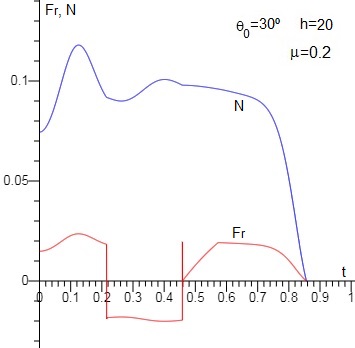
Coinciden cualitativamente con la figura 5 del artículo de Cross

Actividades

Se introduce

• El ángulo inicial θ₀ que forma la varilla con la horizontal
• La distancia inicial h entre el apoyo y el centro de masas

Se ha fijado el coeficiente μ=μ_k=μ_s=0.2.

A la izquierda, se observa el movimiento de la varilla, a la derecha, representamos en color azul la reacción N y en color rojo, la fuerza de rozamiento F_r en función del tiempo.

A la izquierda se proporcionan los datos de

• El tiempo t en s
• El ángulo que forma la varilla con la horizontal, θ en grados
• la distancia h entre el punto de apoyo y el centro de masas, en mm
• La velocidad de desplazamiento dh/dt del centro de masas, en mm/s
• La fuerza de rozamiento F_r/m
• La reacción μN/m en el punto de apoyo. Cuando el cuerpo desliza |F_r|=μN

Referencias

Steinert D. It’s not Murphy’s law, it’s Newton’s. The Physics Teacher Vol 34, May 1996, pp. 288-289

Bacon M. E., Heald G., James M. A closer look at tumbling toast. Am. J. Phys. 69 (1) January 2001, pp. 38-43

Rod Cross. Falling off a balcony: a student experiment. Eur. J. Phys. 44 (2023) 055005