Consideremos la colisión elástica entre una bola de masa m incidente con velocidad v₀ contra otra bola de masa M que está en reposo.

• Por la conservación del momento lineal

mv₀=mv+MV

• Por la conservación de la energía

${\displaystyle \frac{1}{2}m{v}^2+\frac{1}{2}M{V}^2=\frac{1}{2}m{v}_0^2}$

La solución de este sistema de dos ecuaciones con dos incógnitas es

${\displaystyle \{\begin{array}{l}v=\frac{m-M}{m+M}{v}_0\\ V=\frac{2m}{m+M}{v}_0\end{array}}$

Cundo las bolas son idénticas M=m, v=0, y V=v₀. La primera bola permenece en reposo después del choque. Hay un intercambio de momento lineal, la primera se lo cede a la segunda, quedando aquella en reposo.

La teoría de la colisión elástica entre dos esferas se debe a H. Hertz y se explica en el Volumen 7 del Curso de Física Teórica de Landau y Lifshitz. La conclusión es que la ley de de la fuerza de interacción no es lineal

${\displaystyle F=k{x}^{3/2}}$

donde k está relacionado con el módulo del Young, el coeficiente de Poisson del material elástico y el radio de la esfera y x es la deformación

Experiencia

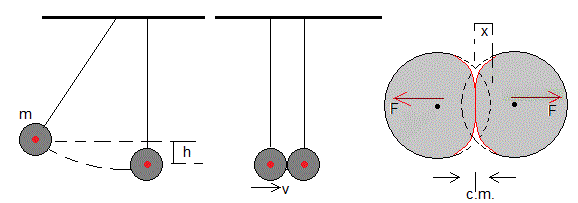
Sean dos esferas idénticas de masa m, cuando están en reposo, las dos esferas están en contacto y la línea que une sus centros es horizontal. Se desvía una de las esferas de su posición de equilibrio, de modo que su centro se eleva una altura h. Se suelta y a continuación, choca con la esfera en reposo. La velocidad de la esfera antes del choque es

${\displaystyle \frac{1}{2}m{v}^2=mgh}$

La velocidad del centro de masas de ambas esferas iguales es v/2. La velocidad de cada una de las esferas relativa al centro de masas es v/2 y de sentido contrario. Este Sistema de Referencia del c.m. es el adecuado para describir el choque de las dos esferas y la deformación de las mismas.

La energía cinética relativa al c.m. de cada una de las esferas antes del choque es

${\displaystyle E_k=\frac{1}{2}m{\left(\frac{v}{2}\right)}^2=\frac{1}{4}mgh}$

La energía cinética del c.m. es

${\displaystyle E_{cm}=\frac{1}{2}2m{\left(\frac{v}{2}\right)}^2=\frac{1}{2}mgh}$

La energía total, suma de la energía cinética de cada una de las dos esferas relativas al c.m. y la energía cinética del c.m. es mgh

Supondremos que los cuerpos deformados (véase la figura a la derecha) se comportan como muelles no lineales cuyo comportamiento se describe por una ley de fuerza F=-kx^n-1. La energía potencial correspondiente a esta fuerza conservativa es

${\displaystyle \begin{array}{l}{E}_p(0)-E_p(x)={\displaystyle \underset{0}{\overset{x}{\int }}-k{x}^{n-1}dx}\\ E_p(x)=\frac{k}{n}{x}^n\end{array}}$

Se supone que cuando las esferas no se han deformado x=0, E_p(x)=0. El principio de conservación de la energía para cada una de las esferas cuando se han deformado x se escribe

${\displaystyle \frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{k}{n}{x}^n=E_k}$

La máxima deformación x₀ se obtiene cuando la velocidad es nula dx/dt=0.

${\displaystyle \frac{k}{n}{x}_0^n=E_k}$

Duración del choque

Integramos la ecuación diferencial para calcular la duración del choque T, el doble desde que las esferas entran en contacto x=0 hasta que alcanzan la máxima deformación x=x₀.

${\displaystyle \begin{array}{l}t(x)={\displaystyle \underset{0}{\overset{t}{\int }}dt}=\sqrt{\frac{m}{2}}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{\sqrt{E_k-\frac{k}{n}{x}^n}}}\\ t(x)=\sqrt{\frac{m}{2E_k}}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{\sqrt{1-\frac{k{x}^n/n}{k{x}_0^n/n}}}}\end{array}}$

Definimos una nueva variable z, tal que x=z·x₀, de modo que cuando x varía entre 0 y x₀, z varía entre 0 y 1

${\displaystyle t(z)=x_0\sqrt{\frac{2}{gh}}{\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{1-z^n}}}}$

La duración T de choque es

${\displaystyle \begin{array}{l}T=2x_0\sqrt{\frac{2}{gh}}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{1-z^n}}}\\ T=2{\left(\frac{1}{4}mgh\frac{n}{k}\right)}^{1/n}\sqrt{\frac{2}{gh}}\gamma \\ T=\sqrt{\frac{8}{g}}\gamma {\left(\frac{nmg}{4k}\right)}^{1/n}{h}^{(2-n)/2n}\end{array}}$

Esta es la relación entre la duración del choque T y la altura inicial h de la esfera que impacta. El parámetro γ guarda el valor de la integral definida de entre 0 y 1

Se mide la duración del choque T para varias alturas h de la esfera que impacta, se ajustan los datos experimentales mediante el procedimiento de mínimos cuadrados para obtener el exponente n de la ley de fuerza y la constante k.

En la experiencia que se describe en el artículo mencionado en las referencias, se han utilizado una esfera de acero de masa m=225.8 g, obteniéndose un exponente de la ley de fuerza n-1=2.51-1≈3/2 y una constante k=4.553·10¹⁰ kg/m^(3/2).

Impulso

Vamos a dibujar la función F(t), fuerza en función del tiempo t para una altura h determinada. Calcularemos el impulso y lo compararemos con la variación de momento lineal.

Dado h calculamos la máxima deformación x₀

${\displaystyle x_0={\left(\frac{1}{4}mgh\frac{n}{k}\right)}^{1/n}}$

Para cada z_i=x_i/x₀, i=1...N, comprendidos entre 0 y 1 calculamos la fuerza F_i

${\displaystyle F_i=k{x}_i^{n-1}=k{x}_0^{n-1}{z}_i^{n-1}}$

Para cada z_i calculamos el tiempo t_i

${\displaystyle t_i=x_0\sqrt{\frac{2}{gh}}{\displaystyle \underset{0}{\overset{z_i}{\int }}\frac{dz}{\sqrt{1-z^n}}}}$

Hemos calculado la mitad de la curva F(t) desde 0 hasta el tiempo T/2. La otra mitad es simétrica

Representamos la fuerza F(t), en N dividida entre 1000, en función del tiempo, desde t=0 hasta t=T en µs,

m=0.2258; %masa esfera
k=4.553e10; %constante elástica
n=2.51; %exponente de la ley de fuerza

h=0.12; %altura
x0=(m*9.8*h*n/(4*k))^(1/n);
z1=linspace(0,1,200);
fuerza=k*(x0*z1).^(n-1);
t=zeros(1,length(z1));
i=1;
f=@(x) 1./sqrt(1-x.^n);
for z=z1
  t(i)=x0*sqrt(2/(9.8*h))*integral(f,0,z);
  i=i+1;
end
tt=[t,2*t(end)-flip(t)]/1e-6; %en micro segundos
ff=[fuerza,flip(fuerza)]/1000; 
plot(tt,ff);
grid on
xlabel('t (\mus)')
ylabel('F (N)/1000')
title('Fuerza en función del tiempo')

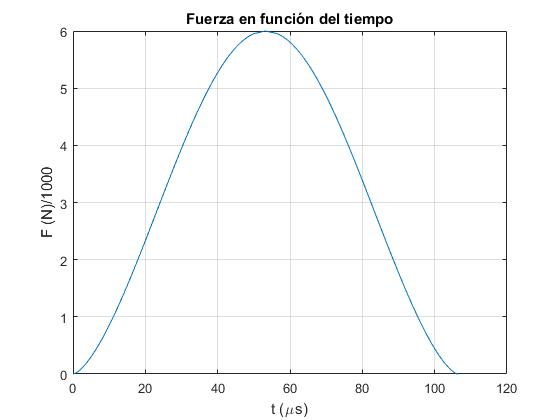
La duración del choque es de 106.5 µs y la máxima deformación x₀=2.78·10^-5 m

>> tt(end)
ans =  106.4796
>> x0
x0 =   2.7772e-05

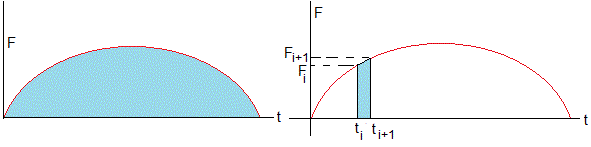
Calculamos el impulso, la integral definida para una función F(t). En este caso, para una tabla de datos, la suma de las áreas de los trapecios

${\displaystyle I={\displaystyle \underset{0}{\overset{T}{\int }}F(t)dt}}$

>> trapz(tt,ff)/1000
ans =    0.3462

En una colisión elástica, como hemos explicado al principio de esta página, la esfera que impacta se detiene después del choque. La variación de momento lineal es

${\displaystyle \Delta p=mv=m\sqrt{2gh}}$

>> m*sqrt(2*9.8*h)
ans =    0.3463

Comprobamos que el impulso de la fuerza F(t) que actúa durante un tiempo T sobre la esfera que impacta, es igual a la variación de su momento lineal

Referencias

R. Hessel, A. C. Perinotto, R. A. M. Alfaro, A. A. Freschi. Force-versus-time curves during collisions between two identical steel balls. Am. J. Phys. 74 (3) march 2006, pp. 176-179

Landau L. D., Lifshitz E. M. Teoría de la elasticidad. Edt. Reverté, (1969), pp. 42-4