En la página titulada Modos normales de vibración (I), calculamos las frecuencias de los modos normales de vibración de un sistema formado por n partículas unidas a n+1 muelles

Las ecuaciones del movimiento en forma matricial son

${\displaystyle \left(\begin{array}{cccccc}{m}_1& 0& 0& 0& \mathrm{...}& 0\\ 0& m_2& 0& 0& \mathrm{...}& 0\\ 0& 0& m_3& 0& \mathrm{...}& 0\\ 0& 0& 0& m_4& \mathrm{..}& 0\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 0& 0& 0& 0& \mathrm{...}& m_n\end{array}\right)\frac{d^2}{d{t}^2}\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ \mathrm{...}\\ x_n\end{array}\right)+\left(\begin{array}{cccccc}(k_1+k_2)& -k_2& 0& 0& \mathrm{...}& 0\\ -k_2& (k_2+k_3)& -k_3& 0& \mathrm{...}& 0\\ 0& -k_3& (k_3+k_4)& -k_4& \mathrm{...}& 0\\ 0& 0& -k_4& (k_4+k_5)& \mathrm{..}& 0\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 0& 0& 0& 0& \mathrm{...}& (k_n+k_{n+1})\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ \mathrm{...}\\ x_n\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ \mathrm{...}\\ 0\end{array}\right)}$

Vamos a estudiar el caso particular de un sistema formado por n/2 pares de partículas de masa m. Las dos partículas están unidas por muelles de constante k (en color azul). Los pares están unidos por muelles de constante g (en color rojo)

Dos pares de partículas, n=4

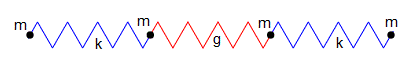
En este caso, m₁=m₂=m₃=m₄=m

k₁=0, k₂=k, k₃=g, k₄=k, k₅=0

${\displaystyle \left(\begin{array}{cccc}m& 0& 0& 0\\ 0& m& 0& 0\\ 0& 0& m& 0\\ 0& 0& 0& m\end{array}\right)\frac{d^2}{d{t}^2}\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)+\left(\begin{array}{cccc}k& -k& 0& 0\\ -k& k+g& -g& 0\\ 0& -g& g+k& -k\\ 0& 0& -k& k\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right)}$

La matriz M de las masas es

${\displaystyle {\rm M}=\left(\begin{array}{cccc}m& 0& 0& 0\\ 0& m& 0& 0\\ 0& 0& m& 0\\ 0& 0& 0& m\end{array}\right)}$

La matriz K de las constantes de los muelles es

${\displaystyle K=\left(\begin{array}{cccc}k& -k& 0& 0\\ -k& k+g& -g& 0\\ 0& -g& g+k& -k\\ 0& 0& -k& k\end{array}\right)}$

Las frecuencias de los modos normales de vibración se calculan resolviendo el sistema homogéneo

${\displaystyle \begin{array}{l}-{\omega }^{2}M·x+K·x=0\hfill \\ \begin{array}{l}(K-{\omega }^{2}mI)·x=0\\ (K-\lambda I)·x=0\end{array}\hfill \end{array}}$

Calculamos los valores propios de la matriz K

${\displaystyle \left|\begin{array}{cccc}k-\lambda & -k& 0& 0\\ -k& \left(k+g\right)-\lambda & -g& 0\\ 0& -g& \left(k+g\right)-\lambda & -k\\ 0& 0& -k& k-\lambda \end{array}\right|=0}$

Conocidos los valores propios se determinan las frecuencias de los modos normales de vibración

${\displaystyle \omega =\sqrt{\frac{\lambda }{m}},f=\frac{1}{2\pi }\sqrt{\frac{\lambda }{m}}}$

La función eig devuelve la matriz D cuya diagonal contiene los cuatro valores propios λ

>> syms k g;
>> K=[k,-k,0,0;-k,k+g,-g,0;0,-g,g+k,-k; 0,0,-k,k];
>> [V,D]=eig(K)
D =
[0,   0,                         0,                         0]
[0, 2*k,                         0,                         0]
[0,   0, g + k + (g^2 + k^2)^(1/2),                         0]
[0,   0,                         0, g + k - (g^2 + k^2)^(1/2)]

${\displaystyle \begin{array}{l}{f}_1=0\\ f_2=\frac{1}{2\pi }\sqrt{\frac{2k}{m}}\\ f_3=\frac{1}{2\pi }\sqrt{\frac{g+k+\sqrt{g^2+k^2}}{m}}\\ f_4=\frac{1}{2\pi }\sqrt{\frac{g+k-\sqrt{g^2+k^2}}{m}}\end{array}}$

Tres pares de partículas, n=6

En este caso, m₁=m₂=m₃=m₄=m₅=m₆=m

k₁=0, k₂=k, k₃=g, k₄=k, k₅=g, k₆=k, k₇=0

La matriz K de las constantes de los muelles es

${\displaystyle K=\left(\begin{array}{cccccc}k& -k& 0& 0& 0& 0\\ -k& k+g& -g& 0& 0& 0\\ 0& -g& k+g& -k& 0& 0\\ 0& 0& -k& k+g& -g& 0\\ 0& 0& 0& -g& k+g& -k\\ 0& 0& 0& 0& -k& k\end{array}\right)}$

La matriz cuadrada K de dimensión n es simétrica y consta de una diagonal cuyos elementos son k+g, excepto el primero (1,1) y el último (n,n) que son k. En la diagonal adyaccente (i, i+1) i=1,2...n-1 se alternan los valores -k y -g. El código MATLAB para crear esta matriz es

g=1.7; %constante muelle que une pares de partículas
k=5.0; %constante del muelle que une dos partículas
n=6; %número de partículas
K=diag((k+g)*ones(1,n))+diag(-k*ones(1,n-1),1)+diag(-k*ones(1,n-1),-1);
K(1,1)=k;
K(n,n)=k;
for s=3:2:n
    K(s,s-1)=-g;
    K(s-1,s)=-g;
end   

Los valores propoios son los elementos de la matriz D devuelta por la función eig. Conocidos los valores propios de calculan las frecuencias

    [V,D]=eig(K);
    frec=real(sqrt(diag(D)/m)/(2*pi));

Resultados

Representmos las frecuencias de los modos normales de vibración de un sistema de n=4, 6, 8, 10...30 partículas. Para k=5.0 N/m, g=1.7 N/m siendo la masa de las patículas m=145 g

g=1.7; %constante muelle 
k=5.0; %constante muelle
m=145/1000; %masa partículas
hold on
for n=4:2:30 %número de partículas
    K=diag((k+g)*ones(1,n))+diag(-k*ones(1,n-1),1)+diag(-k*ones(1,n-1),-1);
    K(1,1)=k;
    K(n,n)=k;
    for s=3:2:n
        K(s,s-1)=-g;
        K(s-1,s)=-g;
    end   
    [V,D]=eig(K);
    frec=real(sqrt(diag(D)/m)/(2*pi));
    for s=1:n
        plot(n,frec(s),'ro','markersize',3,'markerfacecolor','r')
    end
end
hold off
grid on
xlabel('n')
ylabel('f (Hz)')
title('Frecuencias')

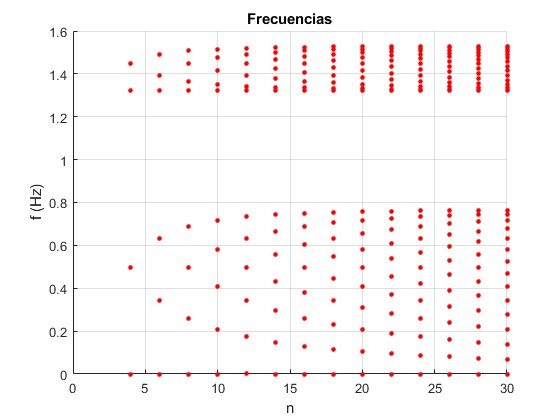
Una figura similar la encontramos al final de la página titulada Sistema de pozos de potencial

Representamos las frecuencias de los modos normales de vibración de un sistema de n=4 partículas, modificando la constante del muelle g que une los pares de partículas. La constante k=5 N/m

k=5.0; %muelles
m=145/1000; %masa partículas
n=4; %número de partículas
gg=linspace(0,5,100);
fr=zeros(length(gg),n);
j=1;
for g=gg
    K=diag((k+g)*ones(1,n))+diag(-k*ones(1,n-1),1)+diag(-k*ones(1,n-1),-1);
    K(1,1)=k;
    K(n,n)=k;
    for s=3:2:n
        K(s,s-1)=-g;
        K(s-1,s)=-g;
    end   
    [V,D]=eig(K);
    frec=real(sqrt(diag(D)/m)/(2*pi));
    for s=1:n
        fr(j,s)=frec(s);
    end
    j=j+1;
end
hold on
for s=1:n
    plot(gg,fr(:,s));
end

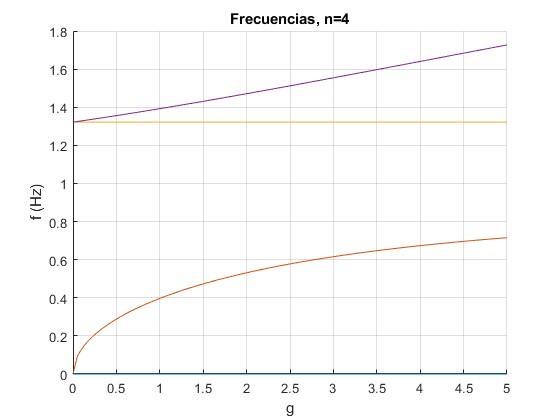
Cambiamos el número de partículas, n=8

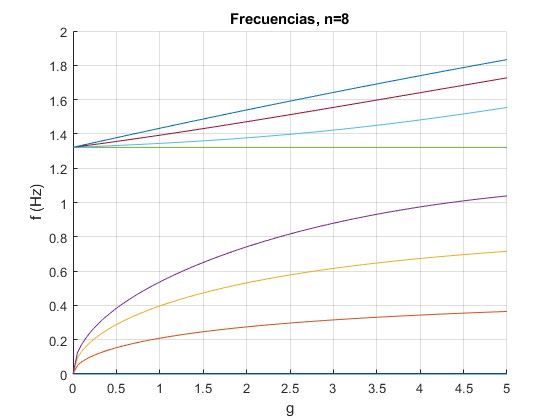
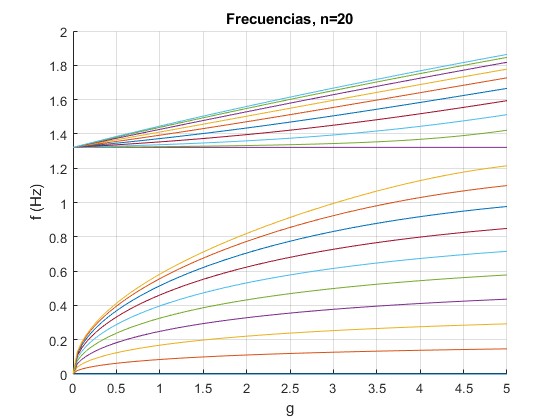
Cambiamos el número de partículas, n=20

Referencias

Parker Roberts, Alexandria Skinner, Tadan Cobb, Scott Carr, Shawn A. Hilbert. A classical analogy for quantum band formation. Am. J. Phys. 86 (8), August 2018. pp. 609-615