Osciladores acoplados en una circunferencia

Consideremos el sistema de la figura: n partículas de masa m, unidas por muelles de la misma constante k situados en una pista circular de radio R en la situación de equlibrio.

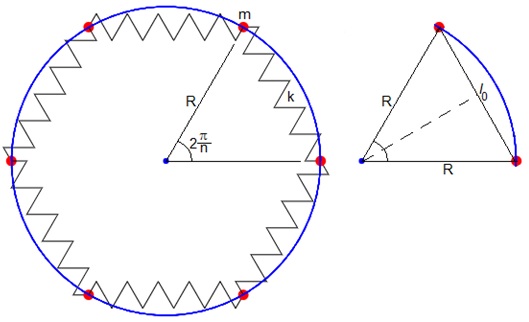
La distancia l₀ entre dos partículas consecutivas

$l_{0} = 2 R \sin (\frac{π}{n})$

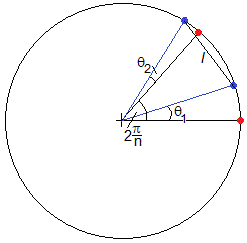
En el instante t la primera partícula se desplaza un ángulo θ₁, la segunda un ángulo θ₂ y así, sucesivamente. La distancia l entre dos partículas consecutivas (color azul) es

$l = 2 R \sin (\frac{1}{2} (θ_{2} - θ_{1} + \frac{2 π}{n}))$

La energía cinética y potencial del sistema de partículas es

$\begin{array}{l} E_{k} = \frac{1}{2} m {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m {(\frac{d θ_{2}}{d t})}^{2} + ... \frac{1}{2} m {(\frac{d θ_{n}}{d t})}^{2} \\ E_{p} = \frac{1}{2} k {(l_{1} - l_{0})}^{2} + \frac{1}{2} k {(l_{2} - l_{0})}^{2} + .... \frac{1}{2} k {(l_{n} - l_{0})}^{2} \end{array}$

Expresamos la energía potencial en términos de los desplazamientos angulares θ_i

$\begin{array}{l} l_{j} - l_{0} = 2 R \sin (\frac{1}{2} (θ_{j + 1} - θ_{j} + \frac{2 π}{n})) - 2 R \sin (\frac{π}{n}) = \\ 2 R \sin (\frac{θ_{j + 1} - θ_{j}}{2}) \cos (\frac{π}{n}) + 2 R \cos (\frac{θ_{j + 1} - θ_{j}}{2}) \sin (\frac{π}{n}) - 2 R \sin (\frac{π}{n}) \approx \\ R (θ_{j + 1} - θ_{j}) \cos (\frac{π}{n}) + 2 R \sin (\frac{π}{n}) - 2 R \sin (\frac{π}{n}) = R (θ_{j + 1} - θ_{j}) \cos (\frac{π}{n}) \end{array}$

La expresión aproximada de la energía potencial (amplitudes pequeñas) es

$\begin{array}{l} E_{p} \approx \frac{1}{2} k R^{2} \cos^{2} (\frac{π}{n}) {{(θ_{2} - θ_{1})}^{2} + {(θ_{3} - θ_{2})}^{2} + ... {(θ_{n + 1} - θ_{n})}^{2}} \\ E_{p} \approx \frac{1}{2} R^{2} k_{e} {{(θ_{2} - θ_{1})}^{2} + {(θ_{3} - θ_{2})}^{2} + ... {(θ_{1} - θ_{n})}^{2}}, k_{e} = k \cos^{2} (\frac{π}{n}) \end{array}$

Ahora bien, θ_n+1=θ_n por estar las partículas confinadas a moverse en una circunferencia. k_e=kcos²(π/n) es la constante efectiva de los muelles elásticos

La Lagrangiana de este sistema es

$L = E_{k} - E_{p} = R^{2} {\frac{1}{2} m {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m {(\frac{d θ_{2}}{d t})}^{2} + ... \frac{1}{2} m {(\frac{d θ_{n}}{d t})}^{2}} - \frac{1}{2} k_{e} R^{2} {{(θ_{2} - θ_{1})}^{2} + {(θ_{3} - θ_{2})}^{2} + ... {(θ_{1} - θ_{n})}^{2}}$

Las ecuaciones del movimiento de cada partícula

$\frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{j}}) - \frac{\partial L}{\partial θ_{j}} = 0$

Sistema de n=4 partículas

Consideremos un sistema de n=4 partículas de la misma masa m, conectadas por muelles elásticos de la misma constante k y obligadas a moverse por una pista circular de radio R

La lagrangiana es

$L = \frac{1}{2} m R^{2} {{(\frac{d θ_{1}}{d t})}^{2} + {(\frac{d θ_{2}}{d t})}^{2} + {(\frac{d θ_{3}}{d t})}^{2} + {(\frac{d θ_{4}}{d t})}^{2}} - \frac{1}{2} k_{e} R^{2} {{(θ_{2} - θ_{1})}^{2} + {(θ_{3} - θ_{2})}^{2} + {(θ_{4} - θ_{3})}^{2} + {(θ_{1} - θ_{4})}^{2}}$

Las ecuaciones del movimiento

$\begin{array}{l} m \frac{d^{2} θ_{1}}{d t^{2}} + k_{e} (2 θ_{1} - θ_{2} - θ_{4}) = 0 \\ m \frac{d^{2} θ_{2}}{d t^{2}} + k_{e} (2 θ_{2} - θ_{1} - θ_{3}) = 0 \\ m \frac{d^{2} θ_{3}}{d t^{2}} + k_{e} (2 θ_{3} - θ_{2} - θ_{4}) = 0 \\ m \frac{d^{2} θ_{4}}{d t^{2}} + k_{e} (2 θ_{4} - θ_{3} - θ_{1}) = 0 \end{array}$

En forma matricial

$\begin{array}{l} (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}) \frac{d^{2}}{d t^{2}} (\begin{matrix} θ_{1} \\ θ_{2} \\ θ_{3} \\ θ_{4} \end{matrix}) + \frac{k_{e}}{m} (\begin{matrix} 2 & - 1 & 0 & - 1 \\ - 1 & 2 & - 1 & 0 \\ 0 & - 1 & 2 & - 1 \\ - 1 & 0 & - 1 & 2 \end{matrix}) (\begin{matrix} θ_{1} \\ θ_{2} \\ θ_{3} \\ θ_{4} \end{matrix}) = 0 \\ I \frac{d^{2} θ}{d t^{2}} + \frac{k_{e}}{m} K θ = 0 \end{array}$

K es la matriz de las constantes de los muelles.

Valores propios

Buscamos una solución de la forma

θ₁=X₁sin(ωt+φ₁), θ₂=X₂sin(ωt+φ₂), θ₃=X₃sin(ωt+φ₃) y θ₄=X₄sin(ωt+φ₄)

que representan MAS de amplitud X₁, X₂, X₃ y X₄, frecuencia angular ω.

$\begin{array}{l} (- ω^{2} I + \frac{k_{e}}{m} K) X = 0 \\ (- ω^{2} \frac{m}{k_{e}} I + K) X = 0 \end{array}$

Tenemos un sistema homogéneo, los cuadrados de las frecuencias ω² de los modos normales de vibración se calculan haciendo que el determinante de los coeficientes sea igual a cero

$| \begin{matrix} 2 - λ & - 1 & 0 & - 1 \\ - 1 & 2 - λ & - 1 & 0 \\ 0 & - 1 & 2 - λ & - 1 \\ - 1 & 0 & - 1 & 2 - λ \end{matrix} | = 0, λ = ω^{2} \frac{m}{k_{e}}$

La diagonal de la matriz D contiene los valores propios λ.

>> K=sym([2,-1,0,-1;-1,2,-1,0;0,-1,2,-1;-1,0,-1,2]);
>> [V,D]=eig(K)
V =
[1, -1, -1,  0]
[1,  1,  0, -1]
[1, -1,  1,  0]
[1,  1,  0,  1]
 
D =
[0, 0, 0, 0]
[0, 4, 0, 0]
[0, 0, 2, 0]
[0, 0, 0, 2]

$D = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 2 \end{matrix}), {\begin{cases} ω_{1}^{2} = 0 \\ ω_{2}^{2} = 4 \frac{k_{e}}{m} \\ ω_{3}^{2} = 2 \frac{k_{e}}{m} \\ ω_{4}^{2} = 2 \frac{k_{e}}{m} \end{cases}$

Vectores propios

Los vectores propios correspondientes a cada valor propio son las columnas de la matriz V

$\begin{array}{l} V = (\begin{matrix} 1 & - 1 & - 1 & 0 \\ 1 & 1 & 0 & - 1 \\ 1 & - 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \end{matrix}) \\ X^{(1)} = (\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}), X^{(2)} = (\begin{matrix} - 1 \\ 1 \\ - 1 \\ 1 \end{matrix}), X^{(3)} = (\begin{matrix} 1 \\ 0 \\ 1 \\ 0 \end{matrix}), X^{(4)} = (\begin{matrix} 0 \\ - 1 \\ 0 \\ 1 \end{matrix}) \end{array}$

Vamos a dividir los vectores X⁽¹⁾, X⁽²⁾, X⁽³⁾ y X⁽⁴⁾ por un factor de escala de modo que

${(X^{(i)})}^{T} M X^{(i)} = 1$

>> M=diag([1,1,1,1]);
>> X1=V(:,1);
>> r=X1'*M*X1
r =4
>> X2=V(:,2);
>> r=X2'*M*X2
r =4
>> X3=V(:,3);
>> r=X3'*M*X3
r =2
>> X4=V(:,4);
>> r=X4'*M*X4
r =2
>> X1=X1/2;
>> X2=X2/2;
>> X3=X3/sym(sqrt(2));
>> X4=X4/sym(sqrt(2));

El vector X⁽¹⁾, se divide entre dos, el vector X⁽²⁾, se divide entre dos, X⁽³⁾ entre $\sqrt{2}$ y X⁽⁴⁾ entre $\sqrt{2}$

$X^{(1)} = \frac{1}{2} (\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}), X^{(2)} = \frac{1}{2} (\begin{matrix} - 1 \\ 1 \\ - 1 \\ 1 \end{matrix}), X^{(3)} = \frac{\sqrt{2}}{2} (\begin{matrix} - 1 \\ 0 \\ 1 \\ 0 \end{matrix}), X^{(4)} = \frac{\sqrt{2}}{2} (\begin{matrix} 0 \\ - 1 \\ 0 \\ 1 \end{matrix})$

La nueva matriz V, formada por los vectores columna es

$V = \frac{1}{2} (\begin{matrix} 1 & - 1 & - \sqrt{2} & 0 \\ 1 & 1 & 0 & - \sqrt{2} \\ 1 & - 1 & \sqrt{2} & 0 \\ 1 & 1 & 0 & \sqrt{2} \end{matrix})$

>> V=[X1,X2,X3,X4]
V =
[1/2, -1/2, -2^(1/2)/2,          0]
[1/2,  1/2,          0, -2^(1/2)/2]
[1/2, -1/2,  2^(1/2)/2,          0]
[1/2,  1/2,          0,  2^(1/2)/2]

Superposición

Ecuaciones del movimiento desacopladas

${\begin{cases} \frac{d^{2} u_{1}}{d t^{2}} + ω_{1}^{2} u_{1} = 0 \\ \frac{d^{2} u_{2}}{d t^{2}} + ω_{2}^{2} u_{2} = 0 \\ \frac{d^{2} u_{3}}{d t^{2}} + ω_{3}^{2} u_{3} = 0 \\ \frac{d^{2} u_{4}}{d t^{2}} + ω_{4}^{2} u_{4} = 0 \end{cases}$

Las nuevas ecuaciones del movimiento expresadas en términos de las coordenadas u(t) están desacopladas y sus soluciones son conocidas: movimiento rectilíneo uniforme para ω₁=0, y Movimiento Armónico Simple para ω₂ y ω₃. Las soluciones de estas ecuaciones diferenciales son:

$\begin{array}{l} {\begin{cases} u_{1} (t) = B_{1} t + A_{1} \\ u_{2} (t) = A_{2} \cos (ω_{2} t) + B_{2} \sin (ω_{2} t) \\ u_{3} (t) = A_{3} \cos (ω_{3} t) + B_{3} \sin (ω_{3} t) \\ u_{4} (t) = A_{4} \cos (ω_{4} t) + B_{4} \sin (ω_{4} t) \end{cases} \\ {\begin{cases} \frac{d u_{1}}{d t} = B_{1} \\ \frac{d u_{2}}{d t} = - ω_{2} A_{2} \sin (ω_{2} t) + ω_{2} B_{2} \cos (ω_{2} t) \\ \frac{d u_{3}}{d t} = - ω_{3} A_{3} \sin (ω_{3} t) + ω_{3} B_{3} \cos (ω_{3} t) \\ \frac{d u_{4}}{d t} = - ω_{4} A_{4} \sin (ω_{4} t) + ω_{4} B_{4} \cos (ω_{4} t) \end{cases} \end{array}$

donde las constantes A_i y B_i se determinan a partir de las condiciones iniciales

$u (0) {\begin{cases} u_{1} (0) = A_{1} \\ u_{2} (0) = A_{2} \\ u_{3} (0) = A_{3} \\ u_{4} (0) = A_{4} \end{cases}, {\frac{d u}{d t} |}_{t = 0} {\begin{cases} {\frac{d u_{1}}{d t} |}_{0} = B_{1} \\ {\frac{d u_{2}}{d t} |}_{0} = ω_{2} B_{2} \\ {\frac{d u_{3}}{d t} |}_{0} = ω_{3} B_{3} \\ {\frac{d u_{4}}{d t} |}_{0} = ω_{4} B_{4} \end{cases}$

Condiciones iniciales

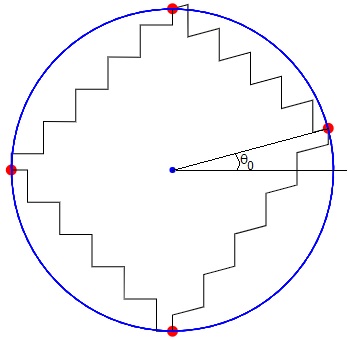
Las condiciones inicales vienen determinadas por el desplazamiento y velocidad de cada una de las partículas en el instante t=0. Todas las partículas parten de su posición inicial en equilibrio en reposo, salvo la primera partícula a la que se le proporciona un desplazamiento θ₀.

Las condiciones iniciales en el espacio u se escriben en forma matricial

$\begin{array}{l} u (0) = V^{- 1} θ (0) \\ {\frac{d u}{d t} |}_{t = 0} = V^{- 1} {\frac{d θ}{d t} |}_{t = 0} \end{array}$

Las partículas parten del reposo, entonces A₁=0, B₂=0, B₃=0 y B₄=0

Se desplaza la primera partícula de la posición de equlibrio

>> x0=[1;0;0;0];
>> u0=V^-1*x0
u0 =
       1/2
      -1/2
-2^(1/2)/2
         0

${\begin{cases} A_{1} = \frac{1}{2} θ_{0} \\ A_{2} = - \frac{1}{2} θ_{0} \\ A_{3} = - \frac{\sqrt{2}}{2} θ_{0} \\ A_{4} = 0 \end{cases}$

Las ecuaciones del movimiento en el espacio u(t) son

${\begin{cases} u_{1} (t) = \frac{θ_{0}}{2} \\ u_{2} (t) = - \frac{θ_{0}}{2} \cos (ω_{2} t) \\ u_{3} (t) = - \frac{\sqrt{2}}{2} θ_{0} \cos (ω_{3} t) \\ u_{4} (t) = 0 \end{cases}$

Finalmente, el desplazamiento de cada una de las partículas respecto del tiempo, el vector x se obtiene, multiplicando la matriz V por el vector u

$\begin{array}{l} θ (t) = V \cdot u (t) \\ (\begin{matrix} θ_{1} (t) \\ θ_{2} (t) \\ θ_{3} (t) \\ θ_{4} (t) \end{matrix}) = \frac{1}{2} (\begin{matrix} 1 & - 1 & - \sqrt{2} & 0 \\ 1 & 1 & 0 & - \sqrt{2} \\ 1 & - 1 & \sqrt{2} & 0 \\ 1 & 1 & 0 & \sqrt{2} \end{matrix}) (\begin{matrix} u_{1} (t) \\ u_{2} (t) \\ u_{3} (t) \\ u_{4} (t) \end{matrix}) \end{array}$

El resultado final es

${\begin{cases} θ_{1} (t) = \frac{θ_{0}}{2} (\frac{1}{2} + \frac{1}{2} \cos (ω_{2} t) + \cos (ω_{3} t)) \\ θ_{2} (t) = \frac{θ_{0}}{2} (\frac{1}{2} - \frac{1}{2} \cos (ω_{2} t)) \\ θ_{3} (t) = \frac{θ_{0}}{2} (\frac{1}{2} + \frac{1}{2} \cos (ω_{2} t) - \cos (ω_{3} t)) \\ θ_{4} (t) = \frac{θ_{0}}{2} (\frac{1}{2} - \frac{1}{2} \cos (ω_{2} t)) \end{cases}$

Coinciden θ₂(t) y θ₄(t)

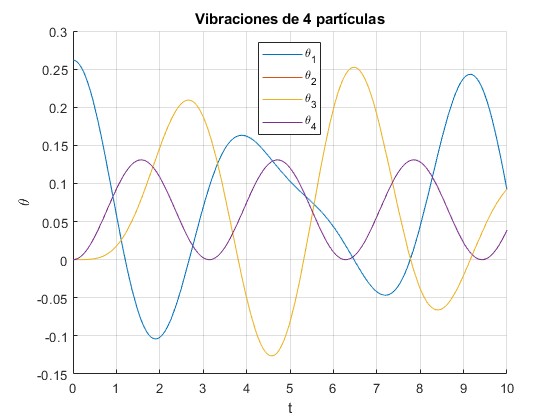
Representamos el desplazamiento de cada una de las tres partículas θ₁(t), θ₂(t), θ₃(t) y θ₃(t) para el siguiente sistema:

Constante efectiva muelles, k_e=1. Masa de las partículas m=1
Desplazamiento de la primera partícula, θ₀=π/12 (15°)

w2=2; %frecuencias de los modos normales de vibración
w3=sqrt(2);
th_0=pi/12; % 15º desplazamiento

x1=@(t) th_0*(1/2+cos(w2*t)/2+cos(w3*t))/2;
x2=@(t) th_0*(1/2-cos(w2*t)/2)/2;
x3=@(t) th_0*(1/2+cos(w2*t)/2-cos(w3*t))/2;
x4=@(t) th_0*(1/2-cos(w2*t)/2)/2;
hold on
fplot(x1,[0,10])
fplot(x2,[0,10])
fplot(x3,[0,10])
fplot(x4,[0,10])
hold off
xlabel('t')
legend('\theta_1', '\theta_2', '\theta_3', '\theta_4', 'location', 'best')
ylabel('\theta')
grid on
title('Vibraciones de 4 partículas')

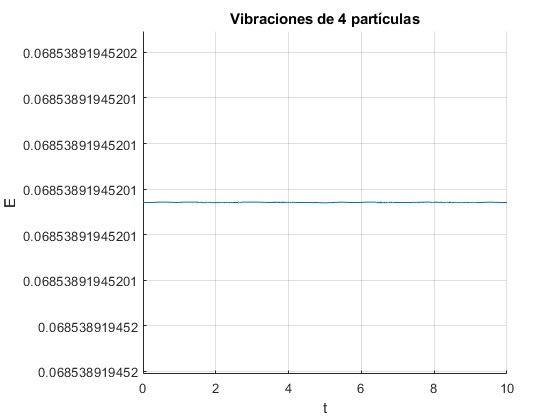
Comprobamos que la energía E se mantiene constante

$E = \frac{1}{2} m R^{2} {{(\frac{d θ_{1}}{d t})}^{2} + {(\frac{d θ_{2}}{d t})}^{2} + {(\frac{d θ_{3}}{d t})}^{2} + {(\frac{d θ_{4}}{d t})}^{2}} + \frac{1}{2} k_{e} R^{2} {{(θ_{2} - θ_{1})}^{2} + {(θ_{3} - θ_{2})}^{2} + {(θ_{4} - θ_{3})}^{2} + {(θ_{1} - θ_{4})}^{2}}$

w2=2; %frecuencias de los modos normales de vibración
w3=sqrt(2);
th_0=pi/12; % 15º desplazamiento
x1=@(t) th_0*(1/2+cos(w2*t)/2+cos(w3*t))/2;
x2=@(t) th_0*(1/2-cos(w2*t)/2)/2;
x3=@(t) th_0*(1/2+cos(w2*t)/2-cos(w3*t))/2;
x4=@(t) th_0*(1/2-cos(w2*t)/2)/2;

v1=@(t) th_0*(-w2*sin(w2*t)/2-w3*sin(w3*t))/2;
v2=@(t) th_0*(w2*sin(w2*t)/2)/2;
v3=@(t) th_0*(-w2*sin(w2*t)/2+w3*sin(w3*t))/2;
v4=@(t) th_0*(w2*sin(w2*t)/2)/2;

E=@(t) (v1(t).^2+v2(t).^2+v3(t).^2+v4(t).^2)/2+((x2(t)-x1(t)).^2+
(x3(t)-x2(t)).^2+(x4(t)-x3(t)).^2+(x1(t)-x4(t)).^2)/2;
hold on
fplot(E,[0,10])
hold off
xlabel('t')
ylabel('E')
grid on
title('Vibraciones de 4 partículas')

Actividades

Desplazamos la primera partícula un ángulo θ₀ y la soltamos. Observamos las vibraciones del sistema de cuatro partículas

Sistema de n=6 partículas

Consideremos un sistema de n=6 partículas de la misma masa m, conectadas por muelles elásticos de la misma constante k y obligadas a moverse por una pista circular de radio R

La deducción es similar al caso n=4, por lo que solamente daremos los resultados

La matriz K es

$K = (\begin{matrix} 2 & - 1 & 0 & 0 & 0 & - 1 \\ - 1 & 2 & - 1 & 0 & 0 & 0 \\ 0 & - 1 & 2 & - 1 & 0 & 0 \\ 0 & 0 & - 1 & 2 & - 1 & 0 \\ 0 & 0 & 0 & - 1 & 2 & - 1 \\ - 1 & 0 & 0 & 0 & - 1 & 2 \end{matrix})$

Calculamos los valores propios, proporcinales a los cuadrados de las frecuencias ω² de vibración

K=sym(diag(2*ones(1,6))+diag(-ones(1,5),1)+diag(-ones(1,5),-1));
K(1,6)=sym(-1);
K(6,1)=sym(-1);

D =
[0, 0, 0, 0, 0, 0]
[0, 4, 0, 0, 0, 0]
[0, 0, 1, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 3, 0]
[0, 0, 0, 0, 0, 3]

$ω_{1}^{2} = 0, ω_{2}^{2} = 4 \frac{k_{e}}{m}, ω_{3}^{2} = \frac{k_{e}}{m}, ω_{4}^{2} = \frac{k_{e}}{m}, ω_{5}^{2} = 3 \frac{k_{e}}{m}, ω_{6}^{2} = 3 \frac{k_{e}}{m}$

Vectores propios

Los vectores propios correspondientes a cada valor propio son las columnas de la matriz V

V =
[1, -1, -1,  1, -1, -1]
[1,  1, -1,  0,  1,  0]
[1, -1,  0, -1,  0,  1]
[1,  1,  1, -1, -1, -1]
[1, -1,  1,  0,  1,  0]
[1,  1,  0,  1,  0,  1]

Vamos a dividir los vectores X⁽¹⁾, X⁽²⁾, X⁽³⁾, X⁽⁴⁾, X⁽⁵⁾ y X⁽⁶⁾ por un factor de escala de modo que

${(X^{(i)})}^{T} M X^{(i)} = 1$

 K=sym(diag(2*ones(1,6))+diag(-ones(1,5),1)+diag(-ones(1,5),-1));
 K(1,6)=sym(-1);
 K(6,1)=sym(-1);
 V,D]=eig(K);
 M=diag(ones(1,6));
 X1=V(:,1);
 X2=V(:,2);
 X3=V(:,3);
 X4=V(:,4);
 X5=V(:,5);
 X6=V(:,6);
 r=X1'*M*X1;
 X1=X1/sym(sqrt(r));
 r=X2'*M*X2;
 X2=X2/sym(sqrt(r));
 r=X3'*M*X3;
 X3=X3/sym(sqrt(r));
 r=X4'*M*X4;
 X4=X4/sym(sqrt(r));
 r=X5'*M*X5;
 X5=X5/sym(sqrt(r));
 r=X6'*M*X6;
 X6=X6/sym(sqrt(r));
 V=[X1,X2,X3,X4,X5,X6];

La nueva matriz V, formada por los vectores columna es

V =
[6^(1/2)/6, -6^(1/2)/6, -1/2,  1/2, -1/2, -1/2]
[6^(1/2)/6,  6^(1/2)/6, -1/2,    0,  1/2,    0]
[6^(1/2)/6, -6^(1/2)/6,    0, -1/2,    0,  1/2]
[6^(1/2)/6,  6^(1/2)/6,  1/2, -1/2, -1/2, -1/2]
[6^(1/2)/6, -6^(1/2)/6,  1/2,    0,  1/2,    0]
[6^(1/2)/6,  6^(1/2)/6,    0,  1/2,    0,  1/2]

$V = (\begin{matrix} \frac{\sqrt{6}}{6} & - \frac{\sqrt{6}}{6} & - \frac{1}{2} & \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} \\ \frac{\sqrt{6}}{6} & \frac{\sqrt{6}}{6} & - \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ \frac{\sqrt{6}}{6} & - \frac{\sqrt{6}}{6} & 0 & - \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{\sqrt{6}}{6} & \frac{\sqrt{6}}{6} & \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} \\ \frac{\sqrt{6}}{6} & - \frac{\sqrt{6}}{6} & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ \frac{\sqrt{6}}{6} & \frac{\sqrt{6}}{6} & 0 & \frac{1}{2} & 0 & \frac{1}{2} \end{matrix})$

Condiciones iniciales

Las condiciones iniciales en el espacio u se escriben en forma matricial

$\begin{array}{l} u (0) = V^{- 1} θ (0) \\ {\frac{d u}{d t} |}_{t = 0} = V^{- 1} {\frac{d θ}{d t} |}_{t = 0} \end{array}$

Las partículas parten del reposo, entonces B₁=0, B₂=0, B₃=0, B₄=0, B₅=0 y B₆=0

Se desplaza la primera partícula de la posición de equlibrio

>> x0=[1;0;0;0;0;0];
>> u0=V^-1*x0 % V^-1 matriz inversa de V
u0 =
 6^(1/2)/6
-6^(1/2)/6
      -1/3
       1/3
      -1/3
      -1/3

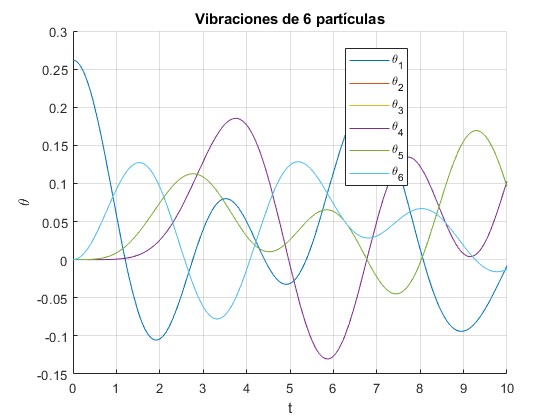
$\begin{array}{l} A_{1} = \frac{\sqrt{6}}{6}, A_{2} = - \frac{\sqrt{6}}{6}, A_{3} = - \frac{1}{2}, A_{4} = \frac{1}{2}, A_{5} = - \frac{1}{2}, A_{6} = - \frac{1}{2} \\ {\begin{cases} u_{1} (t) = \frac{\sqrt{6}}{6} θ_{0} \\ u_{2} (t) = - \frac{\sqrt{6}}{6} θ_{0} \cos (ω_{2} t) \\ u_{3} (t) = - \frac{1}{3} θ_{0} \cos (ω_{3} t) \\ u_{4} (t) = \frac{1}{3} θ_{0} \cos (ω_{4} t) \\ u_{5} (t) = - \frac{1}{3} θ_{0} \cos (ω_{5} t) \\ u_{6} (t) = - \frac{1}{3} θ_{0} \cos (ω_{6} t) \end{cases} \end{array}$

Los desplazamientos de las partículas θ_i(t), i=1,2,...6 son

$\begin{array}{l} θ (t) = V \cdot u (t) \\ {\begin{cases} θ_{1} (t) = \frac{θ_{0}}{6} (1 + \cos (ω_{2} t) + \cos (ω_{3} t) + \cos (ω_{4} t) + \cos (ω_{5} t) + \cos (ω_{6} t)) \\ θ_{2} (t) = \frac{θ_{0}}{6} (1 - \cos (ω_{2} t) + \cos (ω_{3} t) - \cos (ω_{5} t)) \\ θ_{3} (t) = \frac{θ_{0}}{6} (1 + \cos (ω_{2} t) - \cos (ω_{4} t) - \cos (ω_{6} t)) \\ θ_{4} (t) = \frac{θ_{0}}{6} (1 - \cos (ω_{2} t) - \cos (ω_{3} t) - \cos (ω_{4} t) + \cos (ω_{5} t) + \cos (ω_{6} t)) \\ θ_{5} (t) = \frac{θ_{0}}{6} (1 + \cos (ω_{2} t) - \cos (ω_{3} t) - \cos (ω_{5} t)) \\ θ_{6} (t) = \frac{θ_{0}}{6} (1 - \cos (ω_{2} t) + \cos (ω_{4} t) - \cos (ω_{6} t)) \end{cases} \end{array}$

w2=2; %frecuencias de los modos normales de vibración
w3=1;
w4=1; 
w5=sqrt(3);
w6=sqrt(3);
th_0=pi/12; % 15º desplazamiento
x1=@(t) th_0*(1+cos(w2*t)+cos(w3*t)+cos(w4*t)+cos(w5*t)+cos(w6*t))/6;
x2=@(t) th_0*(1-cos(w2*t)+cos(w3*t)-cos(w5*t))/6;
x3=@(t) th_0*(1+cos(w2*t)-cos(w4*t)-cos(w6*t))/6;
x4=@(t) th_0*(1-cos(w2*t)-cos(w3*t)-cos(w4*t)+cos(w5*t)+cos(w6*t))/6;
x5=@(t) th_0*(1+cos(w2*t)-cos(w3*t)-cos(w5*t))/6;
x6=@(t) th_0*(1-cos(w2*t)+cos(w4*t)-cos(w6*t))/6;

hold on
fplot(x1,[0,10])
fplot(x2,[0,10])
fplot(x3,[0,10])
fplot(x4,[0,10])
fplot(x5,[0,10])
fplot(x6,[0,10])
hold off
xlabel('t')
legend('\theta_1', '\theta_2', '\theta_3', '\theta_4', '\theta_5', '\theta_6',
'location', 'best')
ylabel('\theta')
grid on
title('Vibraciones de 6 partículas')

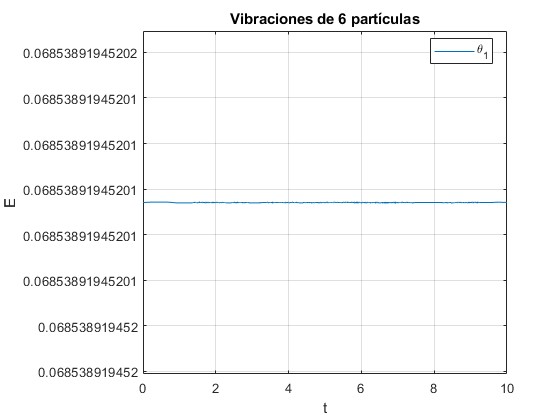
Comprobamos que la energía E se mantiene constante

w2=2; %frecuencias de los modos normales de vibración
w3=1;
w4=1; 
w5=sqrt(3);
w6=sqrt(3);
th_0=pi/12; % 15º desplazamiento
x1=@(t) th_0*(1+cos(w2*t)+cos(w3*t)+cos(w4*t)+cos(w5*t)+cos(w6*t))/6;
x2=@(t) th_0*(1-cos(w2*t)+cos(w3*t)-cos(w5*t))/6;
x3=@(t) th_0*(1+cos(w2*t)-cos(w4*t)-cos(w6*t))/6;
x4=@(t) th_0*(1-cos(w2*t)-cos(w3*t)-cos(w4*t)+cos(w5*t)+cos(w6*t))/6;
x5=@(t) th_0*(1+cos(w2*t)-cos(w3*t)-cos(w5*t))/6;
x6=@(t) th_0*(1-cos(w2*t)+cos(w4*t)-cos(w6*t))/6;

v1=@(t) th_0*(-w2*sin(w2*t)-w3*sin(w3*t)-w4*sin(w4*t)-w5*sin(w5*t)-w6*sin(w6*t))/6;
v2=@(t) th_0*(w2*sin(w2*t)-w3*sin(w3*t)+w5*sin(w5*t))/6;
v3=@(t) th_0*(-w2*sin(w2*t)+w4*sin(w4*t)+w6*sin(w6*t))/6;
v4=@(t) th_0*(w2*sin(w2*t)+w3*sin(w3*t)+w4*sin(w4*t)-w5*sin(w5*t)-w6*sin(w6*t))/6;
v5=@(t) th_0*(-w2*sin(w2*t)+w3*sin(w3*t)+w5*sin(w5*t))/6;
v6=@(t) th_0*(w2*sin(w2*t)-w4*sin(w4*t)+w6*sin(w6*t))/6;


E=@(t) (v1(t).^2+v2(t).^2+v3(t).^2+v4(t).^2+v5(t).^2+v6(t).^2)/2+
((x2(t)-x1(t)).^2+(x3(t)-x2(t)).^2+(x4(t)-x3(t)).^2+(x5(t)-x4(t)).^2+
(x6(t)-x5(t)).^2+(x1(t)-x6(t)).^2)/2;
fplot(E,[0,10])
xlabel('t')
ylabel('E')
grid on
title('Vibraciones de 6 partículas')

Actividades

Desplazamos la primera partícula partícula un ángulo θ₀ y la soltamos. Observamos las vibraciones del sistema de seis partículas

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1125, pp. 211-213