Estática

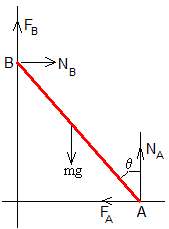
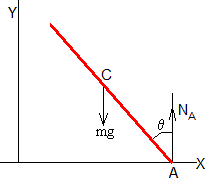
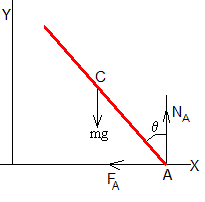
Supongamos una escalera homogénea de masa m y longitud l apoyada en dos paredes perpendiculares en los puntos A (lsinθ,0) y B (0, lcosθ,0), siendo θ el ángulo que forma la escalera con el eje vertical Y. Las fuerzas sobre la escalera son las que se ha dibujado en la figura.

• F_A y F_B son las fuerzas de rozamiento que ejercen las paredes vertical y horizontal en los respectivos apoyos.

• N_A y N_B son las reacciones de la pared en los puntos de apoyo

• mg es el peso que actúa en el centro de masas de la escalera a una distancia d de A. Si la escalera es homogénea d=l/2.

La situación de equilibrio solamente nos proporciona tres ecuaciones (dos para las fuerzas y una para los momentos), sin embargo, tenemos cuatro incógnitas, el problema es indeterminado.

${\displaystyle \begin{array}{l}\{\begin{array}{l}{F}_A=N_B\\ N_A+F_B=mg\end{array}\hfill \\ -F_{B}l\sin \theta -N_{B}l\cos \theta +mg\frac{l}{2}\sin \theta =0\hfill \end{array}}$

Para que la escalera pernanezca en equilibrio se tiene que cumplir que las fuerzas de rozamiento F_A y F_B sean menores que sus valores máximos. Si μ_A y μ_B son los coeficientes estáticos en las paredes vertical y horizontal, respectivamente

${\displaystyle \{\begin{array}{l}{F}_A\le {\mu }_A{N}_A\\ F_B\le {\mu }_B{N}_B\end{array}}$

Estas dos desigualdades conducen a una relación entre ambos coeficientes de rozamiento. De la tercera ecuación de equilibrio, la de los momentos, despejamos F_B

${\displaystyle F_B=\frac{1}{2}mg-\frac{N_B}{\tan \theta }}$

A partir de ambas desigualdades obtenemos

${\displaystyle \begin{array}{l}{F}_B\le {\mu }_B{N}_B{N}_B\ge \frac{1/2}{{\mu }_B+1/\tan \theta }mg\\ F_A\le {\mu }_A{N}_A{N}_B\le {\mu }_A(mg-F_B)N_B\le \frac{{\mu }_A/2}{1-{\mu }_A/\tan \theta }mg\\ \frac{1/2}{{\mu }_B+1/\tan \theta }mg\le \frac{{\mu }_A/2}{1-{\mu }_A/\tan \theta }mg\\ \tan \theta \le \frac{2{\mu }_A}{1-{\mu }_A{\mu }_B}\end{array}}$

Esta es la relación entre los parámetros de la escalera. Si se incrementa el ángulo θ, se alcanza un ángulo θ_s en el que la escalera empieza a deslizar. Para este ángulo al menos una de las dos desigualdades deja de cumplirse, F_A>μ_A·N_A y/o F_B>μ_B·N_B. El caso más sencillo se produce cuando F_B=0, no hay rozamiento en la pared vertical, entonces tanθ≤2μ_A. El ángulo límite es tanθ_s=2μ_A

• La escalera está en equilibrio, en reposo, cuando el ángulo θ que forma con la vertical es θ<θ_s

• La escalera empieza a deslizar cuando el ángulo θ que forma con la dirección vertical es θ≥θ_s.

Paredes lisas (sin rozamiento)

El caso más sencillo corresponde a una escalera apoyada en paredes perpendiculares sin rozamiento. Cualquiera que sea el ángulo 0<θ<π/2, la escalera empieza a deslizar

El extremo B de la escalera permanece en contacto con la pared vertical

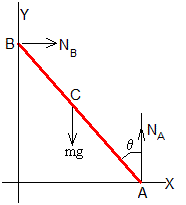
Supondremos que la escalera es un sólido rígido en forma de varilla, de masa m y longitud l. Su momento de inercia respecto a un eje perpendicular al plano de la escalera y que pasa por el centro de masas es I_c=ml²/12

La dinámica de la escalera se describe mediante dos ecuaciones:

• La ecuación del movimiento de traslación del centro de masas
• La ecuación de la dinámica de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas C

La posición, velocidad y aceleración del centro de masas C son:

${\displaystyle \begin{array}{l}{\overrightarrow{r}}_c=\frac{l}{2}\left(\sin \theta \widehat{i}+\cos \theta \widehat{j}\right)\\ {\overrightarrow{v}}_c=\frac{d{\overrightarrow{r}}_c}{dt}=\frac{l}{2}\left(\cos \theta \widehat{i}-\sin \theta \widehat{j}\right)\frac{d\theta }{dt}\\ {\overrightarrow{a}}_c=\frac{d{\overrightarrow{v}}_c}{dt}=\frac{l}{2}\left(\cos \theta \widehat{i}-\sin \theta \widehat{j}\right)\frac{d^2\theta }{dt}-\frac{l}{2}\left(\sin \theta \widehat{i}+\cos \theta \widehat{j}\right){\left(\frac{d\theta }{dt}\right)}^2=\\ \frac{l}{2}\left(\cos \theta \frac{d^2\theta }{dt}-\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{i}-\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{dt}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{j}\end{array}}$

La ecuación del movimiento de traslación del centro de masas es

${\displaystyle m{\overrightarrow{a}}_c=N_B\widehat{i}+\left(N_A-mg\right)\widehat{j}\{\begin{array}{l}{N}_B=m\frac{l}{2}\left(\cos \theta \frac{d^2\theta }{d{t}^2}-\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\\ N_A-mg=-m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{d{t}^2}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\end{array}}$

La ecuación de la dinámica de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas C es

${\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=N_A\frac{l}{2}\sin \theta -N_B\frac{l}{2}\cos \theta \\ \frac{1}{12}m{l}^2\frac{d^2\theta }{d{t}^2}=\frac{l}{2}\left\{\begin{array}{l}mg\sin \theta -m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{dt}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\sin \theta -\\ m\frac{l}{2}\left(\cos \theta \frac{d^2\theta }{dt}-\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\cos \theta \end{array}\right\}\\ \frac{d^2\theta }{d{t}^2}=\frac{3}{2}\frac{g}{l}\sin \theta \end{array}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0. Se suelta la escalera cuando forma un ángulo θ₀ con la dirección vertical

El ángulo θ va creciendo a medida que la escalera va cayendo, hasta que la reacción N_B se hace cero.

${\displaystyle N_B=m\frac{l}{2}\left(\cos \theta \frac{3}{2}\frac{g}{l}\sin \theta -\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\right)=m\frac{l}{2}\sin \theta \left(\frac{3}{2}\frac{g}{l}\cos \theta -{\left(\frac{d\theta }{dt}\right)}^2\right)}$

Resolvemos la ecuación diferencial del movimiento, utilizando la función ode45 de MATLAB, partiendo del ángulo θ₀=π/6 (30°). Detenemos el proceso de integración cuando el ángulo θ=π/2, la escalera impacta con el suelo. Para ello definimos la función stop_escalera_1

function [value,isterminal,direction]=stop_escalera_1(t,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

Representamos la reacción N_B en función del ángulo θ, señalamos la raíz θ_l, cuando N_B=0, que calcularemos más adelante empleando el principio de conservación de la energía. En esa posición la escalera deja de tener contacto con la pared vertical por lo que tendremos que plantear otras ecuaciones para describir el movimiento de la escalera desde dicha posición θ_l hasta que impacta con el suelo θ=π/2

L=1; %longitud de la escalera
th_0=pi/6; %ángulo inicial

f=@(t,x) [x(2);3*9.8*sin(x(1))/(2*L)]; 
opts=odeset('events',@stop_escalera_1);
[t,x]=ode45(f,[0,1],[th_0,0],opts);
N_B=L*sin(x(:,1)).*(3*9.8*cos(x(:,1))/(2*L)-x(:,2).^2)/2;
hold on
plot(x(:,1), N_B);
th_L=acos(2*cos(th_0)/3);
plot(th_L,0, 'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
ylabel('N_B')
xlabel('\theta')
title('Escalera, sin rozamiento')

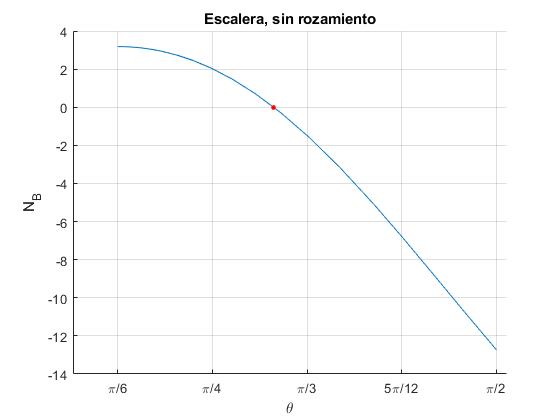
El ángulo límite θ_l=0.95 (55°)

>> th_L*180/pi
ans =   54.7356

Conservación de la energía

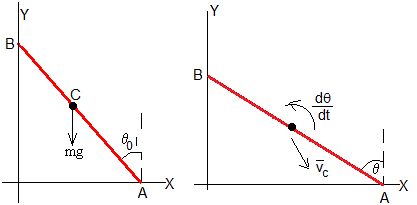
Aplicamos el principio de conservación de la energía para determinar dicho ángulo. En las figuras, comparamos la situación inicial y en el instante t. La energía potencial del c.m. se va convirtiendo en energía cinética de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m.

${\displaystyle \begin{array}{l}mg\frac{l}{2}\cos {\theta }_0=\frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2+mg\frac{l}{2}\cos \theta \\ mg\frac{l}{2}\cos {\theta }_0-mg\frac{l}{2}\cos \theta =\frac{1}{2}m\frac{l^2}{4}\left({\cos }^2\theta +{\sin }^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}\frac{1}{12}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2\\ {\left(\frac{d\theta }{dt}\right)}^2=3\frac{g}{l}\left(\cos {\theta }_0-\cos \theta \right)\end{array}}$

Las reacciones en A y en B valen

${\displaystyle \{\begin{array}{l}{N}_B=3mg\sin \theta \left(\frac{3}{2}\cos \theta -\cos {\theta }_0\right)\\ N_A=mg-m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{dt}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)=\frac{5}{2}mg\left(\frac{3}{2}{\sin }^2\theta -\cos \theta \cos {\theta }_0\right)\end{array}}$

N_B se hace cero para el ángulo

${\displaystyle {\theta }_l=\arccos \left(\frac{2}{3}\cos {\theta }_0\right)}$

En esta posición, la velocidad angular de rotación alrededor de un eje que pasa por el c.m. es

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_l^2=3\frac{g}{l}\left(\cos {\theta }_0-\cos {\theta }_l\right)=\frac{g}{l}\cos {\theta }_0}$

El extremo B de la escalera deja de estar en contacto con la pared vertical

La dinámica de la escalera se describe mediante dos ecuaciones:

• La ecuación del movimiento de traslación del centro de masas
• La ecuación de la dinámica de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas C

A partir de la posición θ_l, las ecuaciones del movimiento de la escalera son:

Ecuación del movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}m{\overrightarrow{a}}_c=\left(N_A-mg\right)\widehat{j}\\ \{m\left(\frac{d^{2}x}{d{t}^2}\widehat{i}+\frac{d^{2}y}{d{t}^2}\widehat{j}\right)=\left(N_A-mg\right)\widehat{j}\{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=0\\ m\left\{-\frac{l}{2}\sin \theta \frac{d^2\theta }{d{t}^2}-\frac{l}{2}\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right\}=N_A-mg\end{array}\end{array}}$

Ecuación de la dinámica de rotación alrededor de de un eje perpendicular al plano de la escalera que pasa por el centro de masas C

${\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=N_A\frac{l}{2}\sin \theta \\ \frac{1}{12}m{l}^2\frac{d^2\theta }{d{t}^2}=\frac{l}{2}\left\{mg-m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{dt}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\right\}\sin \theta \\ \left(\frac{1}{3}+{\sin }^2\theta \right)\frac{d^2\theta }{d{t}^2}=\left(2\frac{g}{l}-\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\sin \theta \end{array}}$

La velocidad horizontal del centro de masas dx/dt es constante, ya que no hay ninguna fuerza horizontal. Esta es la velocidad del c.m. en la posición θ_l

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{l}{2}\cos \theta \frac{d\theta }{dt}\\ {\frac{dx}{dt}|}_{\theta ={\theta }_l}=\frac{l}{3}\cos {\theta }_0\sqrt{\frac{g}{l}\cos {\theta }_0}=\frac{1}{3}\sqrt{gl}{\cos }^{3/2}{\theta }_0\end{array}}$

Se resuelve la ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{\left(2\frac{g}{l}-\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\sin \theta }{\frac{1}{3}+{\sin }^2\theta }}$

mediante la función ode45 de MATLAB, con las siguientes condiciones iniciales, en el instante t=t_l, la posición de la escalera es θ=θ_l y su velocidad angular inicial es

${\displaystyle {\frac{d\theta }{dt}|}_l=\sqrt{\frac{g}{l}\cos {\theta }_0}}$

Movimiento completo

El movimiento de la escalera desde la posición inicial θ₀ hasta la posición final π/2, se describe mediante dos ecuaciones diferenciales de segundo orden:

• la primera, en el intervalo (θ₀, θ_l)

${\displaystyle \frac{d^2\theta }{d{t}^2}=f\left(\theta ,\frac{d\theta }{dt}\right)}$

• la segunda, en el intervalo (θ_l, π/2)

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=v_{xl}\\ \frac{d^2\theta }{d{t}^2}=g\left(\theta ,\frac{d\theta }{dt}\right)\end{array}}$

Definimos dos funciones: una función que detenga el primer proceso de integración cuando se alcance el ángulo θ_l. Otra función, para el segundo proceso de integración que comienza en éste ángulo y se detiene para el ángulo π/2

function [value,isterminal,direction]=stop_escalera(t,x, th_L)
    value=x(1)-th_L;  
    isterminal=1;
    direction=1; 
end

function [value,isterminal,direction]=stop_escalera_1(t,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

Consideremos una escalera de longitud l=1, que se suelta cuando forma un ángulo θ₀=π/6 (30°) con la vertical. Representamos el ángulo θ que hace la escalera con la dirección vertical en función del tiempo t

L=1; %longitud de la escalera
th_0=pi/6; %ángulo inicial
th_L=acos(2*cos(th_0)/3); %ángulo límite para reacción nula

f=@(t,x) [x(2);3*9.8*sin(x(1))/(2*L)]; 
opts=odeset('events',@(t,x) stop_escalera(t,x, th_L));
[t,x]=ode45(f,[0,10],[th_0,0],opts);
hold on
plot(t,x(:,1));
tL=t(end); %final del primer proceso

opts=odeset('events',@stop_escalera_1);
f=@(t,x) [x(2);(2*9.8/L-cos(x(1))*x(2)^2)*sin(x(1))/(1/3+sin(x(1))^2)]; 
[t,x]=ode45(f,[0,10],[th_L,sqrt(9.8*cos(th_0)/L)],opts);
plot(t+tL,x(:,1))

line([0,tL],[th_L,th_L],'lineStyle','--')
line([tL,tL],[0,th_L],'lineStyle','--')
hold off
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('t')
ylabel('\theta')
title('Escalera, sin rozamiento')

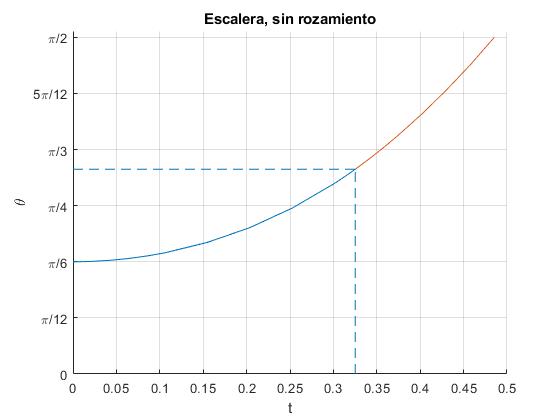
La velocidad angular final de la escalera es

>> x(end,2)
ans =    4.8300

Conservación de la energía

Calculamos esta velocidad angular final aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}mg\frac{l}{2}\cos {\theta }_0=\frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2+mg\frac{l}{2}\cos \theta \\ mg\frac{l}{2}\cos {\theta }_0=\frac{1}{2}m\left\{{\left(\frac{dx}{dt}\right)}^2+{\left(-\frac{l}{2}\sin \theta \frac{d\theta }{dt}\right)}^2\right\}+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2+mg\frac{l}{2}\cos \theta \\ g\cos {\theta }_0=\frac{1}{9}g{\cos }^3{\theta }_0+\frac{l}{4}\left({\sin }^2\theta +\frac{1}{3}\right){\left(\frac{d\theta }{dt}\right)}^2+g\cos \theta \end{array}}$

Para la posición final, θ=π/2

>> vf=sqrt(9.8*(cos(th_0)-cos(th_0)^3/9)/(L/3)) %velocidad final
vf =    4.8311

Paredes con rozamiento

El extremo B de la escalera permanece en contacto con la pared vertical

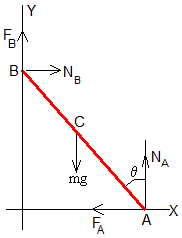
Si el ángulo inicial θ₀ que forma la escalera con la dirección vertical es mayor que el límite, θ₀>θ_s la escalera empieza a deslizar. Las fuerzas de rozamiento F_A y F_B disminuyen ligeramente, ya que el coeficiente cinético μ_k suele ser menor que el estático μ_s

Cuando la escalera desliza, las fuerzas de rozamiento valen, F_A=μ_A·N_A y F_B=μ_B·N_B

En el apartado anterior ya hemos calculado, el vector posición, velocidad y aceleración del centro de masas en términos del ángulo θ

La dinámica de la escalera se describe mediante dos ecuaciones:

• La ecuación del movimiento de traslación del centro de masas
• La ecuación de la dinámica de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas C

${\displaystyle \begin{array}{l}m{\overrightarrow{a}}_c=\left(N_B-F_A\right)\widehat{i}+\left(N_A+F_B-mg\right)\widehat{j}\\ \{\begin{array}{l}{N}_B-{\mu }_A{N}_A=m\frac{l}{2}\left(\cos \theta \frac{d^2\theta }{d{t}^2}-\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\\ N_A+{\mu }_B{N}_B-mg=-m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{d{t}^2}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\end{array}\end{array}}$

Despejamos N_A y N_B del sistema de dos ecuaciones

${\displaystyle \begin{array}{l}{N}_B=\frac{{\mu }_A}{1+{\mu }_A{\mu }_B}mg+\frac{1}{1+{\mu }_A{\mu }_B}m\frac{l}{2}\left\{\left(\cos \theta -{\mu }_A\sin \theta \right)\frac{d^2\theta }{d{t}^2}-\left(\sin \theta +{\mu }_A\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2\right\}\\ N_A=\frac{1}{1+{\mu }_A{\mu }_B}mg-\frac{1}{1+{\mu }_A{\mu }_B}m\frac{l}{2}\left\{\left(\sin \theta +{\mu }_B\cos \theta \right)\frac{d^2\theta }{d{t}^2}+\left(\cos \theta -{\mu }_B\sin \theta \right){\left(\frac{d\theta }{dt}\right)}^2\right\}\end{array}}$

La ecuación de la dinámica de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas C es

${\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=\left(N_A-F_B\right)\frac{l}{2}\sin \theta -\left(F_A+N_B\right)\frac{l}{2}\cos \theta \\ \frac{1}{12}m{l}^2\frac{d^2\theta }{d{t}^2}=\left(N_A-{\mu }_B{N}_B\right)\frac{l}{2}\sin \theta -\left({\mu }_A{N}_A+N_B\right)\frac{l}{2}\cos \theta \end{array}}$

Introduciendo las expresiones de N_A y N_B, despejamos d²θ/dt²

${\displaystyle \begin{array}{l}\left\{\frac{1}{3}+\frac{1}{1+{\mu }_A{\mu }_B}\left(1-{\mu }_A{\mu }_B+2\left({\mu }_B-{\mu }_A\right)\sin \theta \cos \theta \right)\right\}\frac{d^2\theta }{d{t}^2}=\\ 2\frac{g}{l}\frac{1}{1+{\mu }_A{\mu }_B}\left(\left(1-{\mu }_A{\mu }_B\right)\sin \theta -2{\mu }_A\cos \theta \right)+\frac{2}{1+{\mu }_A{\mu }_B}\left({\mu }_A{\cos }^2\theta +{\mu }_B{\sin }^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0. Se suelta la escalera cuando forma un ángulo θ₀>θ_s con la dirección vertical

Equilibrio

Cuando la escalera está en reposo a punto de empezar a deslizar, dθ/dt=0 y d²θ/dt²=0

${\displaystyle \begin{array}{l}\left(1-{\mu }_A{\mu }_B\right)\sin {\theta }_s-2{\mu }_A\cos {\theta }_s=0\\ \tan {\theta }_s=\frac{2{\mu }_A}{1-{\mu }_A{\mu }_B}\end{array}}$

Coeficientes iguales

En el caso de que los coeficientes de rozamiento sean iguales, μ_A=μ_B=μ, las expresiones de N_A, N_B y d²θ/dt², se reducen notablemente

${\displaystyle \begin{array}{l}{N}_B=\frac{\mu }{1+{\mu }^2}mg+\frac{1}{1+{\mu }^2}m\frac{l}{2}\left\{\left(\cos \theta -\mu \sin \theta \right)\frac{d^2\theta }{d{t}^2}-\left(\sin \theta +\mu \cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2\right\}\\ N_A=\frac{1}{1+{\mu }^2}mg-\frac{1}{1+{\mu }^2}m\frac{l}{2}\left\{\left(\sin \theta +\mu \cos \theta \right)\frac{d^2\theta }{d{t}^2}+\left(\cos \theta -\mu \sin \theta \right){\left(\frac{d\theta }{dt}\right)}^2\right\}\\ \frac{d^2\theta }{d{t}^2}=\frac{3}{2-{\mu }^2}\left\{\frac{g}{l}\left(\left(1-{\mu }^2\right)\sin \theta -2\mu \cos \theta \right)+\mu {\left(\frac{d\theta }{dt}\right)}^2\right\}\end{array}}$

El ángulo θ va creciendo a medida que la escalera va cayendo, hasta que la reacción N_B se hace cero, cuando el extremo B deja de estar en contacto con la pared vertical.

Sea una escalera de longitud l=1 m, los coeficientes de rozamiento son iguales μ_A=μ_B=μ=0.3. El ángulo de equilibrio, tanθ_s=2μ/(1-μ²), es 0.58 (33.4°). Soltamos la escalera dθ/dt=0, cuando forma un ángulo θ₀=35°, θ₀>θ_s, resolvemos la ecuación diferencial utilizando la función ode45 de MATLAB y representamos N_B en función del ángulo θ

L=1; %longitud de la escalera+
mu=0.3; %empieza a deslizar con 33.4º
th_0=35*pi/180; %ángulo inicial

f=@(t,x) [x(2);3*(9.8*((1-mu^2)*sin(x(1))-2*mu*cos(x(1)))/L+mu*x(2)^2)/(2-mu^2)]; 
[t,x]=ode45(f,[0,1],[th_0,0]);
acel=3*(9.8*((1-mu^2)*sin(x(:,1))-2*mu*cos(x(:,1)))/L+mu*x(:,2).^2)/(2-mu^2);
N_B=mu*9.8/(1+mu^2)+L*((cos(x(:,1))-mu*sin(x(:,1))).*acel-(sin(x(:,1))+
mu*cos(x(:,1))).*x(:,2).^2)/(2*(1+mu^2));
plot(x(:,1), N_B);
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
ylabel('N_B')
xlabel('\theta')
title('Escalera, con rozamiento')

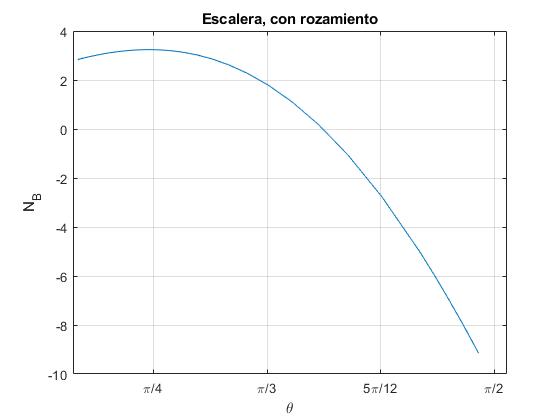
La reacción en el extremo B, N_B se anula para un ángulo θ_l cercano a 1.16 (66°)

El extremo B de la escalera deja de estar en contacto con la pared vertical

La dinámica de la escalera se describe mediante dos ecuaciones:

• La ecuación del movimiento de traslación del centro de masas
• La ecuación de la dinámica de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas C

Siguiendo los mismos pasos que en el apartado anterior, la ecuación del movimiento de traslación del centro de masas es

${\displaystyle \begin{array}{l}m{\overrightarrow{a}}_c=-F_A\widehat{i}+\left(N_A-mg\right)\widehat{j}\{\begin{array}{l}m\frac{d^{2}x}{d{t}^2}-=-{\mu }_A{N}_A\\ -m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{dt}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)=N_A-mg\end{array}\\ \frac{d^{2}x}{d{t}^2}=-{\mu }_{A}g+{\mu }_A\frac{l}{2}\left\{\sin \theta \frac{d^2\theta }{d{t}^2}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right\}\end{array}}$

La ecuación de la dinámica de rotación alrededor de de un eje perpendicular al plano de la escalera que pasa por el centro de masas C es

${\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=N_A\frac{l}{2}\sin \theta -F_A\frac{l}{2}\cos \theta \\ \frac{1}{12}m{l}^2\frac{d^2\theta }{d{t}^2}=N_A\frac{l}{2}\left(\sin \theta -{\mu }_A\cos \theta \right)\\ \frac{1}{12}m{l}^2\frac{d^2\theta }{d{t}^2}=\left\{mg-m\frac{l}{2}\left(\sin \theta \frac{d^2\theta }{dt}+\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\right\}\frac{l}{2}\left(\sin \theta -{\mu }_A\cos \theta \right)\\ \left\{\frac{1}{3}+\left(\sin \theta -{\mu }_A\cos \theta \right)\sin \theta \right\}\frac{d^2\theta }{d{t}^2}=\left(\sin \theta -{\mu }_A\cos \theta \right)\left(2\frac{g}{l}-\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)\end{array}}$

Movimiento completo

El movimiento de la escalera desde la posición inicial θ₀ hasta la posición final π/2, se describe mediante ecuaciones diferenciales de segundo orden:

• la primera, en el intervalo (θ₀, θ_l)

${\displaystyle \frac{d^2\theta }{d{t}^2}=f\left(\theta ,\frac{d\theta }{dt}\right)}$

• la segunda, en el intervalo (θ_l, π/2)

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=f\left(\theta ,\frac{d\theta }{dt}\right)\\ \frac{d^2\theta }{d{t}^2}=g\left(\theta ,\frac{d\theta }{dt}\right)\end{array}}$

Definimos dos funciones: una función que detenga el primer proceso de integración cuando se alcance el ángulo θ_l y de comienzo al segundo proceso de integración y otra que detenga la integración para el ángulo π/2

function [value,isterminal,direction]=stop_escalera_2(t,x, mu, L)
    acel=3*(9.8*((1-mu^2)*sin(x(1))-2*mu*cos(x(1)))/L+mu*x(2)^2)/(2-mu^2);
    N_B=mu*9.8/(1+mu^2)+L*((cos(x(1))-mu*sin(x(1)))*acel-(sin(x(1))+
mu*cos(x(1)))*x(2)^2)/(2*(1+mu^2));
    value=N_B;  
    isterminal=1;
    direction=-1; 
end

function [value,isterminal,direction]=stop_escalera_1(t,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

Consideremos una escalera de longitud l=1, que se suelta cuando forma un ángulo θ₀=35° con la vertical. Representamos el ángulo θ que hace la escalera con la dirección vertical en función del tiempo t

L=1; %longitud de la escalera+
mu=0.3; %empieza a deslizar con 33.4º
th_0=35*pi/180; %ángulo inicial

f=@(t,x) [x(2);3*(9.8*((1-mu^2)*sin(x(1))-2*mu*cos(x(1)))/L+mu*x(2)^2)/(2-mu^2)]; 
opts=odeset('events',@(t,x) stop_escalera_2(t,x, mu,L));
[t,x]=ode45(f,[0,10],[th_0,0],opts);
hold on
plot(t,x(:,1));
tL=t(end); %instante NB=0 
disp([tL,x(end,1)*180/pi])

opts=odeset('events',@stop_escalera_1);
f=@(t,x) [x(2);(sin(x(1))-mu*cos(x(1)))*(2*9.8/L-cos(x(1))*x(2)^2)/(1/3+(sin(x(1))
-mu*cos(x(1)))*sin(x(1)))]; 
[t,x]=ode45(f,[0,10],[x(end,1),x(end,2)],opts);
plot(t+tL,x(:,1))

hold off
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('t')
ylabel('\theta')
title('Escalera, con rozamiento')

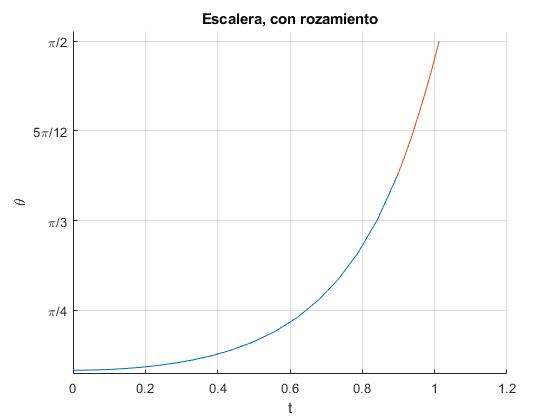
La primera etapa del movimiento se representa en color azul, la segunda, cuando la escalera ya no se apoya en la pared vertical, en rojo. El instante t_l y el ángulo θ_l son

    0.8961   67.4112

Actividades

Se introduce

• El ángulo θ₀ que forma la escalera con la vertical, en el control titulado Ángulo
• El coeficiente de rozamiento μ_s=μ_k=μ, en el control titulado Coef. rozamiento.
• Se han fijado la longitud de la escalera en L=1 m y la masa m=1 kg

Se pulsa el botón titulado Nuevo

El programa interactivo nos suministra los datos del tiempo t, el ángulo θ que forma la escalera con la dirección vertical, las reacciones N_B en el apoyo B en la pared vertical y N_A en el apoyo A en el suelo

Si el ángulo θ₀ es menor que el ángulo límite tanθ_s=2μ/(1-μ²), el programa interactivo nos invita a disminuir el coeficiente de rozamiento o a aumenta el ángulo inicial

Cuando la escalera empieza a deslizar, nos fijaremos en la reacción N_B en el apoyo B con la pared vertical, actuando en el botón paso a paso >| medimos el instante t_l y el ángulo θ_l en el que N_B=0, la escalera deja de estar en contacto con la pared vertical.

Referencias

Yehuda Salu. Revisiting the Ladder on the Wall Problem. The Physics Teacher 49, May 2011, 289-290

Sebastian Glane, Wolfgang H. Müller. The sliding ladder problem revisited in phase space. Am. J. Phys. 87 (6) June 2019, 444-448

Sebastian Glane. Combining dynamics and numerics using the falling ladder problem. Eur. J. Phys. 40 (2019) 055001