Dinámica de una partícula unida a una goma elástica

Supongamos una goma de longitud d sujeta por su extremo superior, del extremo inferior se puede colgar un cuerpo de masa m. El comportamiento de la goma es distinto al de un muelle elástico tal como observamos en la figura.

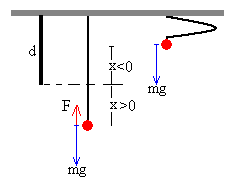
Para x<0 la goma no ejerce ninguna fuerza sobre el cuerpo de masa m. F=0
Para x>0 la goma ejerce una fuerza F=-k·x. Suponiendo que la goma tiene un comportamiento lineal (ley de Hooke)

Si sujetamos el cuerpo con la mano y hacemos que descienda muy despacio. Llega un momento en el que la fuerza que ejerce la goma equilibra el peso del cuerpo y la acción de la mano ya no es necesaria. En esta situación de equilibrio, el cuerpo se ha desplazado x_e

mg=kx_e

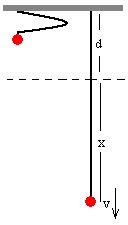
Si se deja caer un cuerpo desde la posición del extremo superior de la goma x=-d, aplicando el principio de conservación de la energía, calculamos la velocidad que alcanza cuando la goma se ha estirado una longitud x.

$\frac{1}{2} m v^{2} + \frac{1}{2} k x^{2} = m g (d + x)$

La máxima deformación x_m de la goma se alcanza cuando v=0

$\frac{1}{2} k x_{m}^{2} = m g (d + x_{m})$

A continuación, describiremos las distintas etapas del movimiento de un cuerpo unido a una goma elástica inicialmente estirada, y que presenta una mayor riqueza de comportamientos que la equivalente de un cuerpo unido a un muelle elástico.

Oscilaciones

Un cuerpo de masa m unido a un muelle elástico de constante k describe un Movimiento Armónico Simple, cuya amplitud es independiente del periodo y cuya frecuencia angular es ω²=k/m.

Supongamos que el cuerpo de masa m se desplaza hacia abajo una longitud z₀ desde la posición de equilibrio y luego se suelta (v=0), tal como se indica en la figura.

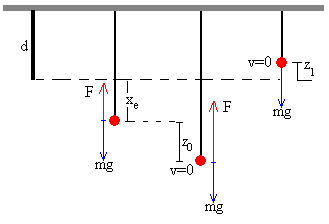
El cuerpo ascenderá impulsado por la fuerza -kx+mg. La ecuación del movimiento se escribirá

$\frac{d^{2} x}{d t^{2}} + \frac{k}{m} x = g$

La solución de esta ecuación diferencial como puede comprobarse por simple sustitución es

x=x_e +Asin(ωt)+Bcos(ωt) con ω²=k/m

Donde x_e=mg/k es la posición de equilibrio, y las constantes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, x=z₀, v=dx/dt=0

La posición x del cuerpo en función del tiempo t será

x=x_e+z₀·cos(ωt)

Pueden ocurrir dos casos:

Si z₀≤x_e

El sistema describe un Movimiento Armónico Simple de amplitud z₀ y de periodo 2π/ω. El periodo de la oscilación es independiente de la amplitud z₀.

Si z₀>x_e

En el instante t=P el cuerpo llega a la posición x=0

$P = \frac{1}{ω} \arccos (- \frac{x_{e}}{z_{0}})$

con velocidad

$v_{0} = - z ω \sin (ω P) = - ω \sqrt{z_{0}^{2} - x_{e}^{2}}$

A partir de este instante, la fuerza que actúa sobre el cuerpo es su propio peso. La máxima altura que alcanza es

$z_{1} = \frac{v_{0}^{2}}{2 g}$

empleando un tiempo de Q=v₀/g

El cuerpo inicia su movimiento descendente, llegando en el instante t=P+2Q a x=0 con velocidad v₀, pero en sentido opuesto. A partir de este momento, actúa la fuerza que ejerce la goma. En el instante t= 2P+2Q vuelve a la posición de partida completándose la oscilación, cuyo periodo vale

$2 P + 2 Q = \frac{2}{ω} \arccos (- \frac{x_{e}}{z_{0}}) + \frac{2 ω}{g} \sqrt{z_{0}^{2} - x_{e}^{2}}$

La amplitud de la oscilación es

$\frac{z_{1} + x_{e} + z_{0}}{2} = \frac{1}{4 x_{e}} {(z_{0} + x_{e})}^{2}$

Aplicando el principio de conservación de la energía, calculamos z₁

$\begin{array}{l} m g (z_{1} + x_{e} + z_{0}) = \frac{1}{2} k {(z_{0} + x_{e})}^{2} \\ z_{1} = \frac{k}{2 m g} {(x_{e} + z_{0})}^{2} - x_{e} - z_{0} = \frac{1}{2 x_{e}} {(x_{e} + z_{0})}^{2} - x_{e} - z_{0} \end{array}$

Conocido z₁ se calcula la amplitud de la oscilación (z₁+x_e+z₀)/2

Ejemplo:

Para k=400 N/m y m=350 kg.

La posición de equilibrio x_ees

$x_{e} = \frac{m g}{k} = \frac{300 \cdot 9.8}{400} = 7.35 m$

Sea la posición de partida z₀ =12.65 m (segundo caso) en el instante t=0 por debajo de la posición de equilibrio.

Empleando el principio de conservación de la emergía calculamos z₁=7.21 m la altura que se eleva el cuerpo en la región x<0.

Calculamos la frecuencia angular ω=1.15 rad/s, y el periodo de la oscilación 6.22 s que como vemos es distinto de 2π/ω, debido a que el cuerpo se mueve en la región x<0 donde la fuerza que ejerce la goma es F=0.

El problema general

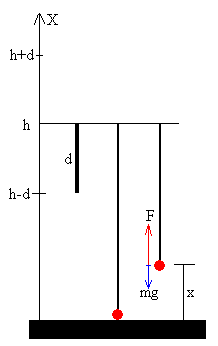
Consideremos una goma elástica de longitud d sin deformar y de constante elástica k (a la izquierda en la figura). Uno de los extremos se sujeta a un poste de altura h. Del extremo libre cuelga un cuerpo de masa m inicialmente anclado a la base del poste tal como apreciamos en la figura (en el centro). Para describir el movimiento unidimensional establecemos el origen en la base del poste y el eje X tal como se indica en la figura

Una vez que se suelta el cuerpo, estudiaremos las distintas etapas de su movimiento hasta que regresa a la base del poste. Supondremos que la goma es perfectamente elástica y que el rozamiento del cuerpo con el aire es despreciable.

Situación inicial

El cuerpo de masa m está sujeto en x=0. La goma está estirada una longitud h-d. La energía inicial es

$E = \frac{1}{2} k {(h - d)}^{2}$

Primera etapa (x<h-d)

Si la fuerza que ejerce la goma k(h-d) es mayor que el peso mg, el cuerpo se eleva, su aceleración es

ma=k(h-d-x)-mg

donde h-d-x es la deformación de la goma cuando el cuerpo se ha elevado una altura x sobre el suelo (a la derecha en la figura).

Tenemos la ecuación diferencial de un M.A.S.

$\frac{d^{2} x}{d t^{2}} + \frac{k}{m} (- h + d + x) + g = 0$

de frecuencia angular ω²=k/m.

La solución de la ecuación diferencial tiene la forma

x=x₀+Asin(ωt)+Bcos(ωt)

con x₀=h-d-g/ω².

Las condiciones iniciales t=0, x=0, v=dx/dt=0 determinan los valores de las constantes A y B. El resultado final es

x=x₀(1-cos(ωt))
v=x₀ω·sin(ωt)

El cuerpo llega a la posición x=h-d, en el instante t₁ tal que

$\frac{- g}{ω^{2}} = x_{0} \cos (ω t_{1})$

con una velocidad v₁

v₁=x₀ω·sin(ωt₁)

Esta velocidad se puede obtener aplicando el principio de conservación de la energía

$\frac{1}{2} k {(h - d)}^{2} = \frac{1}{2} m v_{1}^{2} + m g (h - d)$

Segunda etapa (h-d<x<h+d)

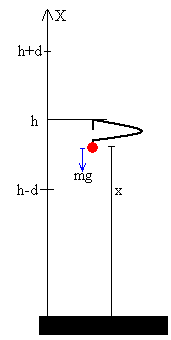
Cuando el cuerpo se encuentra en el intervalo que va desde x=h-d a x=h+d, la goma se dobla pero no se comprime, por tanto, no ejerce ninguna fuerza sobre el cuerpo de masa m. La única fuerza que actúa sobre el cuerpo es su propio peso mg.

La posición y la velocidad del cuerpo en el instante t>t₁ se obtienen a partir de las ecuaciones del movimiento rectilíneo uniformemente acelerado

$\begin{array}{l} v = v_{1} - g (t - t_{1}) \\ x = (h - d) + v_{1} (t - t_{1}) - \frac{1}{2} g {(t - t_{1})}^{2} \end{array}$

El cuerpo llega a la posición x=h+d en el instante t₂ tal que

$2 d = v_{1} (t_{2} - t_{1}) - \frac{1}{2} g {(t_{2} - t_{1})}^{2}$

La velocidad v₂ del móvil será

v₂=v₁-g(t₂-t₁)

Aplicando el principio de conservación de la energía obtenemos v₂ a partir de v₁

$\frac{1}{2} m v_{1}^{2} = \frac{1}{2} m v_{2}^{2} + m g \cdot 2 d$

Dicha velocidad se alcanza en el instante

$t_{2} = t_{1} + \frac{v_{1} - v_{2}}{g}$

Tercera etapa (x>h+d)

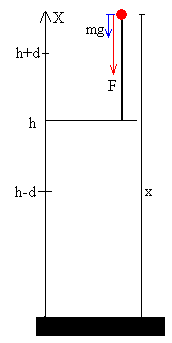
Cuando el cuerpo está a una altura x>h+d, la goma vuelve a estirarse ejerciendo una fuerza sobre el cuerpo cuyo valor es k(x-h-d). La aceleración del cuerpo es

ma= -k(x-h-d)-mg

La ecuación del movimiento se escribe

$\frac{d^{2} x}{d t^{2}} + \frac{k}{m} (- h - d + x) + g = 0$

La solución de la ecuación diferencial tiene la forma

$\begin{array}{l} x = x_{0} + A \sin (ω (t - t_{2})) + B \cos (ω (t - t_{2})) \\ x_{0} = h + d - \frac{g}{ω^{2}} \end{array}$

Las condiciones iniciales t=t₂, x=h+d, v=dx/dt=v₂ determinan los valores de las constantes A y B.

$\begin{array}{l} x = x_{0} + \frac{v_{2}}{ω} \sin (ω (t - t_{2})) + \frac{g}{ω^{2}} \cos (ω (t - t_{2})) \\ v = v_{2} \cos (ω (t - t_{2})) - \frac{g}{ω} \sin (ω (t - t_{2})) \end{array}$

La altura máxima se alcanza en el instante t_m tal que v=0

$t_{m} = t_{2} + \frac{1}{ω} \arctan \frac{ω v_{2}}{g}$

Aplicamos el principio de conservación de la energía para obtener la altura máxima x_m.

$\frac{1}{2} k {(h - d)}^{2} = m g x_{m} + \frac{1}{2} k {(x_{m} - h - d)}^{2}$

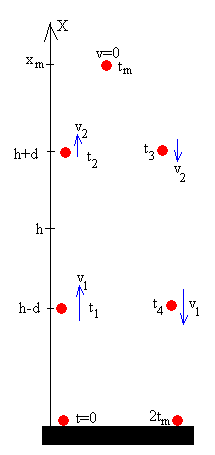
A partir de este instante, se inicia el viaje de vuelta hasta que regresa al punto de partida x=0 con velocidad nula v=0 empleando un tiempo 2t_m.

La posición x=h+d se alcanza en el instante t₃=t_m+t_m-t₂=2t_m-t₂ con una velocidad –v₂

Cuarta etapa (h-d<x<h+d)

La goma no influye en el movimiento del cuerpo, de modo que las ecuaciones del movimiento son similares a las de la segunda etapa.

La posición y la velocidad del cuerpo en el instante t>t₃ se obtienen a partir de las ecuaciones del movimiento rectilíneo uniformemente acelerado

$\begin{array}{l} v = - v_{2} - g (t - t_{3}) \\ x = (h + d) - v_{2} (t - t_{3}) - \frac{1}{2} g {(t - t_{3})}^{2} \end{array}$

Alcanzando la posición x=h-d en el instante t₄=t₃+(t₂-t₁)=2t_m-t₁ con velocidad –v₁

Quinta etapa (0<x<h-d)

La ecuación del movimiento es la misma que en la primera etapa.

La solución de la ecuación diferencial tiene la forma

$\begin{array}{l} x = x_{0} + A \sin (ω t) + B \cos (ω t) \\ x_{0} = h - d - \frac{g}{ω^{2}} \end{array}$

Las condiciones iniciales t=t₄, x=h-d, v=dx/dt=-v₁ determinan los valores de las constantes A y B. El resultado final es

$\begin{array}{l} x = x_{0} - \frac{v_{1}}{ω} \sin (ω (t - t_{4})) + \frac{g}{ω^{2}} \cos (ω (t - t_{4})) \\ v = - v_{1} \cos (ω (t - t_{4})) - \frac{g}{ω} \sin (ω (t - t_{4})) \end{array}$

Alcanzándose la posición x=0 en el instante 2t_m con velocidad v=0. Con lo que se completa un ciclo del movimiento.

Casos particulares

El cuerpo pasa por la posición x=h-d, pero no alcanza la posición x=h+d

Si la energía del cuerpo

$m g (h - d) \leq \frac{1}{2} k {(h - d)}^{2} \leq m g (h + d)$

El cuerpo pasa por la posición x=h-d con una velocidad v₁ empleando un tiempo t₁, calculado en la primera etapa.

El cuerpo alcanza después una altura máxima x_m<h+d

$\frac{1}{2} k {(h - d)}^{2} = m g x_{m}$

en el instante t_m=t₁+v₁/g

El cuerpo después de pasar la posición x=h-d en el camino de vuelta regresa al origen x=0 en el instante 2t_m

No se alcanza la posición x=h-d

Si la energía del cuerpo

$\frac{1}{2} k {(h - d)}^{2} \leq m g (h - d)$

El cuerpo alcanza una altura máxima x_m<h-d que se calcula aplicando el principio de conservación de la energía o poniendo v=0 en la ecuación del movimiento de la partícula en la primera etapa

$\frac{1}{2} k {(h - d)}^{2} = m g x_{m} + \frac{1}{2} k {(h - d - x_{m})}^{2}$

Describiendo un MAS alrededor de la posición de equilibrio x₀=x_m/2. La posición de equilibrio se calcula poniendo a=0, en la primera etapa del movimiento, o bien, k(h-d-x₀)=mg, resultando x₀=h-d-g/ω².

El periodo de la oscilación es 2π/ω, o tiempo que tarda en salir de x=0, y regresar a la misma posición.

Ejemplos

Ejemplo1

Sea k=960.0 N/m y m=300 kg.

El cuadrado de la frecuencia angular es ω²=960/300=3.2 rad²/s²

x=h-d=20 m

El instante t₁ que tarda la partícula en alcanzar la posición x= 20 m es

$- \frac{g}{ω^{2}} = x_{0} \cos (ω t_{1}) x_{0} = h - d - \frac{g}{ω^{2}}$

Despejando t₁ se obtiene t₁=0.98 s

La velocidad v₁=x₀ω·sin(ωt₁)=29.80 m/s

x=h+d=40 m

Aplicando el principio de conservación de la energía calculamos la velocidad v₂

$\frac{1}{2} m v_{1}^{2} = \frac{1}{2} m v_{2}^{2} + m g \cdot 2 d$

v₂=22.27 m/s

El tiempo que tarda en alcanzar esta posición es t₂=t₁+(v₁-v₂)/g=1.75 s

La máxima altura

Aplicando el principio de conservación de la energía calculamos la máxima altura x_m

$\frac{1}{2} k {(h - d)}^{2} = m g x_{m} + \frac{1}{2} k {(x_{m} - h - d)}^{2}$

x_m=49,76 m

El tiempo que tarda en alcanzar esta altura se calcula mediante la fórmula

$t_{m} = t_{2} + \frac{1}{ω} \arctan \frac{ω v_{2}}{g}$

t_m=2.49 s

El tiempo total que tarda en regresar al origen será de 2t_m=4.98 s.

Ejemplo 2

Sea k=360.0 N/m y m=300 kg.

El cuadrado de la frecuencia angular es ω²=360/300=1.2 rad²/s²

Estamos en el caso particular 1

$m g (h - d) \leq \frac{1}{2} k {(h - d)}^{2} \leq m g (h + d)$

x=h-d=20 m

El instante t₁ que tarda la partícula en alcanzar la posición x= 20 m es (primera etapa)

t₁=2.12 s. Alcanzándose la velocidad v₁= 9.38 m/s

La altura máxima se calcula aplicando el principio de conservación de la energía

$\frac{1}{2} k {(h - d)}^{2} = m g x_{m}$

x_m=24.50 m, tardando un tiempo t_m=t₁+v₁/g=3.08 s

El tiempo total que tarda en regresar al origen será de 2t_m=6.16 s.

Ejemplo 3

Sea k=360.0 N/m y m=500 kg.

El cuadrado de la frecuencia angular es ω²=360/500=0.72 rad²/s²

Estamos en el caso particular 2

$\frac{1}{2} k {(h - d)}^{2} \leq m g (h - d)$

Aplicando el principio de conservación de la energía determinamos la altura máxima x_m

$\frac{1}{2} k {(h - d)}^{2} = m g x_{m} + \frac{1}{2} k {(h - d - x_{m})}^{2}$

x_m=12.78 m

El tiempo que tarda en regresar al origen x=0 es el periodo de la oscilación 2π/ω=7.40 s

La oscilación se realiza alrededor de la posición de equilibrio x₀=x_m/2=6.39 m.

k=960; %constante elástica
m=300; %masa
w=sqrt(k/m);
h=30; %altura del poste
d=10; %longitud de la goma sin deformar
%fin de la primera fase
if w^2*(h-d)≤9.8   %el peso es mayor que la fuerza de la goma
        disp('Disminuir la masa o aumentar la constante');
        return;
end

t1=acos(-9.8/(h*w^2-d*w^2-9.8))/w;
v1=(h-d-9.8/w^2)*w*sin(w*t1);
if w^2*(h-d)≤2*9.8   %no se alcanza la posición y=h-d
    t1=pi/w;
    t4=t1;
elseif w^2*(h-d)^2≤2*9.8*(h+d) %no se alcanza la posición y=h+d
     t4=t1+2*v1/9.8;
else       %completa todos los pasos
    v2=sqrt(v1^2-4*9.8*d);
    t2=t1+(v1-v2)/9.8;
%tercera fase (altura máxima y tiempo)
    tMax=t2+atan(w*v2/9.8)/w;
    t3=2*tMax-t2;
    t4=t3+t2-t1;
end 

tt=linspace(0,t4+t1,300); %el periodo es t4+t1
y=zeros(1,length(tt));
v=zeros(1,length(tt));
a=zeros(1,length(tt));
opcion=0;
i=0;
for t=tt
    i=i+1;
    switch opcion
        case 0
            y(i)=(h-d-9.8/w^2)*(1.0-cos(w*t));
            v(i)=w*(h-d-9.8/w^2)*sin(w*t);
            a(i)=w^2*(h-y(i)-d)-9.8;
            if y(i)>h-d
                opcion=1;
            end           
        case 1
            y(i)=(h-d)+v1*(t-t1)-4.9*(t-t1).^2;
            v(i)=v1-9.8*(t-t1);
            a(i)=-9.8;
            if y(i)>h+d
                opcion=2;
            end
            if y(i)<h-d 
                opcion=4;
            end         
        case 2
            y(i)=(h+d-9.8/w^2)+(v2/w)*sin(w*(t-t2))+(9.8/w^2)*cos(w*(t-t2));
            v(i)=v2*cos(w*(t-t2))-(9.8/w)*sin(w*(t-t2));
            a(i)=w^2*(y(i)-h-d)-9.8;
            if y(i)<h+d
                opcion=3;
            end            
        case 3
            y(i)=(h+d)-v2*(t-t3)-4.9*(t-t3).^2;
            v(i)=-v2-9.8*(t-t3);
            a(i)=-9.8;
            if y(i)<h-d
                opcion=4;
            end           
        case 4
            y(i)=(h-d-9.8/w^2)-(v1/w)*sin(w*(t-t4))+(9.8/w^2)*cos(w*(t-t4));
            v(i)=-v1*cos(w*(t-t4))-(9.8/w)*sin(w*(t-t4));
            a(i)=w^2*(h-y(i)-d)-9.8;
            if y(i)>h-d
                opcion=1;
            end        
    end
end
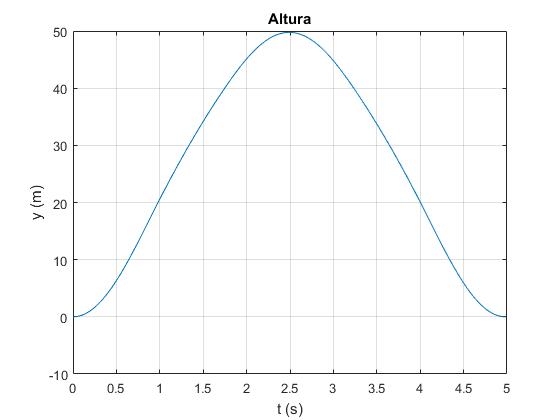
plot(tt,y);
grid on
xlabel('t (s)')
ylabel('y (m)')
title('Altura')

figure 
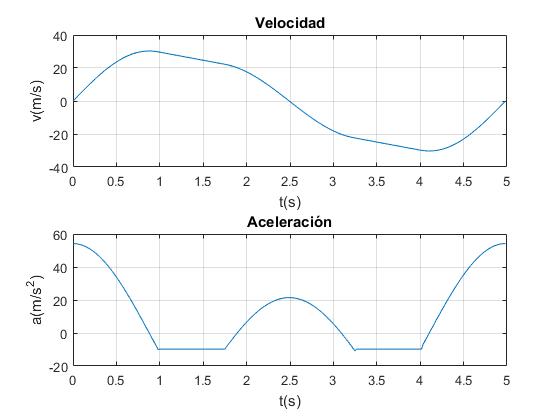
subplot(2,1,1)
plot(tt,v)
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')

subplot(2,1,2)
plot(tt,a)
grid on
xlabel('t(s)')
ylabel('a(m/s^2)')
title('Aceleración')

Actividades

Se introduce

La constante elástica k de la goma, en el control titulado Constante k
La masa m del cuerpo, en el control titulado Masa

En el programa se han fijado los datos de

La altura del poste h=30 m
La longitud de la goma sin deformar d=10 m

Se pulsa el botón titulado Nuevo

En el caso que se introduzca datos de m y k tales que k(h-d)≤mg, el cuerpo no puede ascender, el programa no prosigue, se debe disminuir la masa o aumentar la constante elástica para poder continuar.

Se proporcionan los datos de la posición x, la velocidad v y aceleración a del móvil en un instante t

Al lado del cuerpo, se dibujan las fuerzas que actúan sobre el mismo. En la parte derecha, se dibuja un diagrama en forma de tarta que nos muestra como se van transformando las energías, cinética, potencial gravitatoria, y potencial elástica a medida que se mueve la partícula.

Constante (N/m):
Masa (kg):

Referencias

Theron W F D. The dynamics of a bungee rocket. Eur. J. Phys. 23 (2002), pp. 643-650