Secuencia de colisiones elásticas de n partículas
En la página titulada Secuencia de colisiones elásticas (I) , hemos estudiado el papel jugado por la partícula medidora de masa m2 en la secuencia de dos colisiones elásticas entre una partícula de masa m1 y otra de masa m3.
Fijados m1 y m3, la masa de la partícula mediadora m2 que hace que la velocidad v3 de la tercera partícula sea máxima es
Escribimos la media geométrica de la forma alternativa
Secuencia de n colisiones elásticas
En esta página, las partículas mediadoras en vez de tener una masa arbitraria, tienen una masa que forma una progresión geométrica en la que el primer término es m y el último término es M=mαn
Las masas del conjunto de n+1 partículas son
m, mα, mα2, mα3… mαn-1, mαn=M
Todas las partículas están inicialmente en reposo excepto la incidente de masa M.
Consideremos el caso particular de una secuencia de n=4 colisiones entre 5 partículas para generalizar posteriormente para cualquier otro caso.
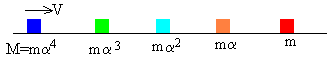
Para obtener la velocidad de las dos partículas después del choque, aplicamos el principio de conservación del momento lineal y la condición de choque elástico, es decir, la suma de la energía cinética de las dos partículas se mantiene constante.
Choque de la primera partícula de masa M=mα4 y la partícula mediadora de masa mα3
Choque de la primera partícula mediadora de masa mα3 y la partícula mediadora de masa mα2
Choque de la segunda partícula mediadora de masa mα2 y la partícula mediadora de masa mα
Choque de la tercera partícula mediadora de masa mα y la partícula final de masa m
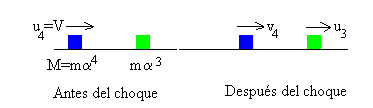
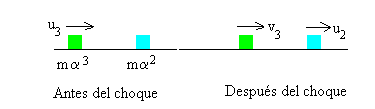
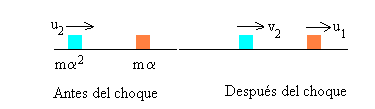
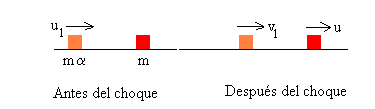
La velocidad de la última partícula de masa m después de la secuencia de cuatro choques es
Téngase en cuenta que M=mα4. En general, para una secuencia de n choques entre n+1 partículas la velocidad final es
Ejemplo
- Masa de la partícula incidente M=25 kg
- Velocidad inicial V=1.0 m/s
- Masa de la última partícula m= 1 kg
- Número de partículas mediadoras entre la primera y última, 3.
Momento lineal inicial: MV=25·1=25 kg·m/s
Energía cinética inicial:
Vamos a determinar como se reparte la energía y el momento lineal entre las partículas después de los choques.
M=25; %Masa de la partícula incidente
m=1; %Masa de la última partícula
n=4; %Número de partículas mediadoras n-1
V=1; %Velocidad inicial
disp('Momento lineal inicial')
M*V
disp('Energía cinética inicial')
M*V^2/2;
alfa=nthroot(M/m,n);
disp('Velocidades después de los choque')
v=((alfa-1)/(alfa+1))*(2*alfa/(alfa+1)).^(0:n-1)*V
u=(2/(alfa+1))^n*(M/m)*V
disp('Momento lineal después de los choque')
p1=(m*alfa.^(n:-1:1)).*v
p2=m*u
disp('Momento lineal total después de los choque')
P=sum(p1)+p2
disp('Energía después de los choques')
E1=(m/2*alfa.^(n:-1:1)).*(v.^2)
E2=m*u^2/2
disp('Energía total después de los choque')
sum(E1)+E2
Momento lineal inicial ans = 25 Energía cinética inicial ans = 12.5000 Velocidades después de los choque v = 0.3820 0.5279 0.7295 1.0081 u = 3.6475 Momento lineal después de los choque p1 = 9.5492 5.9017 3.6475 2.2542 p2 = 3.6475 Momento lineal total después de los choque P = 25.0000 Energía después de los choques E1 = 1.8237 1.5576 1.3304 1.1363 E2 = 6.6519 Energía total después de los choque ans = 12.5000
Recogemos los resultados del cálculo en una tabla
| Partícula | Índice i | Masa mαi | Velocidad después del choque | Momento lineal | Energía cinética |
|---|---|---|---|---|---|
| Incidente | 4 | 25 | 0.382 | 9.549 | 1.824 |
| Mediadora | 3 | 11.18 | 0.528 | 5.902 | 1.558 |
| Mediadora | 2 | 5 | 0.729 | 3.647 | 1.330 |
| Mediadora | 1 | 2.24 | 1.008 | 2.254 | 1.136 |
| Última | 0 | 1 | 3.647 | 3.647 | 6.652 |
| Total | 25.0 | 12.5 |
El momento lineal total de todas estas partículas es
Tenemos la suma de una progresión geométrica cuyo primer término es 1, la razón es 2/(α+1) y n es el número de términos
Energía cinética
Tenemos la suma de una progresión geométrica cuyo primer término es 1, la razón es y n es el número de términos
Secuencia de infinitos choques
Hemos demostrado que, para una secuencia de n choques entre n+1 partículas la velocidad final es
Cuando n es muy grande, es decir, n→∞, calculamos el límite
Hacemos el cambio x=1/n
Aplicamos la regla de l’Hopital
La velocidad final de la última partícula de masa m después de la secuencia de infinitos choques es
Paradoja
El cambio de momento lineal es la diferencia entre le momento lineal inicial y el momento lineal de la última partícula
De mismo modo, el cambio de energía es
Toda la energía cinética de la partícula incidente de masa M y velocidad V ha sido transferida a la última partícula de masa m, a través de una secuencia infinita de choques elásticos.
Actividades
- La velocidad inicial de la primera partícula se ha fijado en V=1 m/s
- La masa de la última partícula se ha fijado en m= 1 kg
Se introduce
- La masa M de la primera partícula, en el control titulado Masa primera.
- El número de partículas mediadoras en el control titulado Número de mediadoras
Se pulsa el botón titulado Nuevo
Se observa la secuencia de choques, los cambios en el momento lineal y la energía cinética de cada una de las partículas del sistema.
Referencias
Bashkansky E. Netzer N. The role of mediation in collisions and related analogs.Am. J. Phys. 74 (12) December 2006, pp. 1083-1087

